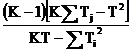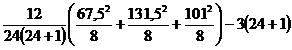METODE
DE COMPARATIE PENTRU ESANTIOANE PERECHI
1.
PROBA COCHRAN
Se utilizeaza cand:
datele sunt sub forma unor semne : +, - (regres, progres)
fata de o valoare la care se face raportarea
sunt K esantioane
nu tine cont de forma distributiei
c2 = 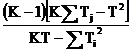
unde:
Tj - totalul semnelor pozitive pe linia i
Tj - totalul semnelor pozitive pe coloana j
T - totalul general
K - numarul de coloane
Nr. grade de libertate:
df = K - 1
PROBLEMA 3 - Proba Cochran
Rezultatele obtinute marcate sub
forma de progres, stagnare, regres sunt rare
2.
PROBA FRIEDMAN
Se utilizeaza cand:
datele nu respecta criteriul de normalitate
avem K masuratori repetate
nu tine cont de forma distributiei
analog ANOVA
c2 = 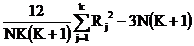
unde: Rj - suma rangurilor pentru conditia
j
N - numarul de subiecti
K - numarul de conditii
df = K - 1 - numarul gradelor de libertate
PROBLEMA 4 - Proba Friedman
echivalent cu analiza de varianta cu un singur factor
design unifactorial pe masurari
repetate
aceasta proba testeaza ipoteza nula care
stipuleaza faptul ca scorul
corespondent fiecarui subiect provine din populatii identice
si este in mod particular sensibil la diferentele tendintei
centrale la nivel de populatie.
Ne propunem sa testam ipoteza conform
careia valoarea calitatii unei conferinte este legata
de cantitatea de suport vizual utilizat.
Se iau in cercetare 17 traineri care fac in mod uzual
prezentari in diverse medii de afaceri.
S-au constituit 3 grupuri de public, diferite dar
echivalente (fiecare subiect are un echivalent in cealalta grupa).
Fiecare trainer prezinta acelasi material la
cele trei grupuri de public - fara suport vizual, cu cateva folii
pentru ilustrarea punctelor esentiale, cu folii si tabele care
sa ilustreze fiecare eveniment al expunerii.
La sfarsitul fiecarei expuneri, publicul trebuie
sa evalueze calitatile expunerii pe o scala de 75 de
puncte. Media evaluarilor tuturor membrilor din grup constituie evaluarea
respectivului training.
datele ar trebui sa fie corelate pentru ca acelasi
trainer prezinta material in cele trei grupe
un scor ridicat reprezinta o evaluare favorabila
Rezultatele obtinute sunt:
|
Suport absent
|
|
Suport redus
|
|
Suport bogat
|
|
1.
|
50
|
(1)
|
|
58
|
(3)
|
|
54
|
(2)
|
|
2.
|
32
|
(2)
|
|
37
|
(3)
|
|
25
|
(1)
|
|
3.
|
60
|
(1)
|
|
70
|
(3)
|
|
63
|
(2)
|
|
4.
|
58
|
(2)
|
|
60
|
(3)
|
|
55
|
(1)
|
|
5.
|
41
|
(1)
|
|
66
|
(3)
|
|
58
|
(2)
|
|
6.
|
36
|
(2)
|
|
40
|
(3)
|
|
28
|
(1)
|
|
7.
|
26
|
(3)
|
|
25
|
(2)
|
|
20
|
(1)
|
|
8.
|
41
|
(1)
|
|
60
|
(3)
|
|
50
|
(2)
|
|
9.
|
72
|
(1)
|
|
73
|
(2)
|
|
75
|
(3)
|
|
10.
|
49
|
(2)
|
|
54
|
(3)
|
|
42
|
(1)
|
|
11.
|
52
|
(2)
|
|
57
|
(3)
|
|
47
|
(1)
|
|
12.
|
36
|
(2)
|
|
42
|
(3)
|
|
29
|
(1)
|
|
13.
|
37
|
(3)
|
|
34
|
(2)
|
|
31
|
(1)
|
|
14.
|
58
|
(3)
|
|
50
|
(1)
|
|
56
|
(2)
|
|
15.
|
39
|
(1)
|
|
48
|
(3)
|
|
44
|
(2)
|
|
16.
|
25
|
(2)
|
|
29
|
(3)
|
|
18
|
(1)
|
|
17.
|
51
|
(1)
|
|
63
|
(2)
|
|
68
|
(3)
|
|
|
30
|
|
|
45
|
|
|
27
|
Daca acceptam ipoteza nula ca
adevarata, atunci ne asteptam ca acest clasament sa
fie distribuit intr-o maniera aleatorie pentru fiecare trainer.
Se poate ca unii traineri sa obtina
rezultate mai slabe fara suport vizual decat intr-o alta
faza a expunerii, atunci cand utilizeaza un suport vizual bogat.
Ne-am astepta ca suma clasamentelor pe fiecare
coloana sa fie aproape egala.
Daca cantitatea de suport vizual
influenteaza calitatea evaluarii trainingului (trainerul este
mai apreciat), ne asteptam ca cea mai mare parte din traineri sa
obtina cea mai mare evaluare in conditiile in care nu
utilizeaza suport vizual.
atribuim ranguri
calculam c2
N=17, K=3
cF2 = 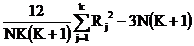
cF2 = 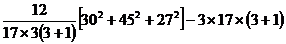
cF2 = 10,94
Calculam nr. gradelor de
libertate
df = K - 1
df = 3 - 1 = 2
|
 p p
|
0,05
|
0,01
|
|
df = 2
|
5,99
|
9,21
|
cH2 =10,94
Interpretare
Intrucat valoarea calculata a
lui c2 care este
10,94 este mai mare decat valoarea critica la pragul de 0,01, care este de
9,21, sansele ipotezei nule sunt mai mici de 1%, ceea ce ne permite
sa respingem ipoteza nula si admitem ipoteza specifica,
care spune ca evaluarea facuta trainerilor difera in
functie de cantitatea de suport utilizata.
Cea mai buna evaluare este in
cazul utilizarii unui suport vizual schematizat.
Aplicatia in programul SPSS 15.0
Dupa ce am parcurs primii pasi in rezolvarea
unei probleme si ne-am decis asupra testului statistic pe care il vom
utiliza vom construi baza de date asa cum apare in ecranele de mai jos.
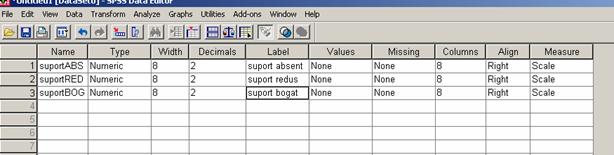
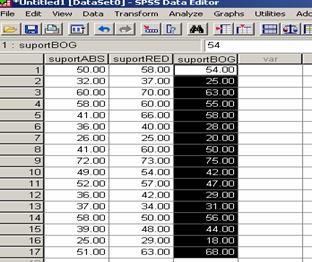
Avem o singura variabila independenta cu trei
modalitati, si tinand cont de faptul ca sunt
masurari repetate vom pune modalitatile variabilei
independente pe coloane, asa cum apare in ecranele de mai sus.
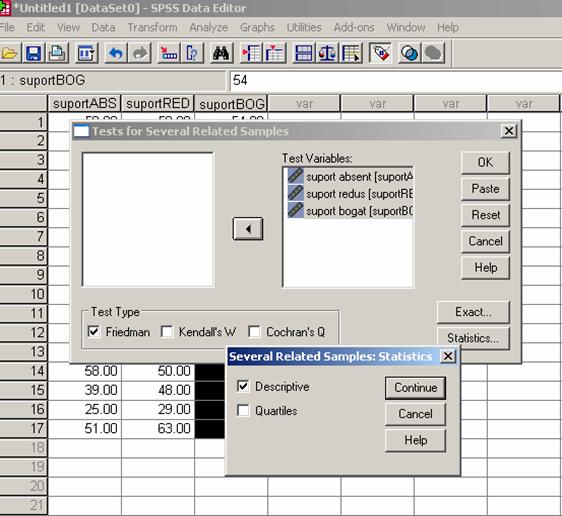
Vom alege de la optiunea Nonparametric
Tests - K Related Samples si vom opta pentru testul Friedman, dupa ce
am plasat modalitatile variabilei independente in cadrul Test
Variables. De asemenea vom alege si de analiza descriptiva.
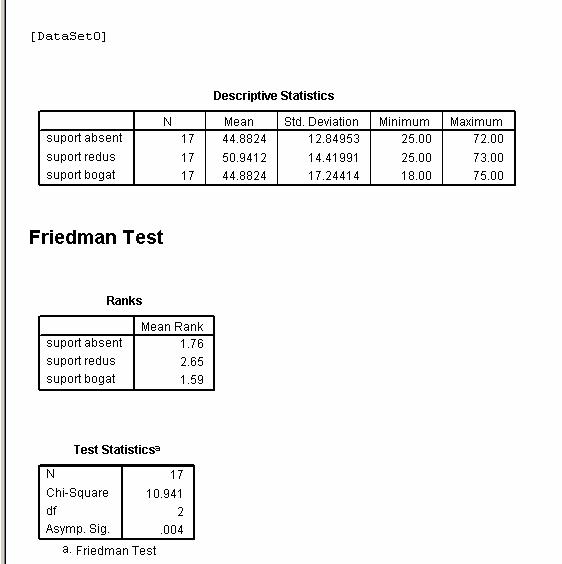
Astfel, obtinem atat calculele descriptive cat
si rezultatele testului Friedman. Prin urmare observam ca
valoarea testului χ ² = 10.941 la un p = .004 mai mic decat pragul critic
de .01 ceea ce ne permite sa afirmam ca sansele ipotezei nule sunt mai mici de 1%, prin urmare respingem ipoteza nula si admitem
ipoteza specifica exista diferente semnificative in ceea
ce priveste ca evaluarea facuta trainerilor difera in
functie de cantitatea de suport utilizata.
Cea mai buna evaluare este in
cazul utilizarii unui suport vizual schematizat.
PASI IN REZOLVAREA
ORICAREI PROBLEME
identificarea variabilei si tipul de design
formularea ipotezelor
verificarea formei distributiei - intocmirea histogramei
se decide cu privire la metoda statistica utilizata
se regrupeaza datele celor K esantioane aplicate
se calculeaza pentru ansamblul datelor mediana teoretica
- pentru proba medianei
(sau se atribuie ranguri)
sistematizarea datelor in tabel (pentru fiecare grup vom vedea
cate valori depasesc mediana teoretica si cate sunt
inferioare acesteia - pentru proba medianei)
(se inlocuiesc rangurile in tabelul cu rezultatele
calculam pe c2
interpretarea datelor
PROBLEME
PROBLEMA 5 - Testul U generalizat
Trei profesori de engleza care tin un curs de
primul nivel revendica fiecare onoarea de a avea cei mai buni elevi.
Pentru a transa chestiunea, opt elevi au fost luati aleator din
fiecare clasa si supusi toti aceluiasi examen,
corectat de un profesor neutru care ignora din ce clasa provin
candidatii (elevii).
Datele sunt urmatoarele:
|
cls. A
|
82
|
71
|
56
|
58
|
63
|
64
|
62
|
53
|
|
cls. B
|
55
|
88
|
85
|
83
|
71
|
70
|
68
|
72
|
|
cls. C
|
65
|
54
|
66
|
68
|
72
|
78
|
65
|
73
|
Ce concluzie se impune? (avem esantioane
independente)
1. Identificarea
variabilelor
VI: A - clasele
a1 - clasa A
a2 - clasa B
a3 - clasa C
VD: X - performanta
Design experimental: de
baza
Tip de esantion - esantioane independente
2. Formularea
ipotezelor
Ipoteza specifica Hs
Exista diferente
semnificative in ceea ce priveste performantele subiectilor in
functie de clasa din care provin
Ipoteza nula (atribuita hazardului)H0:
Diferentele aparute intre
performantele elevilor din diferite clase se datoreaza hazardului
(intamplarii).
3. Verificarea
distributiei -. histograma
distributia nu respecta criteriul de normalitate
(asimetrica - nu sunt nici macar 2 note egale)
optam pentru testul U generalizat (nu sunt multe ranguri
egale)
4. Atribuim
ranguri de la valoarea cea mai mica pana la valoarea cea mai mare:
val. min. = 53
val. max. = 88
|
x
|
53
|
54
|
55
|
56
|
58
|
62
|
63
|
64
|
65
|
66
|
68
|
70
|
71
|
72
|
73
|
78
|
82
|
83
|
85
|
88
|
|
f
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
2
|
1
|
2
|
1
|
2
|
2
|
1
|
1
|
1
|
1
|
1
|
|
|
rang
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
10
9,5
|
1
|
12
13
12,5
|
14
|
15
16
15,5
|
17
18
17,5
|
19
|
20
|
21
|
22
|
23
|
24
|
=nr. total de
subiecti
inlocuim datele cu rangurile in tabelul cu rezultatele
|
Clasa A
|
|
Clasa B
|
|
Clasa C
|
|
X
|
rang
|
|
x
|
rang
|
|
x
|
rang
|
|
82
|
21
|
|
55
|
3
|
|
65
|
9,5
|
|
71
|
15,5
|
|
88
|
24
|
|
54
|
2
|
|
56
|
4
|
|
85
|
23
|
|
66
|
11
|
|
58
|
5
|
|
83
|
22
|
|
68
|
12,5
|
|
63
|
7
|
|
71
|
15,5
|
|
72
|
17,5
|
|
64
|
8
|
|
70
|
14
|
|
78
|
20
|
|
62
|
6
|
|
68
|
12,5
|
|
65
|
9,5
|
|
53
|
1
|
|
72
|
17,5
|
|
73
|
19
|
|
R1=67,5
|
|
|
R2=131,.5
|
|
|
R3=101
|
Calculam suma rangurilor pentru fiecare clasa
N = 24
n1 = 8
n2 = 8
n3 = 8
cH2 = 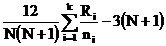
cH2 =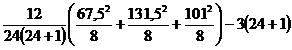
cH2 =
5,123
Calculam nr. gradelor de
libertate
df = K - 1
df = 2
|
P
|
0,05
|
0,01
|
|
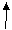 df = 2 df = 2
|
5,99
|
9,21
|
cH2 =10,36
Interpretare
Intrucat valoarea calculata a
lui c2 de
5,123este mai mica decat valoarea critica la pragul de 0,05, care
este 5,99, sansele ipotezei nule sunt mai mari de 5%, suspendam
decizia si dam credit ipotezei nule.
Verificam cu SPSS
|
clasa
|
nota
|
filter
|
|
Histograma - pe rand
Selected cases
apoi alegem din Selected cases: All
Statistics - Nonparametric Tests T
K Independent Samples
Test Variable..: note
Grouping variable: clasa (1,3)
Define Range 1 - min. - 3 - max.
|
|
1.
|
1,00
|
notele pe rand
|
|
|
|
2.
|
2,00
|
|
|
|
|
3.
|
1,00
|
|
|
|
|
4.
|
1,00
|
|
|
|
|
|
|
|
|
|
24.
|
|
|
|
|
Test Statistitc a,b
Chi Square Nota 5,133
a) Kruskal Wallis Test
PROBLEMA 6 - Proba Friedman
O metoda de evaluare a unei institutii de
ocrotire a fost considerata ca fiind numarul de absente
inregistrate la adolescenti delicventi.
Pentru aceasta s-au luat un numar de 12
adolescenti pentru care au fost monitorizate absentele:
a) luna inainte de plasarea
lor in institutie
b) luna perioada cat s-au
aflat in institutie
c) luna dupa ce au
parasit institutia
Datele sunt urmatoarele:
|
Adolescenti
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
inainte
|
10
|
12
|
12
|
19
|
5
|
13
|
20
|
8
|
12
|
10
|
8
|
18
|
|
in timpul
|
5
|
8
|
13
|
10
|
10
|
8
|
16
|
4
|
14
|
3
|
3
|
16
|
|
dupa
|
8
|
7
|
10
|
12
|
8
|
7
|
12
|
5
|
9
|
5
|
3
|
2
|
Aplicati testul Friedmann.
La ce concluzie ajungeti? (esantioane perechi)
|
Inainte
|
|
In timpul
|
|
Dupa
|
|
1.
|
10
|
(3)
|
|
5
|
(1)
|
|
8
|
(2)
|
|
2.
|
12
|
(3)
|
|
8
|
(2)
|
|
7
|
(2)
|
|
3.
|
12
|
(2)
|
|
13
|
(3)
|
|
10
|
(1)
|
|
4.
|
19
|
(3)
|
|
10
|
(1)
|
|
12
|
(2)
|
|
5.
|
5
|
(1)
|
|
10
|
(3)
|
|
8
|
(2)
|
|
6.
|
13
|
(3)
|
|
8
|
(2)
|
|
7
|
(1)
|
|
7.
|
20
|
(3)
|
|
16
|
(2)
|
|
12
|
(1)
|
|
8.
|
8
|
(3)
|
|
4
|
(1)
|
|
5
|
(2)
|
|
9.
|
12
|
(2)
|
|
14
|
(3)
|
|
9
|
(1)
|
|
10.
|
10
|
(3)
|
|
3
|
(1)
|
|
5
|
(2)
|
|
11.
|
8
|
(3)
|
|
3
|
(1,5)
|
|
3
|
(1,5)
|
|
12.
|
18
|
(3)
|
|
16
|
(2)
|
|
2
|
(1)
|
|
|
R1 = 32
|
|
|
R2=22,5
|
|
|
R3=17,5
|
Ipoteza
specifica:
numarul de absente este legat de prezenta in institutie a
adolescentilor
Ipoteza nula: Distribuirea absentelor
pentru fiecare adolescent este aleatorie. Ne asteptam ca suma
rangurilor (pe fiecare coloana) sa fie aproximativ egala.
atribuim ranguri
calculam c2
cF2 = 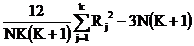
cF2 = 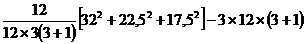
cF2 = 8,4295
Calculam nr. gradelor de
libertate
df = K - 1
df = 3-1 = 2
|
p
|
0,05
|
0,01
|
|
 df = 2 df = 2
|
5,99
|
9,21
|
cH2 =8,4295
Interpretare
Intrucat valoarea calculata a
lui c2 care este
8,4295 este mai mare decat valoarea
critica la pragul de 0,05, care este de 5,99, sansele ipotezei nule
sunt mai mici de 1%, ceea ce ne permite sa respingem ipoteza nula
si admitem ipoteza specifica, care spune ca numarul de
absente al adolescentilor difera in functie de plasarea lor
in institutie.
Cea mai buna evaluare este in
cazul monitorizarii inainte de plasarea lor in institutie.