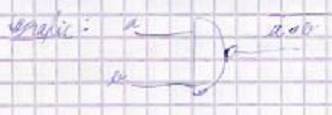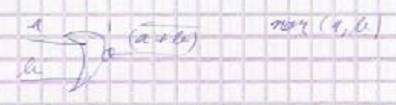PROIECTARE LOGICA
Reprezentarea numerelor reale
-contin o parte
intreaga si o parte fractionala
Real=ąPI.PZ (I.F) Integer Fraction
Exemplu: -
2713.125 FIXED POINT Representation
(=Virgula fixa)
Semn mantissa exponent
Reprezentarea cu
semn,mantissa si exponentul numita reprezentarea in virgula mobila (floating
Point Representation-e mai avantajoasa.
Reprezentarea in
sistem binar a numerelor reale.
Reprezentarea in
virgula mobila.
Fie x= -2713.125
Pas 1 Conversia
binara
Partea
intreaga
Partea
fractionara
10 10 100 11 00 1
x= -0 0| 1010
1001 1001.001
Alg de conversie
a pz
αn-1
αn-2 α0 α-1 α-2
α-K
pf=001
=>00|101010011001.001
schimbam y=
-2713.126
*126=?binar
neconvergent
Nr de pasi ajunge
la ∞ .
Reprezentarea in
virgula flotanta in sistemele de calcul se bazeaza pe urmatoarele conventii:
- nr de biti N=32 FLOAT Simple Precison FLSP
N=64 FLOAT Double Precision FLDP
N=124 FLOAT Extended Precision FLEP
BYTE3 24 32 BYTE2 b15 BYTE1 b8 b7 BYTE0 b0
Sgn 30
B31=Sgn
0,pt +
1 pt -
b23-b30=EXP(8biti)
b0 → b22=MANTISSA
NORMALIZATA (23 biti)
bitul 22 trebuie sa fie
neaparat 1
x= -1010 1001
1001.001 - Fixed point
sgn=1(minus) 1210 =000011002
exp=00001100
Imaginea memorie
este:
1│0000|1100
8 6 5 4 C 9 0 0
b0 b-1
b-2 b-∞
23biti
Err max reprez FL
POINT este1/223 sau gener. err max=1/2m, unde m este nr
de biti pe care se reprez mantissa.
Precizia dubla
mantissa → se prelungeste pe inca un cuv de 32 biti =>n =55 (23+32)
Precizia extinsa →
se acorda inca 64 biti
mantissa ocupa
m=23+64+32=119 biti
Err max=1/255 Emax=1/2119
Err max=1/223~1/8*106~0.125*10-6 ppm=parti per milion=0.125 ppm
Conventii
suplimetare de reprezentare.
exponentul
-pozitiv
negativ
Se reprezinta in C2
Exp in C2
Exp I
[-128,127]
Daca in urma unor operatii suma Exp=
-128 (zecimal) ar fi nr cel mai mic posibil
0 e acel nr care are exp = -128
sau mai mic decat acesta
Exp cu offset de +128:
Reprezentarea 1│0000110010
10 |100 1100 1001 0 0
standard
Exp
8654C90016
Reprezentarea 1│10001100│ 0 10 100 1100 1001 0 0
offset
Exp +128 C654C90016
27
Metoda de
reprezentare cu bit ascuns(hidden bit) → primul bit de dupa exponent este
obligatoriu 1, deci nu se mai scrie in calcule, se adauga.
Inseamna ca am
capatat pe pozitia bitului cel mai
semnificativ un bit in plus.
Operatii cu
numere reale
Adunare intre 2
nr cu acelasi semn si acelasi exponent
x=0,5 exp=0
m=100
y=0,5 exp=0
m=1
x+y
In urma acestui
proces, rezultatul trebuie renormalizat, se obtine depasire.
Procesul de
normalizare necesita op de deplasare a mantisei catre dreapta cu o unitate,
majorarea exponentului cu 1.
Suma 123.5+99.71
ac semn, nu au
ac. exponent
Nr cu exponent
mai mic trebuie deplasat catre dreapta cu atatea pozitii, cu cat arata
diferenta exponentilor (aliniere sau axarea operanzilor).
S-ar putea sa fie
necesara renormalizarea.
Pentru a efectua
adunarea a 2 nr cu acelasi semn, op. necesare ar fi:
Pasul 1:Alinierea
sau axarea celor 2 mantise, daca exponentii sunt diferiti.
In final, daca se
obtine depasire , inseamna ca este necesara normalizarea rez.
x=123.5 si y=3.75
si 123.5+3.75 e necesara axarea.
Adunarea a 2
numere de semne contrare(scadere)
-operatiile
generale in urma operatiunii de adunare scadere efectuate in sistem
→alinierea
operanzilor
→C2(cel
cu - trebuie Complement fata de 2)
→normalizari(aducerea
bitului 1 pe pozitia bitului cel mai semnificativ al mantisei)
Inmultire→suma
exponentilor
val→inmultirea celor 2 mantise
2 variante: - 1.
mantisa ramane normalizata → exponentul se pastreaza
- 2. mantisa trebuie
renormalizata → exponentul se diminueaza
Impartire
x/y=x*1/y
ALGEBRA LOGICA(BINARA)
AL=
Operanzi:-constante
logice: (T,F) (Y,N) (0,1)
-variabile(entitati notate cu
litere sau grupuri de litere): a, ion, α, etc.
aI
Operatori logici:
-operatorul
"unar" NEGATIE
not(1)=0
1'=0 0'=1;1'=0;1''=1
-un nr impar de
negatii complementeaza rezultatul
-un nr par de
negatii intoarce acelasi rezultat
--->
1 0 Poarta logica inversoare
In out
Obs --○►-- 0=negatie
--►--
Operatorul SI
-AND
Simbol: ∙ ,
∩ , Λ, conjunctie, produs logic
x
Grafic =D- x nad y=x*y
y x*y
Operatorul SI da rezultatului
valoare logica 1(true), numai daca toti operanzii implicati au in acelasi
moment valoarea 1(true).
and este un operator numit "minterm"
Rez and Rez or
Operatorul SI
s.n. conjunctie ; produs logic →are un caracter de adevar minimal.
Operatorul SAU -
OR disjunctie; suma logica.
Simbol
α-num: + , U , V , or
Grafic 
Operatorul or
confera rezultatului valoarea 0, numai daca toate variabilele au in acel moment
valoarea 0.
- or este numit
"maxterm"
- and,or au
actiune asupra a 2 sau mai multi biti
O expresie logica
(functie logica) dependenta de mai multe variabile se poate defini prin tabela
de adevar a acesteia, care se reduce la atasarea unei valori logice pt toate
combinatiile posibile a variabilelor care o definesc → tabela de adevar a
expresiei.
Orice functie
logica exprimata prin tabela acesteia de adevar poate fi obtinuta prin utilizarea
celor 3 operatori =>operatori logici fundamentali.
intre 0 si 31 ne
trebuie 5 biti
Sa se scrie
tabela de adevar a unei functii care are valoarea logica 1 atunci cand numarul
se imparte exact la 3 sau la 5 sau care se impart si la 3 si la 5.
0
1 1 1 1 1 0
M(3&5)=X'4*
X'3* X'2* X'1* X'0 + X4'
* X3* X2* X1* X0 + X4 *X3 *X2 *X1*X0'
Din exemplu
rezultatul care se obtine s.n. expresie canonica de tip disjunctiv.
Operatori
nefundamentali →1)not(and)
(operatul and legat)
nand
(a*b)'=not(a*b)
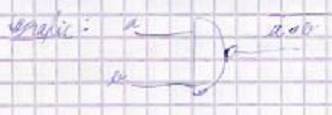
2)nor
(a+b)=not(or) =(or)'
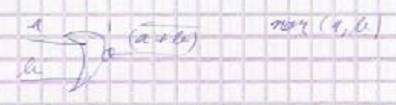
3)sau exclusiv
XOR (opereaza doar pe 2 variabile)
|
a
|
b
|
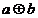
|
|
|
|
|
|
|
|
|
|
|
|
|
Axorb=suma modulo
2
Negatul lui XOR
s.n. concidenta. a=b