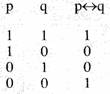Principalele functii de adevar

Principalele functii de adevar

Negatia (simbolizata prin "¬" sau prin "−", "p"). Prin negarea unei propozitii p se obtine o noua propozitie ("non-p"), complementara in raport cu prima, care este adevarata cand p este falsa si falsa cand p este adevarata. Considerand propozitia "Afara ploua", fiecare din formele urmatoare pot fi considerate drept negatia propozitiei initiale: "Afara nu ploua", "Nu ploua afara", " Nu este cazul ca afara ploua", "Este fals ca afara ploua" etc.

Propozitia initiala (p) si negaia ei (¬p) se afla in raport de contradictie, adica nu pot fi simultan nici adevarate, nici false. Cum negatia schimba valoarea de adevar a propozitiei negate, prin dubla negatie a unei propozitii se va obtine propozitia initiala (¬¬p = p).

Conjunctia (simbolizata prin "&" sau prin ,, ") a doua propozitii este adevarata numai daca ambele propozitii (numite si "conjuncte" sau "conjuncti") sunt adevarate. In restul cazurilor, cand cel putin una este falsa, si conjunctia acestora va fi falsa. In limba naturala, conjunctia este semnalata prin expresii de genul: "si", "iar", "desi", "dar", "cu toate ca", "in pofida" etc. Pornind de exemplu de la doua propozitii precum "Afara ploua" si "Eu plec la pescuit", conjunctia acestora poate fi regasita in oricare dintre urmatoarele exprimari ale aceluiasi fapt: "Afara ploua si eu plec la pescuit", "Afara ploua, iar eu plec la pescuit", "Desi afara ploua, eu plec la pescuit" etc.

Daca unul dintre termenii unei conjunctii este fals, atunci intreaga conjunctie va fi falsa (p & 0 = 0), iar daca unul dintre termenii sai este adevarat, valoarea sa de adevar este determinata de valoarea celuilalt termen (p & 1 = p).

Disjunctia (simbolizata prin ,, ") a doua propozitii este adevarata numai daca cel putin una dintre ele este adevarata, si este falsa daca ambele sunt false. In limbajul natural disjunctia este semnalata prin expresii de genul: "sau", "fie", "ori" etc. Aceste expresii lingvistice sunt vagi, in sensul in care uneori pot exprima nu numai o disjunctie inclusiva ( , precum cea a carei valoare de adevar am precizat-o mai inainte, ci si una exclusiva (w), tabelele de adevar ale acestora fiind diferite. In cazul disjunctiei exclusive, este eliminata situatia in care ambele propozitii componente sunt adevarate, caz in care disjunctia este considerata falsa. Acest lucru este exprimat uneori prin dubla aparitie a expresiilor disjunctive de mai inainte. Astfel, expresia "Ma duc la mare sau ma duc la munte" reprezinta o disjunctie inclusiva, caz in care ambele actiuni pot fi indeplinite, in timp ce enuntul "Sau ma duc la mare, sau ma duc la munte" exprima o disjunctie exclusiva. Analog, expresii de tipul "ori, ori", "fie, fie" conduc catre interpretarea unei disjunctii in sens exclusiv.

Daca unul dintre termenii unei disjunctii inclusive este adevarat, atunci intreaga disjunctie va fi adevarata (p 1 = 1), iar daca unul dintre termenii sai este fals, valoarea sa de adevar este determinata de valoarea celuilalt termen (p p).

Disjunctia exclusiva este adevarata cand termenii ei au valori de adevar diferite si este falsa cand au aceeasi valoare de adevar.

   

Implicatia (simbolizata prin "→") reprezinta o relatie de succesiune logica intre doua propozitii si este falsa doar daca prima propozitie a implicatiei este adevarata si cea de-a doua falsa, in restul cazurilor implicatia fiind adevarata. In limbajul natural, implicatia este semnalata prin expresii de genul: "daca atunci", "implica", "din rezulta", "din deducem pe". Astfel, "Daca ploua (p), atunci imi iau umbrela (q)" reprezinta o implicatie, numita si conditional, prima propozitie (p) fiind numita antecedent, iar cea de-a doua (q) consecvent. Se mai spune ca "p" reprezinta o conditie suficienta pentru "q", iar "q" o conditie necesara pentru "p". Astfel se explica de ce implicatia exprima uneori si raportul mai complex al relatiei dintre cauza si efect, antecedentul reprezentand o cauza suficienta pentru producerea efectului, respectiv consecventul. O expresie de tipul "numai daca", "doar daca" etc. reprezinta ceea ce se numeste o implicatie inversa. In acest caz, simbolizarea expresiei din limbajul natural "Numai daca plouä (p), imi iau umbrela (q)" se face prin formula logica "q→p".

Din tabelul de valori al implicatiei deducem urmatoarele legi de reducere a valorii acesteia:

a) Dacaa antecedentul este adevarat, valoarea de adevar a implicatiei este aceeasi cu a consecventului sau: (1 → q) = q

b) Daca antecedentul este fals, implicatia este adevarata: (0 → q) = 1

c) Daca consecventul este adevarat, implicatia este adevarata: (p → 1) = 1

d) Daca consecventul este fals, valoarea de adevar a implicatiei este aceeasi cu a negatiei antecedentului sau: (p → 0) = ¬p

Echivalenta (simbolizata prin "↔" sau prin "≡") reprezinta o relatie de concordanta logica si este adevarata numai daca ambele propozitii componente au aceeasi valoare de adevar. Vom spune astfel ca doua propozitii sunt logic echivalente daca au aceeasi valoare de adevar. Echivalenta se mai numeste si "dubla implicatie" sau "biconditional", intrucat mai poate fi exprirnata si printr-o conjunctie de implicatii reciproce:

(p↔q) ↔ [(p→q)&(q→p)

Daca unul dintre componentii unei echivalente este adevarat, valoarea de adevar a echivalentei depinde de valoarea celuilalt component: (p ↔ 1) = p

Daca unul dintre componentii unei echivalente este fals, valoarea de adevar a echivalentei este aceeasi cu negatia celuilalt component: (p ↔ 0) = ¬p

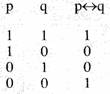
Cei cinci conectori propozitionali fundamentali sunt, prin urmare: