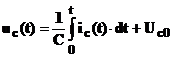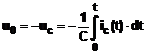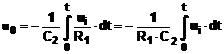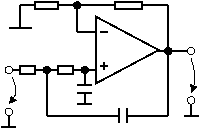Circuite selective in frecventa cu amplificatoare operationale
CIRCUITE SELECTIVE IN FRECVENTA cu
amplificatoare operationale
Scopul lucrarii: familiarizarea studentilor cu circuitele
active selective in frecventa.
2. Circuite de integrare si
derivare si proprietatile lor
Daca
intr-un amplificator inversor R1
sau R2 vor fi inlocuite
prin componente pasive avand intre tensiune si curent o
dependenta de tip integro-diferential, se vor obtine
circuite de integrare sau de derivare. Componenta preferata este
condensatorul, caracterizat prin relatia:
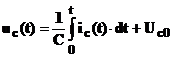 unde C este capacitatea iar UC0 tensiunea
initiala.
unde C este capacitatea iar UC0 tensiunea
initiala.
Curentul condensatorului iC este sta-bilit de
catre circuitul de intrare: 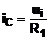
Pentru ca acest curent sa
fie preluat in intregime de circuitul de reactie, tensiunea de
iesire trebuie sa fie egala cu cea de pe condensator,
daca UC0 = 0
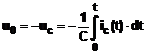

i
C
 R1 C2
R1 C2
 ui iC
ui iC




 u0
u0



 R3
R3


 R2 R4
R2 R4
+Ualim. -Ualim.
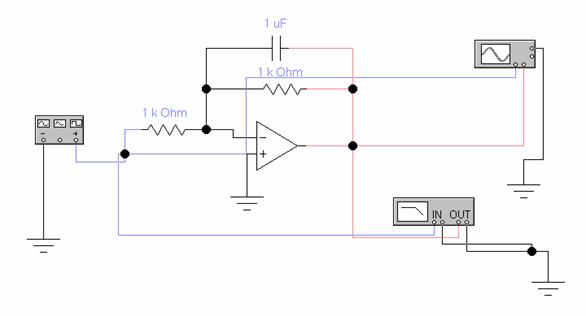
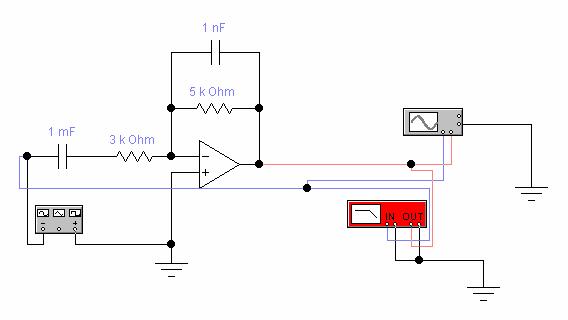
Fig. 2.1 Circuit de integrare
In
final tensiunea de iesire este proportionala cu integrata
tensiunii de intrare:
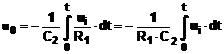
Produsul
R1 C2 se numeste constanta de timp si se
masoara in secunde.
La integratoare o
atentie deosebita trebuie acordata eliminarii tensiunii de
offset care integrata ar produce erori mari. Compensarea offset-ului se
poate face fie prin circuitele de compensare proprii fiecarui AO fie extern ca in figura, prin
potentiometrul R3. Integrarea
poate sa dureze numai pana la saturarea iesirii. De aceea
integrarile se executa pe perioade limitate de timp, dupa care
trebuiesc reiterate prin descarcarea fortata a condensatorului,
cu ajutorul unor comutatoare statice (realizabile de exemplu cu tranzistoare MOS).
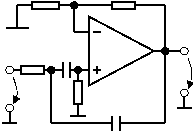
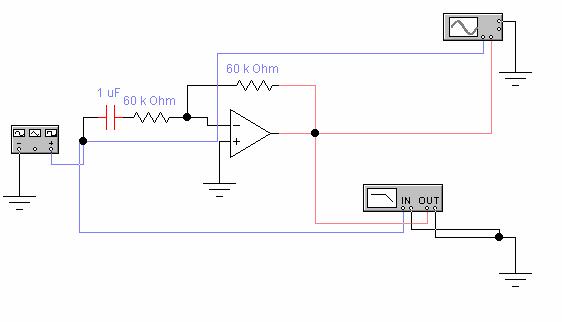
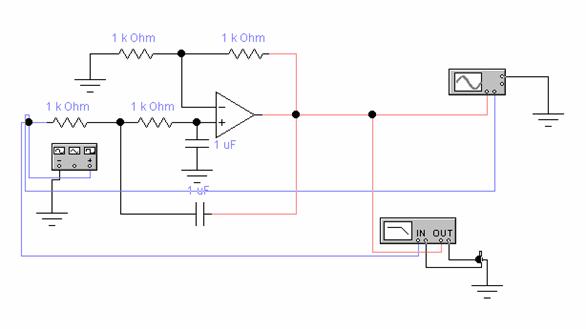
Derivatorul rezulta
inlocuind rezistenta de intrare cu un condensator. Tensiunea
condensato-rului este identica cu tensiunea de intrare, iar curentul
produs in condensator este preluat de circuitul de reactie,
datorita tensiunii de iesire.
iC
=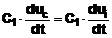
u0
= - R2 iC = 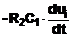
Tensiunea
de iesire este proportionala cu derivata tensiunii de
intrare.
 iC
iC

 C1 R2
C1 R2

 ui iC
ui iC






 u0
u0



Fig. 2.2 Circuit
de derivare
Integrarile
si derivarile sunt operatii extrem de utile in multe
aplicatii, cum ar fi de exemplu masurarile sau reglarile.
Tehnologia analogica prezentata aci poate fi utila prin
simplitate si pretul sau
redus. Aceste circuite au insa si proprietati interesante,
referitoare la caracteristicile lor de frecventa. Sa luam
de exemplu integratorul. Expresia amplificarii sale in tensiune provine
din raportul dintre impedanta condensatorului C2 si
rezistenta de intrare R1 si este:
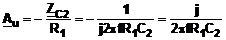
Diagrama
Bode a functiei Au(f) este reprezentata in fig.
2.3, constand dintr-o dreapta care intersecteaza axa 0dB la
frecventa critica 1/(2pR1C2),
la care modulul amplificarii este 1. Defazajul introdus de integrator este
constant negativ: Φ=-p/2. Pentru calculul
inclinarii dreptei vom considera o decada,
adica intervalul dintre doua frecvente aflate in raport de 10.

In
cazul circuitului de derivare singura deosebire consta in inclinarea
pozitiva a caracteristicii, deoarece Au = j2pR1C2.
In acest caz defazajul este pozitiv: Φ=+p
A [dB]



 20
20
 10
10



 0 f
0 f
0,1/2pRC 1/2pRC 10/2pRC
 -10
-10
 -20
-20
derivare integrare
+20dB/dec. -20dB/dec.
 Φ [rad.] derivare
Φ [rad.] derivare




 p
p
p

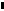
 0 f
0 f
-p 0,1/2pRC 1/2pRC 10/2pRC


 -p
-p
integrare
Figura 2.3 Diagramele
Bode ale circuitelor de integrare si derivare
3. Filtre active
Filtrele
permit controlul caracteristicilor de frecventa ale circuitelor
electronice prin atenuarea sau amplificarea selectiva a unor
portiuni din spectrul de frecvente. Filtrele pot fi pasive sau active
(cu amplificare).
In functie de
modalitatea de realizare a retelelor pasive selective in
frecventa care intra in componenta lor, filtrele se pot
grupa in: filtre RLC si RC. Desi filtrele RLC pot fi realizate
si in varianta pasiva, sunt stabile si pot realiza
caracteristici in frecventa extrem de abrupte, de obicei se
prefera filtrele active RC. Pe langa eliminarea bobinelor (componente
scumpe, ingloband multa manopera si incomode din cauza
cuplajelor magnetice), aceste filtre sunt usor de acordat si pot fi
integrate (mai ales in tehnologie hibrida). Majoritatea filtrelor active
sunt bazate pe AO. In continuare
sunt prezentate principial cele trei tipuri fundamentale de filtre active cu AO.
a) Filtrul trece jos FTJ
Circuitul din figura urmatoare
are doua domenii de functionare distincte:
- la frecvente mici impedanta
capacitatii C2
este mult mai mare decat R2,
neintervenind in circuit, care se comporta ca un amplificator inversor
obisnuit;
- la frecvente mari
impedanta capacitatii C2
sunteaza rezistenta R2
scazand progresiv amplificarea. Frecventa critica de la care
incepe atenuarea este cea la care impedanta capacitatii 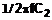 devine egala cu R2. In acest domeniu
circuitul devine practic un integrator.
devine egala cu R2. In acest domeniu
circuitul devine practic un integrator.





 C2 G [dB] -20dB/dec.
C2 G [dB] -20dB/dec.



 60
60


 R1 R2 40
R1 R2 40








 20lg(R2/R1)
20lg(R2/R1)
 ui
20
ui
20


 f [Hz]
f [Hz]





 u0
u0
 0
0


2πR2C2
Dupa
cum se constata din figura, frecventele joase sunt nealterate in
timp ce frecventele mari sunt rejectate. Panta caracteristicii la
frecvente mari este de -20dB/dec.
Se accepta aproximarea caracteristicii de frecventa prin
segmente de dreapta, care poate produce o eroare maxima de 3dB in zona frecventei critice.
Caracteristica reala este reprezentata cu linie intrerupta.