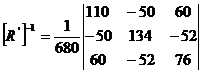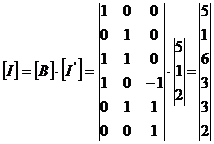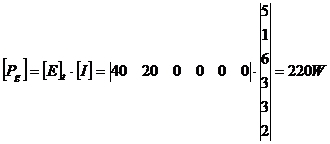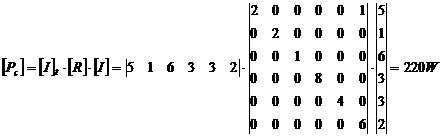Metoda curentilor de
ochiuri (ciclici)
Metoda curentilor
de ochiuri, numita si metoda curentilor ciclici (Maxwell) prezinta avantajul ca
opereaza cu un numar mai mic de variabile fata de metoda
teoremelor lui Kirchhoff si
anume, cu O < L, unde O este numarul de ochiuri
fundamentale ale retelei.
Marimile variabile in
ecuatiile retelei vor fi in acest caz curentii de ochiuri
(ciclici) 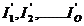 - curenti fictivi
atribuiti ochiurilor fundamentale, astfel incat curentul din fiecare
latura k sa fie egal cu
suma algebrica a curentilor ciclici care parcurg latura
respectiva:
- curenti fictivi
atribuiti ochiurilor fundamentale, astfel incat curentul din fiecare
latura k sa fie egal cu
suma algebrica a curentilor ciclici care parcurg latura
respectiva:
|
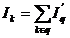 , q = 1,2,.,O , q = 1,2,.,O
|
|
Sumarea se efectueaza pentru
toti curentii ochiurilor q carora
le apartine latura k.
Matematic,
relatia (4.4.39) reprezinta o schimbare liniara de
variabila de la L necunoscute
(curentii laturilor) la O
necunoscute (curentii fictivi atribuiti ochiurilor fundamentale).
Acest lucru este posibil numai in conditiile asigurarii
compatibilitatii cu sistemul ecuatiilor lui Kirchhoff. Astfel, cele (N-1)
ecuatii date de prima teorema a lui Kirchhoff sunt identic satisfacute, deoarece fiecare curent
ciclic intra si iese odata in fiecare nod, aducand o
contributie nula la curentul total prin suprafata inchisa
care cuprinde nodul:
|
 , q = 1,2,.O , q = 1,2,.O
|
|
Restul de O variabile vor fi univoc determinate de
cele L - (N-1) = O ecuatii ramase, date de cea de-a doua teorema a
lui Kirchhoff:
|
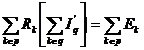 , , 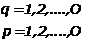
|
|
unde:
|
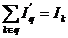 , conform
relatiei (4.4.39) , conform
relatiei (4.4.39)
|
|
Ordonand
relatia (4.4.41) dupa curenti, se mai poate scrie:
|
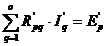 , q = 1,2,.,O , q = 1,2,.,O
|
|
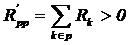
unde:
este rezistenta proprie a ochiului p, respectiv suma aritmetica a
rezistentelor laturilor care alcatuiesc ochiul p;
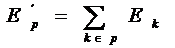 este rezistenta de cuplaj dintre
ochiurile p si q, pozitiva daca
este rezistenta de cuplaj dintre
ochiurile p si q, pozitiva daca 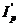 si
si 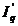 au acelasi sens
prin laturile comune si negativa daca au sensuri contrare; in
cazul in care ochiurile p si q nu au laturi comune, rezulta
ca
au acelasi sens
prin laturile comune si negativa daca au sensuri contrare; in
cazul in care ochiurile p si q nu au laturi comune, rezulta
ca 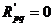 ;
;
este t.e.m. fictiva de ochi, egala cu suma
algebrica a t.e.m. din laturile care alcatuiesc ochiul de circuit p; t.e.m. se iau cu (+) daca
sensurile lor coincid cu sensul de parcurs pe ochi ( sens de
referinta), respectiv - cu sensurile curentilor de ochiuri,
si cu (-) in caz contrar.
Dezvoltat, sistemul de ecuatii se scrie sub
forma:
Prin rezolvarea sistemului (4.4.43) se obtin
curentii de ochiuri (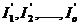 ). Utilizand transformarea liniara (4.4.39) se
calculeaza apoi curentii de laturi (
). Utilizand transformarea liniara (4.4.39) se
calculeaza apoi curentii de laturi (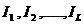 ).
).
Etapele care trebuie
parcurse la rezolvarea unei retele de c.c. prin aplicarea acestei metode
sunt:
Determinarea ochiurilor fundamentale si
alegerea arbitrara a sensurilor curentilor ciclici ale acestora, care
reprezinta, de regula, si sensurile de referinta pe
ochiuri.
Calculul rezistentelor proprii si de
cuplaj ale ochiurilor, respectiv al t.e.m. de ochiuri.
Scrierea sistemului de ecuatii ale
curentilor ciclici si determinarea acestora.
Alegerea arbitrara a sensurilor
curentilor din laturi, daca acestea nu au fost date de la inceput.
Calculul curentilor din laturi cu
relatia (4.4.39), sumarea fiind facuta pentru toti
curentii ochiurilor q, carora le apartine latura k.
Verificarea rezultatelor obtinute (de
exemplu cu teorema de bilant a puterilor).
Forma
matriceala a metodei
Aceasta
forma se utilizeaza pentru retele de dimensiuni mari.
Sub forma
matriceala, sistemul de ecuatii (4.4.43) se poate scrie:
unde:
Matricea 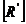 este de forma:
este de forma:
Matricea 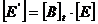 are forma:
are forma:
|
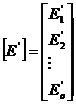 , fiind o matrice
vector-coloana. , fiind o matrice
vector-coloana.
|
|
Prin
rezolvarea sistemului (4.4.44) se obtine:
unde 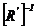 este inversa matricii
este inversa matricii 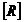 .
.
Matricea
curentilor ciclici este un vector coloana de forma:
Curentii
reali din laturile retelei se determina cu relatia:
Aplicarea metodei sub forma matriceala se
face dupa urmatorul algoritm:
Se aleg sensurile curentilor ciclici din
ochiurile fundamentale ale relatiei (de obicei aceleasi cu sensurile
de parcurs pe ochiuri).
Se formeaza matricele 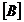 - de
apartenenta a laturilor la ochiuri ( matricea de conexiune a
retelei) si
- de
apartenenta a laturilor la ochiuri ( matricea de conexiune a
retelei) si 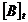 - transpusa acesteia.
- transpusa acesteia.
Se formeaza matricele 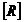 si
si 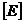 .
.
Se calculeaza matricele 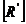 si
si 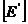 , cu relatiile (4.4.46) si (4.4.47).
, cu relatiile (4.4.46) si (4.4.47).
Se calculeaza matricea inversa 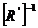 .
.
Se calculeaza matricea 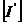 .
.
Se calculeaza matricea 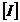 .
.
Se verifica rezultatele. In acest scop se
poate utiliza, de pilda, teorema bilantului puterilor sub forma
matriceala:
respectiv:
Aplicatie
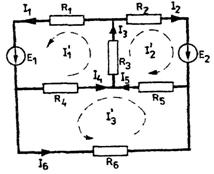
Se da circuitul
din fig. 4.4.18 pentru care se cunosc 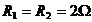 ;
; 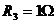 ;
; 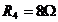 ;
; 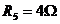 ;
; 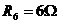 ;
; 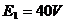 ;
;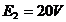 . Sa se determine curentii din laturi folosind
metoda curentilor ciclici, sub forma matriceala.
. Sa se determine curentii din laturi folosind
metoda curentilor ciclici, sub forma matriceala.
|
|
|
Fig. 4.4.18 Aplicatie
|
Rezolvare:
Se aleg sensurile indicate
pe figura pentru curentii ciclici  .
.
Se
formeaza matricea de conexiune si transpusa acesteia:
|
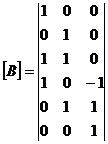 ; ; 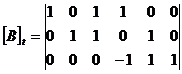
|
|
Se
formeaza matricele  si
si  si se
calculeaza matricele
si se
calculeaza matricele 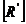 si
si 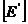 .
.
Ca urmare,
curentii ciclici pot fi calculati cu matricea:
Curentii
din laturi sunt:
Verificare
Se vede
ca se verifica relatia de
bilant:


 , q = 1,2,.O
, q = 1,2,.O 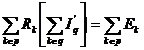 ,
, 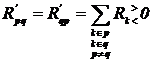
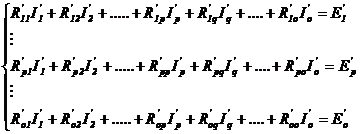
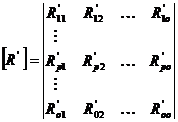
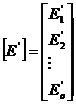 , fiind o matrice
vector-coloana.
, fiind o matrice
vector-coloana. 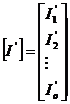

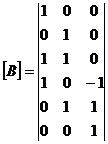 ;
; 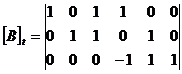

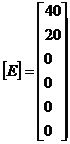
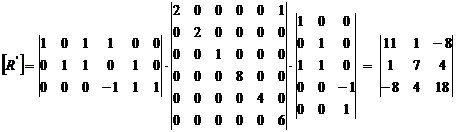
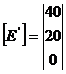 ;
;