Obtinerea
functiei criteriu in limbaj intrare-iesire
Importanta criteriilor integrale pentru
optimizarea dinamica a sistemelor automate a fost prezentata in capitolul 1. In
urmatoarele capitole sunt ilustrate obtinerea functiei criteriu si determinarea
solutiei optime in cazul descrierii comportarii sistemelor automate in limbaj
intrare-iesire (capitolele 2 si 3) si determinarea solutiilor optime in cazul
folosirii limbajului intrare-stare-iesire(capitolele 4, 5 si 6).
1. Principalele tipuri de criterii integrale
Limbajul intrare-iesire se utilizeaza in
cazul schemelor clasice de treglare automata in functie de marimile de iesire,
de tipul schemei din figura 1.13, cu blocul de reglare RA instalat pe calea
directa (spre deosebire de schemele moderne de reglare in functie de stare,
unde blocul de reglare este instalat pe reactiile in functie de stare, unde
blocul de reglare este instalat pe reactiile in functie de stare, ca in
subcapitolul 5.3).
Dupa cum s-a specificat in paragraful 1.2,
criteriile integrale pot asigura optimizarea regimurilor dinamice provocate
atat de variatii ale marimii de referinta, cat si de variatii ale
perturbatiilor.
Cele mai utilizate criterii integrale sunt
cele patratice, de forma (1.5)
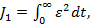 (1)
(1)
functia criteriu (1)
reprezentand integral patratului erorii(in limba engleza "integral of error
squared" ISE).
Eliminarea influientei nedorite a
semnului erorii ε asupra
valorii functiei criteriu poate fi obtinuta si prin utilizarea unei integrale
de forma
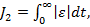 (2)
(2)
functia criteriu (2)
reprezentand integral valorii absolute a erorii (in limba engleza "integral of
absolute error" IAE).
Daca in (2) se introduce o ponderare cu
valoriile timpului t, se obtine functia criteriu
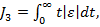 (3)
(3)
reprezentand
integral produsului dintre timp si valoarea absoluta a erorii (in limba engleza
"integral of time multiplied by absolute error" ITAE).
Minimizarea functiei criteriu 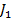 - din (1) -
asigura un regim tranzitoriu de calitate buna pentru limitarea valorilor erorii
ε. Calitatea regimului
tranzitoriu devine mai buna daca o data cu limitarea valorilor erorii ε se asigura si o limitarea a valorilor
derivatei
- din (1) -
asigura un regim tranzitoriu de calitate buna pentru limitarea valorilor erorii
ε. Calitatea regimului
tranzitoriu devine mai buna daca o data cu limitarea valorilor erorii ε se asigura si o limitarea a valorilor
derivatei 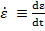 , deoarece
in acest caz variatia erorii nu poate avea pante mari si ca urmare se evita
suprareglaje
, deoarece
in acest caz variatia erorii nu poate avea pante mari si ca urmare se evita
suprareglaje 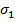 ridicate
(vezi figura 1.14). Limitarile mentionate pot fi asigurate de un criteriu
patratic de forma
ridicate
(vezi figura 1.14). Limitarile mentionate pot fi asigurate de un criteriu
patratic de forma
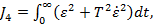 (4)
(4)
unde T este o
constanta de timp care pondereaza contributia celui de-al doilea termen.
Prin considerarea derivatelor de ordin superior se obtine un criteriu de
forma
 (5)
(5)
unde 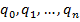 sunt
factori de ponderare.
sunt
factori de ponderare.
Daca pe langa o calitate buna a
regimului tranzitoriu se urmareste si reducerea consumului de energie pentru
reglare, atunci functia criteriu capata aspectul (1.66), respective
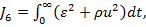 (6)
(6)
Unde ρ este un factor de ponderare;
u - marimea de comanda.
Trecand la limbajul
intrare-stare-iesire, combinarea unor criteria de forma (5) si (6) conduce la
functia criteriu
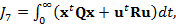 (7)
(7)
unde x este vectorul de stare;
u - vectorul marimilor de comanda (in cazul
general al unei intalatii tehnologice multivariabile);
Q,R
- matrice de ponderare.
Daca se impune si un anumit timp final 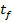 pentru
incheierea regimului tranzitoriu si intrarea in noul regim stationar, atunci
prin adougarea unui termen suplimentar in (7) se obtine o functie criteriu de
tipul (1.72):
pentru
incheierea regimului tranzitoriu si intrarea in noul regim stationar, atunci
prin adougarea unui termen suplimentar in (7) se obtine o functie criteriu de
tipul (1.72):
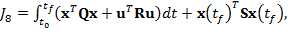 (8)
(8)
unde 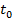 este
momentul initial, cand se aplica comanda u;
este
momentul initial, cand se aplica comanda u;
S - matrice de
ponderare.
Dupa cum s-a mentionat in paragraful 1.2,
termenul integral din criteriul  asigura o
buna calitate a regimului tranzitoriu, iar al doilea termen asigura o
comportare buna la intrarea in noul regim stationar, in momentul
asigura o
buna calitate a regimului tranzitoriu, iar al doilea termen asigura o
comportare buna la intrarea in noul regim stationar, in momentul 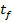 , deci cand
este importanta obtinerea egalitatii
, deci cand
este importanta obtinerea egalitatii
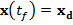 ,
,
sau in cazul cand
pentru o anumita variatie a marimii de
referinta se urmareste ca vectorul marimilor de iesire 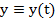 (in cazul
general, al sistemelor multivariabile) sa aiba o anumita variatie dorita
(in cazul
general, al sistemelor multivariabile) sa aiba o anumita variatie dorita 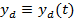 , atunci functia criteriu poate fi exprimata sub
forma
, atunci functia criteriu poate fi exprimata sub
forma
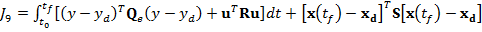 (9)
(9)
unde 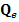 , R si S sunt matrice de ponderare.
, R si S sunt matrice de ponderare.
Termenul integral - prezentand anumite
analogii cu (1.70) - asigura calitatea regimului tranzitoriul; termenul al
doilea asigura comportarea dorita la intrarea in noul regim stationar, in
momentul 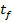 .
.
Folosirea criteriilor 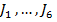 , formulate in limbajul clasic intrare-iesire,
presupune cunoscuta structura blocului de reglare (de regula un bloc de reglare
tipizat) amplasat pe calea directa, ca in figura (1.13), iar prin minimizarea
criteriului amplasat pe calea directa se obtin valorile optime ale parametrilor
regulatorului. Utilizarea acestor criteria are avantajul ca necesita numai
eroarea ε derivatele ale
acesteia si marimea de comanda u, deci numai marimi usor masurabile.
, formulate in limbajul clasic intrare-iesire,
presupune cunoscuta structura blocului de reglare (de regula un bloc de reglare
tipizat) amplasat pe calea directa, ca in figura (1.13), iar prin minimizarea
criteriului amplasat pe calea directa se obtin valorile optime ale parametrilor
regulatorului. Utilizarea acestor criteria are avantajul ca necesita numai
eroarea ε derivatele ale
acesteia si marimea de comanda u, deci numai marimi usor masurabile.
Folosirea criteriilor 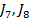 , sunt formulate in limbajul modern
intrare-stare-iesire, nu presupune adoptarea unei structure tipizate pentru
blocul de reglare, dar necesita cunoasterea tuturor componentelor vectorului de
stare x; intrucat acestea nu pot fi totdeauna masurate, poate devein necesara
introducerea unor estimatoare de stare [1,3].
, sunt formulate in limbajul modern
intrare-stare-iesire, nu presupune adoptarea unei structure tipizate pentru
blocul de reglare, dar necesita cunoasterea tuturor componentelor vectorului de
stare x; intrucat acestea nu pot fi totdeauna masurate, poate devein necesara
introducerea unor estimatoare de stare [1,3].
Criteriul 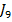 este
formulat atat in functie de iesirile y, cat si de starea x.
este
formulat atat in functie de iesirile y, cat si de starea x.
Aspectul criteriilor integrale in limbaj
intrare-stare-iesire pentru cazul sistemelor discrete este prezentat in
subcapitolul 5.5 si in capitolul 9.
Obtinerea
functiei criteriu 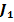 prin relatii directe
prin relatii directe
Expresiile unor functii criteriu pot fi
obtinute direct, pornind de la functia de transfer a sistemului si de la
transformata Laplace a marimii de referinta sau a perturbarii. Posibilitatea
unor relatii directe de acest tip poate fi ilustrata pentru criteriul 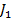 din (1)
avand loc relatia [1]:
din (1)
avand loc relatia [1]:
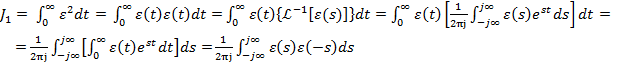 (10)
(10)
Presupunand ca aparitia regimului
tranzitoriu a fost determinate de o variatie a marimii de referinta 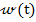 , au loc relatiile [1]
, au loc relatiile [1]
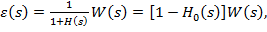 (11)
(11)
unde H(s) si 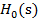 sunt
functiile de transfer ale sistemului (cu
bucla deschisa si cu bucla inchisa, in ipoteza reactiei principale directe) in
raport cu marimea de referinta.
sunt
functiile de transfer ale sistemului (cu
bucla deschisa si cu bucla inchisa, in ipoteza reactiei principale directe) in
raport cu marimea de referinta.
Intrucat structura blocului de reglare
este presupusa cunoscuta, functiile de transfer H(s) si 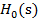 pot fi
determinate usor si contin parametrii regulatorului automat sub forma unor
variabile.
pot fi
determinate usor si contin parametrii regulatorului automat sub forma unor
variabile.
Inlocuind (11) in (10) se obtine
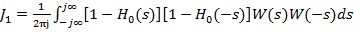 (12)
(12)
In ceea ce se priveste marimea de
referinta 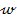 , se presupune ca aceasta are o variatie treapta
unitara, respectiv
, se presupune ca aceasta are o variatie treapta
unitara, respectiv
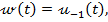 (13)
(13)
deci
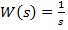 (14)
(14)
Considerarea unei variatii treapta a
marimii de referinta se bazeaza pe constatarea ca daca optimizarea parametrilor
regulatorului asigura o comportare buna a sistemului in regimurile tranzitorii
provocate de acest tip de semnale, atunci este asigurata o comportare buna si
in regimurile tranzitorii provocate de alte tipuri de variatii ale marimilor de
referinta.
Daca in locul bunei calitati a
regimurilor tranzitorii provocate de modificarea valorilor marimilor de
referinta se urmareste o calitate buna a regimurilor tranzitorii provocate de
perturbari, atunci se considera 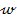 = 0 si
= 0 si 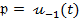 si se
calculeaza functia de transfer
si se
calculeaza functia de transfer 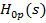 in raport
cu perturbarea [1], rezultand pentru transformata Laplace Y(s) a marimii de
iesire y expresia
in raport
cu perturbarea [1], rezultand pentru transformata Laplace Y(s) a marimii de
iesire y expresia
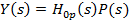 (15)
(15)
Pe
de alta parte
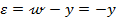 (16)
(16)
intrucat s-a
considerat 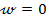 - deci din (15) si (16)
rezulta
- deci din (15) si (16)
rezulta
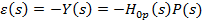 (17)
(17)
Inlocuirea acestei expresii in (10) permite
ca pentru criteriu 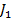 sa se
obtina o relatie corespunzatoare in locul expresiei (12), parametrii
regulatorului intervenind sub forma unei variabile.
sa se
obtina o relatie corespunzatoare in locul expresiei (12), parametrii
regulatorului intervenind sub forma unei variabile.
Din (10) si (12) se constata ca criteriul 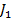 poate fi
exprimat in functie de transformata Ԑ(s) sau in functie de functia de transfer
poate fi
exprimat in functie de transformata Ԑ(s) sau in functie de functia de transfer 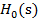 si de
transformata W(s) din (14). Asemenea relatii au fost stabilite [2,1] pornind de
la forma generala a transformatei erorii
si de
transformata W(s) din (14). Asemenea relatii au fost stabilite [2,1] pornind de
la forma generala a transformatei erorii
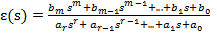 (18)
(18)
Se poate verifica usor ca are loc relatia
r - m = 1, (19)
iar daca functia
de transfer a sistemului deschis H(s) are un pol in origine - necesar pentru a
asigura o eroare stationara nula la semnale de referinta de tipul(13) [1], ceea
ce permite folosirea criteriului 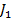 - atunci
are loc conditia
- atunci
are loc conditia
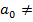 0 (20)
0 (20)
importanta pentru
aplicarea relatiilor directe pentru obtinerea criteriului 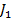
Pentru verificarea relatiei (19), functia de
transfer H(s) din (11), reprezentand raportul a doua polinoame
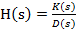 (21)
(21)
este pusa sub
forma
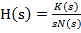 (22)
(22)
fiind evidentiata
prezenta unui pol in origine ; in polinoamele K(s) si N(s) nu apare deci s ca
factor
Intrucat s-a presupus reactia principala
directa, rezulta [1]
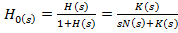 (23)
(23)
iar prin
inlocuirea expresiilor (14) si (23) in (11) se obtine
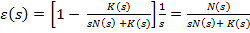 (24)
(24)
Intrucat
polinomul K(s) nu contine variabila s ca factor, din (24) se constata ca la
numitor nu apare s factor comun si deci conditia (20) este asigurata in (18).
Totodata, intrucat in (21) si (22) gradul
numitorului este totdeauna mai mare decat al numaratorului - pentru toate
sistemele automate din practica industriala [1] - rezulta ca numitorul din (24)
are gradul polinomului sN(s) = D(s) ; ca urmare, relatia (24) confirma conditia
(19).
Dupa
cum va rezulta din paragraful 5.1.3 conditia (19) care este valabila pentru
transformata ε(s) a
erorii in cazul prezentei polului in origine in functia de transfer H(s) - nu
mai este valabila in cazul transformatei altor marimi, cum sunt transformatele 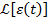 sau
U(s).
sau
U(s).
Pentru cazurile in care relatia (19) este
valabila - deci si pentru cazul expresiei ε(s) din (18) - in [2] este stabilita urmatoarea
relatie directa care permite obtinerea expresiei criteriului 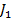 prin
intermediul coeficientilor din (18):
prin
intermediul coeficientilor din (18):
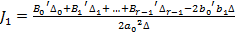 (25)
(25)
unde:
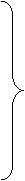
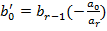
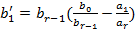
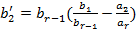
. (26)
.
.
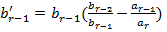
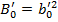
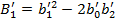
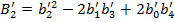
. (27)
.
.
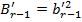
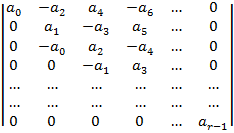 (28)
(28)
iar determinantii
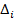 se obtin
din
se obtin
din 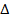 prin
inlocuirea coloanei i+1 prin coloana
prin
inlocuirea coloanei i+1 prin coloana
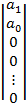 (29)
(29)
3. Obtinerea functiilor criteriu 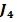 si
si 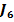 prin relatii directe
prin relatii directe
Criteriul 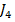 - din (4) -
poate fi pus sub forma
- din (4) -
poate fi pus sub forma
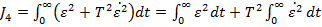 (30)
(30)
si notand
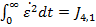 (31)
(31)
se obtine
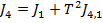 (32)
(32)
avand in vedere
si (1).
Intrucat in paragraful anterior este
prezentata relatia (25) care permite obtinerea expresiei 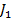 , problema
determinarii expresiei criteriul
, problema
determinarii expresiei criteriul 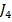 se reduce
la obtinerea expresiei
se reduce
la obtinerea expresiei 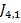 .
.
Comparand (31) cu (1) se constata ca daca
se deterimina transformata 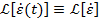 obtinandu-se o expresie analoaga cu (18) -
atunci expresia
obtinandu-se o expresie analoaga cu (18) -
atunci expresia 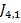 poate
rezulta prin interemdiul unei relatii analoage cu (25).
poate
rezulta prin interemdiul unei relatii analoage cu (25).
Conform relatiilor de transformare,
rezulta
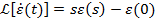 (33)
(33)
si inlocuind (24)
cu (33) se obtine
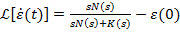 (5.34)
(5.34)
Intrucat s-a considerat variatia treapta
unitara (13) pentru marimea de referinta rezulta
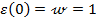 (35)
(35)
Deoarece imediat
dupa variatia marimii de referinta 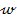 (la
(la 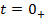 ) marimea de iesire y are inca valoarea
considerate conventional egala cu zero - si din (1.61) rezulta
) marimea de iesire y are inca valoarea
considerate conventional egala cu zero - si din (1.61) rezulta 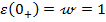
Inlocuind (35) in (5.34) rezulta
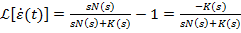 (36)
(36)
Intrucat in marea majoritate a cazurilor
din practica industrial diferenta dintre gradele numitorului si numaratorului
functiei de transfer H(s) - din (21) si (22) - este egala cu 2 sau mai mare,
rezulta ca aceeasi diferenta se pastreaza si pentru expresia (36), deci
conditia (19)
nu mai este
valabila pentru transformata 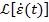 .
.
Ca urmare, pentru transformata 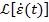 se va
obtine o expresie de forma
se va
obtine o expresie de forma
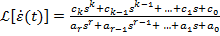 (37)
(37)
cu
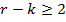 (38)
(38)
Pentru cazurile in care este valabila
conditia (38), in [2] este stabilita urmatoarea relatie pentru obtinerea
expresiei 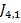 prin
intermediul coeficientilor din (37):
prin
intermediul coeficientilor din (37):
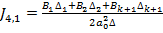 (39)
(39)
unde
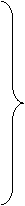
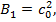
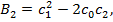
.
.
.
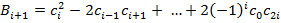 (40)
(40)
.
.
.
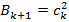
iar determinantii 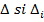 se obtin ca
in paragraful 5.1.
se obtin ca
in paragraful 5.1.
Inlocuind om (32) expresiile 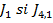 - din (25)
si (39) - se obtine criteriul
- din (25)
si (39) - se obtine criteriul 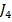 . In
paragraful 5.1. sunt prezentate indicatii pentru alegerea constantei in timp T
din (32), iar in paragraful 5. este ilustrata folosirea relatiilor directe
pentru obtinerea criteriului
. In
paragraful 5.1. sunt prezentate indicatii pentru alegerea constantei in timp T
din (32), iar in paragraful 5. este ilustrata folosirea relatiilor directe
pentru obtinerea criteriului 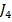 .
.
Pentru obtinerea expresiei aferente
criteriului 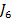 , relatia (6)
se transcribe sub forma
, relatia (6)
se transcribe sub forma
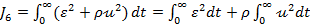 (41)
(41)
si notand
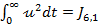 (42)
(42)
rezulta
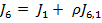 (43)
(43)
problema
reducandu-se deci la obtinerea expresiei 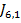 din (42).
din (42).
Daca se determina transformata U(s),
atunci obtinerea expresiei 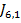 este
imediata, folosind o relatie de tipul (25) sau de tipul (39), dupa cum
polinoamele de la numitorul si numaratorul transformatei U(s) indeplinesc
conditia (19) sau conditia (38).
este
imediata, folosind o relatie de tipul (25) sau de tipul (39), dupa cum
polinoamele de la numitorul si numaratorul transformatei U(s) indeplinesc
conditia (19) sau conditia (38).
Din figura 1.13 se constata ca
transformata U(s) se obtine usor din transformata 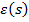 , conform relatiei
, conform relatiei
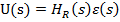 (44)
(44)
unde 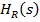 este
functia de transfer a regulatorului (de structura presupusa conoscuta),
parametrii regulatorului - prin minimizarea functiei criteriu obtinandu-se
valorile optime ale acestor parametrii - intervenind ca variabile in expresia
este
functia de transfer a regulatorului (de structura presupusa conoscuta),
parametrii regulatorului - prin minimizarea functiei criteriu obtinandu-se
valorile optime ale acestor parametrii - intervenind ca variabile in expresia 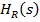
Relatiile (25) si (39) permit astfel
obtinerea directa a criteriilor 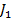
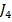 si
si 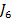 . Pe o cale analoaga cu cea descrisa mai sus cele
doua relatii permit si obtinerea criteriului
. Pe o cale analoaga cu cea descrisa mai sus cele
doua relatii permit si obtinerea criteriului 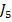 , folosind expresiile transformatelor Laplace
, folosind expresiile transformatelor Laplace 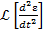
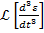 etc.
etc.
4. Obtinerea functiei criteriu prin intermediul
functiilor Liapunov
Daca in (5) coeficientii 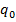
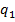
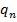 sunt
pozitivi, atunci criteriul
sunt
pozitivi, atunci criteriul 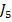 poate fi
pus sub forma
poate fi
pus sub forma
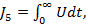 (45)
(45)
unde
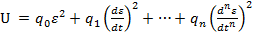 (46)
(46)
este o functie
patratica, pozitiv definita, de variabile 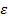
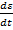 etc.
etc.
Pentru obtinerea expresiei functiilor
criteriu de forma 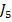 , in [4,5]
se propune alegerea unei functii Liapunov V (patratice, pozitiv definite),
astfel incat sa aiba loc relatia
, in [4,5]
se propune alegerea unei functii Liapunov V (patratice, pozitiv definite),
astfel incat sa aiba loc relatia
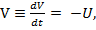 (47)
(47)
functia criteriu
fiind obtinuta prin intermediul acestei functii Liapunov.
Functia U fiind pozitiv definita, rezulta
ca U va fi negativ definit; din (47)
se constata ca functia Liapunov V,
pozitiv definita, va avea derivata in raport cu timpul negativ definita, deci
este asigurata stabilitatea asimptotica a sistemului automat [6, 1].
Obtinerea expresiei functiei criteriu
prin intermediul functiilor Liapunov este ilustrata in continuare pentru
criteriul 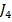 (care
rezulta din
(care
rezulta din 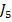 prin
retinerea primilor doi termeni ai integrandului), considerand un sistem de
ordinal II [1], respectiv un sistem automat care in stare inchisa are o functie
de transfer de forma
prin
retinerea primilor doi termeni ai integrandului), considerand un sistem de
ordinal II [1], respectiv un sistem automat care in stare inchisa are o functie
de transfer de forma
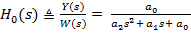 (48)
(48)
Din (23) si (24) se constata ca functia
de transfer 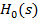 si
transformata
si
transformata 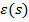 au acelasi
numitor; datorita acestui fapt, in (48) polinomul de la numitor are
coeficientii polinomului de la numitorul din (18)
au acelasi
numitor; datorita acestui fapt, in (48) polinomul de la numitor are
coeficientii polinomului de la numitorul din (18)
Pe
de alta parte, prezenta unui pol in origine in functia de transfer H(s)
determina conditia
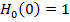 (49)
(49)
- dupa cum rezulta
din (23) si ca urmare in (48) constanta de la numarator are valoarea 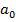 , ceea ce asigura satisfacerea conditiei (49).
, ceea ce asigura satisfacerea conditiei (49).
De cele mai multe ori functiile de
transfer ale sistemelor de ordinal II se exprima in functie numai de doi parametrii,
sub forma [1]
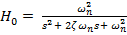 , (50)
, (50)
unde 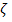 este factorul de amortizare ;
este factorul de amortizare ;
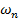 - pulsatia
naturala a sistemului neamortizat.
- pulsatia
naturala a sistemului neamortizat.
Identificand (48)
cu (50) se obtine
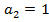 (51)
(51)
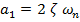 (52)
(52)
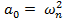 (53)
(53)
Satisfacerea conditiei (49) - care atesta
prezenta unui pol in origine in functia de transfer a sistemului deschis H(s) -
asigura o eroare stationara nula la variatii treapta ale marimii de referinta 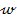 , ceea ce permite aplicarea criteriului
, ceea ce permite aplicarea criteriului 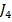 , conform conditiei (1.71). Ca urmare, are loc
relatia
, conform conditiei (1.71). Ca urmare, are loc
relatia
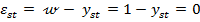 (54)
(54)
- semnul de referinta 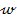 fiind o
treapta unitara - deci
fiind o
treapta unitara - deci
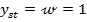 (55)
(55)
Pe de alta parte, marimea de iesire y poate fi pusa sub forma sumei
componentelor stationara (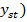 si
tranzistorie (
si
tranzistorie (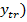 , respectiv
, respectiv
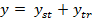 (56)
(56)
Inlocuind in
relatia
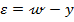 (57)
(57)
expresia (56)
pentru y, se obtine
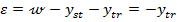 , (58)
, (58)
Din (58) se
obtine
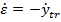
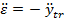 etc (59)
etc (59)
si deci
criteriul 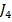 din (4)
poate fi pus sub forma
din (4)
poate fi pus sub forma
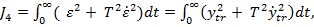 (60)
(60)
avand in vedere (58)
si (59).
Expresia obtinuta in (60)
- pentru sisteme cu o singura marime de
referinta si o singura marime de iesire prezinta anumite analogii cu prima parte
a termenului integral din relatia (9), corespunzatoare unor sisteme
multivariabile, intrucat componentele vectorului 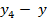 pot fi
considerate marimile
pot fi
considerate marimile 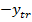 si
si 
Pentru obtinerea functiilor U si V,
care intervin in (47), este indicat ca marimile 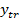 si
si  sa fie
considerate variabile de stare, notand
sa fie
considerate variabile de stare, notand
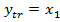 (61)
(61)
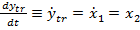 (62)
(62)
Egaland cu zero
numitorul din (48) se obtine ecuatia caracteristica
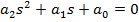 (63)
(63)
si deci regimul
tranzitoriu determinat - de variatia treapta unitara a marimii de referinta 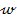 va fi
descris de ecuatia diferentiala [1]
va fi
descris de ecuatia diferentiala [1]
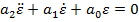
respectiv de ecuatia
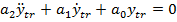 , (64)
, (64)
avand in vedere (58) si (59)
Din (64) se
obtine
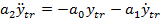
respectiv
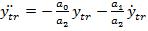 (65)
(65)
Din (62) rezulta
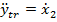 (66)
(66)
si inlocuind (61),
(62) si (66) in (65) se obtine ecuatia de stare
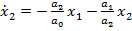 , (67)
, (67)
cealalta ecuatie
de stare fiind reprezentata de ultima parte a egalitatii (62).
Inlocuind (61) si (62) in (60) se obtine
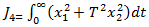 (68)
(68)
si identificand (68)
cu expresia
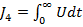 (69)
(69)
- corespunzatoare
relatiei (45) pentru 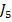 , prin retinerea primilor doi termeni din (46)
obtinandu-se
, prin retinerea primilor doi termeni din (46)
obtinandu-se 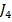 - rezulta
- rezulta
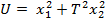 (70)
(70)
Pe de alta parte, din (47) se obtine
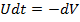 (71)
(71)
si deci din (69)
si (71) rezulta
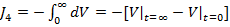 (72)
(72)
Relatia (72) atesta faptul ca criteriul 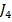 (si in
cazul general criteriul
(si in
cazul general criteriul 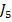 ) poate fi exprimat prin intermediul functiilor
Liapunov.
) poate fi exprimat prin intermediul functiilor
Liapunov.
La 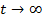 , in noul
regim stationar, devin nule
, in noul
regim stationar, devin nule 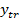 si
si  , deci se anuleaza ambele variabile de stare
, deci se anuleaza ambele variabile de stare 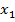 si
si 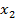 rezultand
rezultand
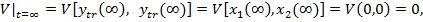 (73)
(73)
intrucat functia V este pozitiv definita si se anuleaza numai cand toate
variabilele de stare sunt nule.
Inlocuind (73) in (72) se obtine
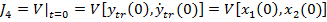 (74)
(74)
Pentru determinarea expresiei 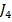 este
necesara alegerea prealabila a functiei V, astfel incat sa fie asigurata
conditia (47), respectiv - avand in vedere (70) astfel incat sa se verifice
relatia
este
necesara alegerea prealabila a functiei V, astfel incat sa fie asigurata
conditia (47), respectiv - avand in vedere (70) astfel incat sa se verifice
relatia
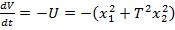 (75)
(75)
Functia V este cautata sub forma [5]
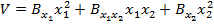 (76)
(76)
coeficientii 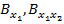 si
si 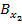 ,fiind determinanti din conditia satisfacerii
relatiei (75).
,fiind determinanti din conditia satisfacerii
relatiei (75).
Derivand (76) in raport cu timpul se
obtine
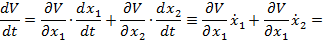
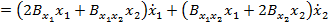 (77)
(77)
Inlocuind in (77) expresiile  si
si 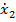 din (62) si
(67), se obtine
din (62) si
(67), se obtine
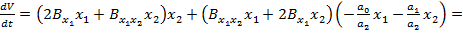
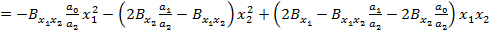 (78)
(78)
Identificand coeficientii din (75) si (78) se obtin
relatiile
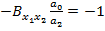 (79)
(79)
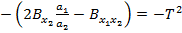 (80)
(80)
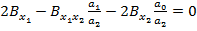 (81)
(81)
rezolvarea acestor ecuatii permitand determinarea
coeficientilor functiei V din (76):
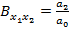 (82)
(82)
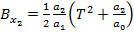 (83)
(83)
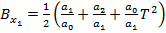 (84)
(84)
Inlocuind (82), (83) si (84) in (76) se obtine
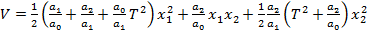 (85)
(85)
Iar din (74) si (85)
rezulta
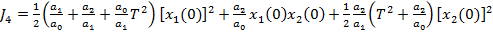 (86)
(86)
Pentru obtinerea expresiei 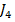 trebuie
determinate valorile marimilor
trebuie
determinate valorile marimilor
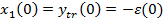 (87)
(87)
si
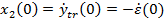 (88)
(88)
avand in vedere (58)
si (59).
Intrucat s-a presupus ca semnalul de
referinta este o treapta unitara, are loc relatia (35) si prin inlocuire in (87)
se obtine
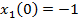 (89)
(89)
Pe de alta parte, la sistemele de ordinal
II - cu functiile de transfer (48) si (50) - raspunsul y la un semnal treapta 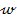 este
tangent la axa timpului in momentul
este
tangent la axa timpului in momentul 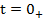 [1] deci
rezulta
[1] deci
rezulta
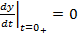 (90)
(90)
din (55), (5,56)
si (90) se obtine astfel
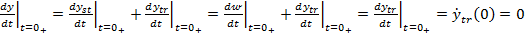 (91)
(91)
si inlocuind (91)
in (88) rezulta
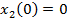 (92)
(92)
Introducand in (86)
valorile 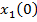 si
si 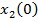 din (89) si
(92), se obtine expresia functiei criteriu
din (89) si
(92), se obtine expresia functiei criteriu
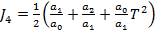 (93)
(93)
Dupa cum se constata din prezentul
paragraf, considerarea anumitor marimi ca variabile de stare este utila si in cazul
caracterizarii sistemului prin functii de transfer - deci in limbaj intrare-iesire - intrucat simplifica
transcrierea unor relatii intermediare.


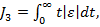 (3)
(3)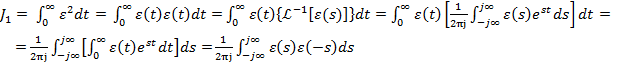 (10)
(10)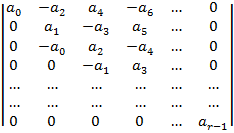 (28)
(28)