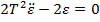Procesul tranzitoriu etalon

Procesul tranzitoriu etalon

Fiecarei functii criteriu ii corespunde un anomit proces tranzitoriu "etalon", respectiv prin adoptarea valorilor optime ale parametrilor regulatorului - care asigura minimizarea functiei criteriu - se obtine procesul tranzitoriu cel mai apropiat posibil de cel etalon.

Pentru ilustrarea aspectului unui proces tranzitoriu etalon se considera criteriul 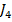din (2.4), care poate fi pus sub forma:

(3.0)

Intrucat se presupune ca procesul tranzitoriu este determinat de o variatie treapta a marimii de referinta 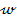, folosirea criteriului 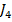implica o valoare nula a erorii stationare, deci

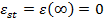(3.1)

si ca urmare

(3.2)

Intrucat (3.2) in (3.0) se obtine

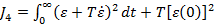(3.3)

Procesul tranzitoriu etalon va fi cel care asigura pentru criteriul 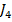valoarea minima posibila , aceasta rezultand cand primul termen din (3.3) se anuleaza, respectiv cand are loc relatia

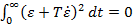(3.4)

care este posibila numai daca este indeplinita conditia

(3.5)

Ecuatia diferentiala (3.5) are ca solutie exponentiala

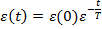(3.6)

care reprezinta procesul tranzitoriu etalon aferent criteriului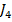

Inlocuind (3.5) in (3.3) se obtine

(3.7)

si se considera ca valoarea minima posibila a functiei criteriu depinde de valoarea initiala - deci de valoarea variatiei treapta a semnalului de referinta 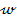, conform cu (2.35) - si de constanta de timp T, care pondereaza contributia celui de-al doilea termen din (2.4).

Ca urmare, adoptarea valorii constantei T se face in concordanta cu aspectul dorit pentru procesul tranzitoriu etalon , deci in concordanta cu aspecutl urmarit pentru procesul tranzitoriu, real care se va apropia de cel etalon.

Expresia procesului tranzitoriu etalon (3.6) poate fi obtinuta si prin intermediul calculului variational. Astfel, scriind functia cirteriu 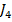sub forma

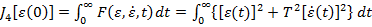(3.8)

extremala 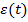- care asigura un extrem al functiei criteriu - trebuie sa satisfaca ecuatia Euler-Lagrange

(3.9)

Din (3.8) se obtine

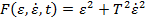(3.10)

si deci rezulta

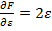(3.11)

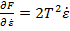(3.12)

si inlocuind (3.11) si (3.12) in (3.9) se obtine ecuatia diferentiala

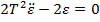
respectiv

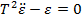(3.13)

cu solutia

(3.14)

avand in vedere (3.1) .

Ecuatia caracteristica aferenta ecuatiei diferentiale (3.13) are aspectul

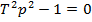
cu radacinile

(3.15)

si deci rezulta solutia ecuatia diferentiale sub forma

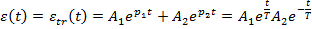(3.16)

Pentru a fi satisfacuta relatia (3.1) este necesara conditia

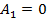(3.17)

(3.18)

Inlocuind (3.17) si (3.18) in (3.16) rezulta

deci se regaseste procesul tranzitoriu etalon (3.6) .

Din (2.1) si (2.4) se constata ca functia criteriu rezulta din 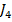pentru

(3.19)

si in acest caz procesul tranzitoriu etalon (3.6) tinde catre o treapta, dar variatia abrupta a marimii de iesire 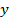(si a erorii ε) in portiunea initiala a regimului tranzitoriu determina depasirea valorii stationare 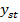si aparitia unui suprareglaj (ca in figura 1.14), deci in locul unui proces tranzitoriu aperiodic se obtine un proces tranzitoriu oscilant.

In [5] se arata ca adoptarea criteriului 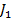conduce la un proces tranzitoriu care poate fi aproximat prin expresia

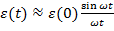(3.20)

cu un suprareglaj de circa 20% si o amortizare relativ lenta a oscilatiilor de pulsatie ω