Studiul golirii unui rezervor cu lichid
 DEFINITII SI FORMULE
DEFINITII SI FORMULE
Metoda Rayleigh
T
procedura utilizata pentru a gasi
formule matematice compatibile cu o lege a fizicii care depinde de un set dat
de marimi fizice
Ecuatia de
continuitate
T
exprima conservarea masei de
substanta
T
in cazul curgerii unui lichid, forma ei este urmatoarea
: S1v1 = S2v2, unde S1 si S2
sunt ariile sectiunilor transversale ale jetului de lichid, iar v1 si v2 sunt vitezele de curgere a
lichidului in punctele corespunzatoare celor doua sectiuni
T
produsul Sv
este egal cu debitul volumic al lichidului D
Debit
T
debitul poate fi de doua tipuri : masic sau
volumic
T
debitul masic Dm
reprezinta masa de lichid care trece in unitatea de timp prin
sectiunea transversala a unui jet de lichid
T
debitul volumic D
reprezinta volumul de lichid care trece in unitatea de timp prin
sectiunea transversala a unui jet de lichid
T
notand densitatea lichidului cu r, relatia intre debitul
masic si debitul volumic este : Dm
= rD
Conservarea energiei
mecanice
T
este o lege generala a fizicii care se
aplica sistemelor fizice izolate de exterior, in interiorul carora nu
actioneaza forte neconservative (de exemplu, forte de frecare)
T
aplicand legea conservarii energiei
mecanice in cazul curgerii laminare (fara vartejuri) a unui lichid se
obtine legea lui Bernoulli :
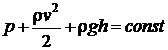
unde p este presiunea statica, r este
densitatea lichidului, v este viteza
de curgere a lichidului, h este
inaltimea masurata in raport cu un nivel de
referinta, iar g este acceleratia
gravitationala. Termenul 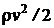 se numeste presiune dinamica, iar termenul rgh se numeste presiune de pozitie
se numeste presiune dinamica, iar termenul rgh se numeste presiune de pozitie

ASPECTE TEORETICE
GOLIREA
REZERVORULUI
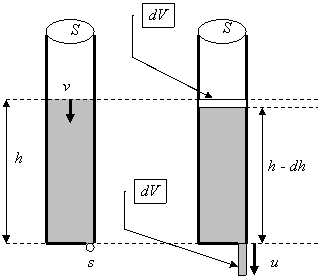
Consideram
un rezervor cilindric care contine o cantitate de lichid. Aria
transversala a rezervorului este S.
Lichidul se poate scurge printr-un orificiu de sectiune s, aflat la baza rezervorului.
Initial, inaltimea lichidului din rezervor este h0. Dupa un timp t de la inceputul scurgerii,
inaltimea lichidului din rezervor devine h.
Dorim
sa determinam legea care stabileste modul in care
inaltimea h variaza in
functie de timpul t. In lipsa
oricaror alte informatii, putem recurge la metoda Rayleigh. In acest
scop, va trebui mai intai sa stabilim lista marimilor fizice
implicate in procesul de curgere a lichidului. Evident, marimi implicate
sunt : h, h0, t, S si s. La acestea trebuie adaugata acceleratia gravitationala
g deoarece curgerea se face sub
influenta gravitatiei si, eventual, densitatea lichidului r. Vom
mai face ipoteza ca procesul de scurgere se desfasoara in
conditii ideale : frecarile sunt neglijabile, curgerea este laminara,
etc. Legea pe care o cautam va fi de forma :
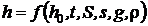
Conform conditiei de omogenitate dimensionala,
rezulta :
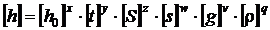
Inlocuind cu formulele dimensionale, rezulta :
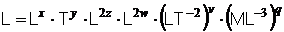
sau :
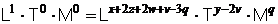
Rezulta sistemul de ecuatii
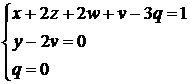
Solutiile sale sunt :
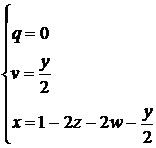
Conform ipotezei lui Rayleigh, rezulta :
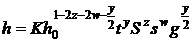
sau :
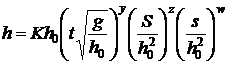
Pe langa factorul adimensional K exista trei parametri (y,
z, w) cu valori nedeterminate. Consecinta este aceea ca
exista un numar infinit de
combinatii, fiecare dintre ele corespunzand unei valori apartinand
unuia dintre cei trei parametri.
Este
momentul sa recurgem la considerente de natura fizica pentru a
gasi valorile corecte ale parametrilor necunoscuti. Exista
doua legi generale pe care le putem aplica :
T
conservarea masei de lichid
T
conservarea energiei mecanice
Din prima conditie
decurge ecuatia de continuitate :
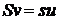
(u este viteza de
curgere in dreptul orificiului de sectiune s, iar v este viteza de
curgere la suprafata lichidului din rezervor).
Pentru a
aplica a doua conditie de natura fizica, vom considera un
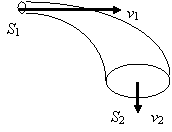
interval de timp foarte scurt dt. In
acest interval de timp, o cantitate de lichid dV trece prin orificiu, rezultatul fiind scaderea nivelului de
lichid din rezervor cu dh (vezi
si figura). Deoarece am facut ipoteza ca procesul de curgere
este ideal, rezulta ca energia mecanica se conserva. Deci,
energia mecanica a stratului de lichid de volum dV de la suprafata la inceputul intervalului de timp dt trebuie sa fie egala cu
energia mecanica a jetului de volum dV
format la baza rezervorului la sfarsitul intervalului de timp dt :
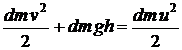
(termenul dm gh
reprezinta energia potentiala gravitationala
fata de nivelul de referinta care corespunde bazei rezervorului,
iar termenii care contin patratul vitezei reprezinta valorile
energiei cinetice). Rezulta :
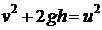
Eliminand viteza u
a jetului cu ajutorul ecuatiei de continuitate, obtinem :
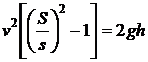
Notand S/s cu s si derivand in raport
cu timpul, rezulta :
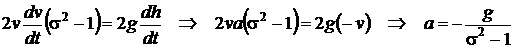
(dh/dt = -v rezulta din aceea ca dh este negativ (nivelul lichidului descreste) iar viteza de
curgere indreptata in jos este considerata pozitiva; faptul
ca acceleratia este negativa indica faptul ca orientarea
ei este inversa in raport cu orientarea acceleratiei
gravitationale sau cu orientarea vitezei de curgere, ceea ce arata
ca viteza de scurgere lichidului se micsoreaza in timp). Rezultatul obtinut arata ca
acceleratia este constanta, ceea ce inseamna ca
inaltimea lichidului din rezervor descreste dupa o lege
corespunzatoare miscarii uniform variate :
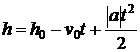
Aceasta relatie indica faptul ca
exponentul y din formula
obtinuta folosind metoda Rayleigh poate lua doar trei valori : 0, 1
si 2. Sa discutam aceste cazuri pe rand.
Cazul y = 0
Avem :
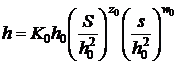
Parametrii z0
si w0 pot lua
inca valori arbitrare. De aceea, luand in consideratie toate valorile
posibile ale acestor parametri, putem scrie :
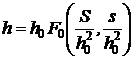
unde functia 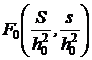 este necunoscuta.
Dar, asa cum rezulta din ecuatia determinata din
considerente fizice, termenul care nu depinde de timp trebuie sa fie constant
si egal cu h0.
Aceasta impune ca functia F0
sa fie constanta si egala cu 1.
este necunoscuta.
Dar, asa cum rezulta din ecuatia determinata din
considerente fizice, termenul care nu depinde de timp trebuie sa fie constant
si egal cu h0.
Aceasta impune ca functia F0
sa fie constanta si egala cu 1.
Cazul y = 2
Avem :
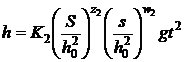
Parametrii z2
si w2 pot lua
inca valori arbitrare. De aceea, luand in consideratie toate valorile
posibile ale acestor parametri, putem scrie :
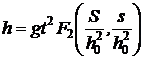
unde functia 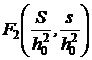 este necunoscuta.
Dar, asa cum rezulta din ecuatia determinata din
considerente fizice, termenul care depinde de patratul timpului trebuie
sa fie proportional cu o constanta care este :
este necunoscuta.
Dar, asa cum rezulta din ecuatia determinata din
considerente fizice, termenul care depinde de patratul timpului trebuie
sa fie proportional cu o constanta care este : 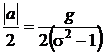 . Aceasta impune ca functia F2 sa fie constanta si egala cu
. Aceasta impune ca functia F2 sa fie constanta si egala cu 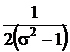 .
.
Cazul y = 1
Avem :
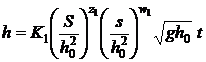
Parametrii z1
si w1 pot lua
inca valori arbitrare. De aceea, luand in consideratie toate valorile
posibile ale acestor parametri, putem scrie :
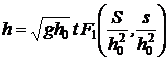
unde functia 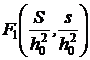 este necunoscuta.
Dar, asa cum rezulta din ecuatia determinata din
considerente fizice, termenul direct proportional cu timpul trebuie
sa fie proportional cu viteza initiala de curgere : v0. Folosind ecuatia lui
Galilei, si deoarece la sfarsitul timpului de scurgere viteza de
scurgere se anuleaza, obtinem :
este necunoscuta.
Dar, asa cum rezulta din ecuatia determinata din
considerente fizice, termenul direct proportional cu timpul trebuie
sa fie proportional cu viteza initiala de curgere : v0. Folosind ecuatia lui
Galilei, si deoarece la sfarsitul timpului de scurgere viteza de
scurgere se anuleaza, obtinem :
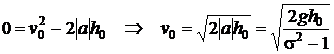
Concluzia este aceea ca functia F1 este egala cu : 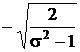 .
.
In final,
concluzia acestei analize este aceea ca ecuatia nivelului lichidului
este:
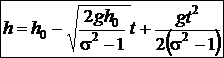
Experimental, va trebui sa determinam validitatea
acestei legi si sa calculam aria sectiunii rezervorului,
cunoscand aria orificiului de scurgere.
UMPLEREA
REZERVORULUI
Consideram
acelasi rezervor, prevazut cu orificiu de scurgere, alimentat
permanent cu lichid de o sursa cu debitul volumic D. In cazul ideal, considerentele fizice de care trebuie tinut
seama sunt aceleasi :
T
conservarea masei de lichid
T
conservarea energiei mecanice
Conditia de conservare a masei
conduce la ecuatia de continuitate :
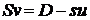
Conditia de conservare a
energiei mecanice se exprima prin relatia :
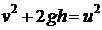
Eliminand viteza u
intre cele doua relatii, obtinem ecuatia :
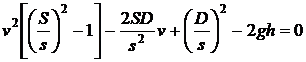
Exista doua posibilitati : fie debitul
este suficient de mare astfel incat nivelul lichidului sa
depaseasca inaltimea rezervorului, fie debitul are o
asemenea valoare incat, in timp, nivelul lichidului se stabilizeaza la o
anumita cota. In al doilea caz, viteza lichidului din rezervor, la
suprafata sa, se anuleaza (h
= const T v = 0). Din ecuatia anterioara obtinem
inaltimea maxima pe care o poate atinge lichidul :
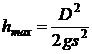
Experimental, se poate verifica validitatea acestei
relatii.
NOTA
Se poate
determina analitic, in conditiile amintite, relatia intre
inaltimea momentana a lichidului din rezervor si timp.
Expresia este :
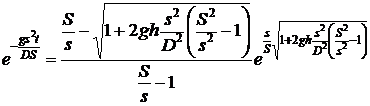
Dupa cum se poate remarca, inaltimea se
afla intr-o relatie destul de complicata cu timpul. Examinand
expresia, putem totusi remarca faptul ca, matematic vorbind, inaltimea
limita (maxima) nu se atinge decat dupa un timp infinit de lung.
Din punct de vedere practic, timpul de umplere este finit, valoarea sa
depinzand de gradul de precizie cu care putem masura inaltimea
lichidului din rezervor.
MATERIALE SI
APARATE
M
Programul
"GOLREZ"
M
Tehnica
de calcul necesara prelucrarii rezultatelor
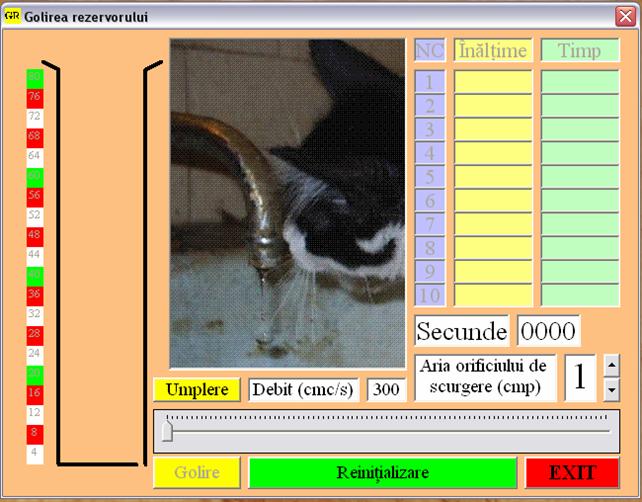
EXPLICATII : (1) control de incrementare-decrementare a
suprafetei orificiului de scurgere, (2) indicator de nivel, (3) slider pentru modificarea debitului de
alimentare cu lichid, (4) tabel de date care se completeaza efectuand un click pe indicatorul de nivel, (5)
mata care studiaza fenomenul.

MOD DE LUCRU
Se deschide programul "GOLREZ".
Se fixeaza valoarea 1 (cm2) cu ajutorul
controlului (1).
Se foloseste sliderul (3) pentru a stabili debitul. Se recomanda ca debitul
sa fie mare, astfel incat rezervorul sa se umple repede.
Se apasa butonul "Umplere" si se
urmareste cresterea nivelului lichidului pana la limita
superioara a cotei 56 de pe indicatorul de nivel (2). In momentul in care
s-a atins aceasta inaltime se apasa butonul "Stop".
Se apasa butonul "Golire"
Se urmareste nivelul lichidului. Cand
acesta trece prin dreptul limitei superioare al unei cote de pe indicatorul de
nivel se da un click pe cota
respectiva. Tabelul de date (4) se va completa automat cu valoarea
nivelului lichidului si cu momentul de timp corespunzator.
Dupa completarea tabelului, se noteaza
datele intr-o foaie "Excel"
Se apasa butonul "Reinitializare",
dupa care se reiau procedurile pana la completarea tabelului "DATE
EXPERIMENTALE ALE CURGERII"
Cu ajutorul programului "Excel" se fiteaza
datele, corespunzator unei functii polinomiale de gradul al doilea.
In total, in urma fitarii, trebuie obtinute 10 ecuatii (cate una
pentru fiecare suprafata a orificiului de scurgere 2
inaltimi initiale). Aceste ecuatii se trec in tabelul "LEGEA
CURGERII"
Se verifica daca media termenilor care
nu depind de timp este comparabila cu inaltimea
initiala
Se verifica daca coeficientii
termenului in t2 au valori
comparabile pentru valori egale ale ariei orificiului de scurgere si se
face media lor pentru fiecare valoare a ariei orificiului de scurgere
Stiind ca valoarea coeficientului lui t2 este 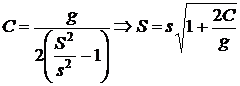 , se calculeaza S
cu ajutorul celor cinci valori medii calculate anterior (g = 981 cm/s2).
, se calculeaza S
cu ajutorul celor cinci valori medii calculate anterior (g = 981 cm/s2).
In final se calculeaza valoarea medie a lui
S si se trece in rubrica
corespunzatoare pe pagina "PRELUCRAREA DATELOR".
FACULTATIV : se verifica relatia 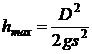 alegand o valoare
predeterminata a inaltimii maxime si calculand debitul
corespunzator, dupa care cu sliderul (3) se fixeaza aceasta
valoare a debitului si se urmareste umplerea rezervorului.
alegand o valoare
predeterminata a inaltimii maxime si calculand debitul
corespunzator, dupa care cu sliderul (3) se fixeaza aceasta
valoare a debitului si se urmareste umplerea rezervorului.

PRELUCRAREA
DATELOR
|
DATE EXPERIMENTALE ALE CURGERII
|
|
NC
|
Inaltime
initiala (cm)
|
Inaltime
initiala (cm)
|
|
56
|
76
|
|
Aria
orificiului de scurgere (cm2)
|
Aria
orificiului de scurgere (cm2)
|
|
1
|
2
|
3
|
4
|
5
|
1
|
2
|
3
|
4
|
5
|
|
h
(cm)
|
t
(s)
|
h
(cm)
|
t
(s)
|
h
(cm)
|
t
(s)
|
h
(cm)
|
t
(s)
|
h
(cm)
|
t
(s)
|
h
(cm)
|
t
(s)
|
h
(cm)
|
t
(s)
|
h
(cm)
|
t
(s)
|
h
(cm)
|
t
(s)
|
h
(cm)
|
t
(s)
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aria sectiunii transversale a
rezervorului
S = . . .. cm2
|
|
|
LEGEA
CURGERII
|
|
Inaltime initiala
(cm)
|
56
|
Aria orificiului de scurgere
(cm2)
|
1
|
|
|
2
|
|
|
3
|
|
|
4
|
|
|
5
|
|
|
Inaltime initiala
(cm)
|
76
|
Aria orificiului de scurgere
(cm2)
|
1
|
|
|
2
|
|
|
3
|
|
|
4
|
|
|
5
|
|
STUDENTI
1)
2)
3)
4)
5)
SEMNATURA CADRULUI DIDACTIC
|
|



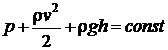

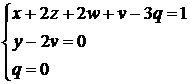
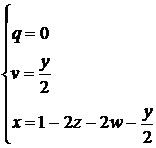
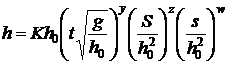
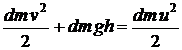
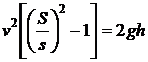
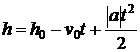
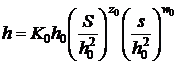
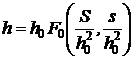
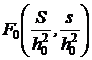 este necunoscuta.
Dar, asa cum rezulta din ecuatia determinata din
considerente fizice, termenul care nu depinde de timp trebuie sa fie constant
si egal cu h0.
Aceasta impune ca functia F0
sa fie constanta si egala cu 1.
este necunoscuta.
Dar, asa cum rezulta din ecuatia determinata din
considerente fizice, termenul care nu depinde de timp trebuie sa fie constant
si egal cu h0.
Aceasta impune ca functia F0
sa fie constanta si egala cu 1.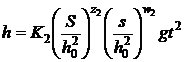
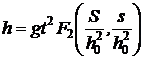
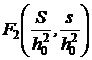 este necunoscuta.
Dar, asa cum rezulta din ecuatia determinata din
considerente fizice, termenul care depinde de patratul timpului trebuie
sa fie proportional cu o constanta care este :
este necunoscuta.
Dar, asa cum rezulta din ecuatia determinata din
considerente fizice, termenul care depinde de patratul timpului trebuie
sa fie proportional cu o constanta care este : 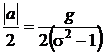 . Aceasta impune ca functia F2 sa fie constanta si egala cu
. Aceasta impune ca functia F2 sa fie constanta si egala cu 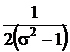 .
.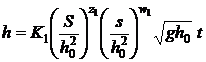
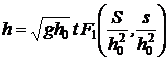
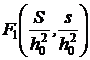 este necunoscuta.
Dar, asa cum rezulta din ecuatia determinata din
considerente fizice, termenul direct proportional cu timpul trebuie
sa fie proportional cu viteza initiala de curgere : v0. Folosind ecuatia lui
Galilei, si deoarece la sfarsitul timpului de scurgere viteza de
scurgere se anuleaza, obtinem :
este necunoscuta.
Dar, asa cum rezulta din ecuatia determinata din
considerente fizice, termenul direct proportional cu timpul trebuie
sa fie proportional cu viteza initiala de curgere : v0. Folosind ecuatia lui
Galilei, si deoarece la sfarsitul timpului de scurgere viteza de
scurgere se anuleaza, obtinem :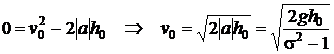
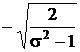 .
.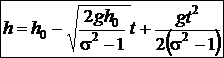

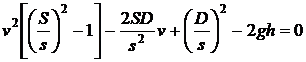
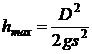
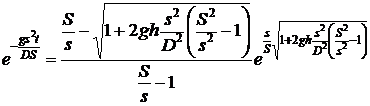


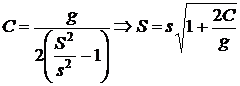 , se calculeaza S
cu ajutorul celor cinci valori medii calculate anterior (g = 981 cm/s2).
, se calculeaza S
cu ajutorul celor cinci valori medii calculate anterior (g = 981 cm/s2).