Stingerea arcului electric de curent continuu in
cazul circuitelor inductive
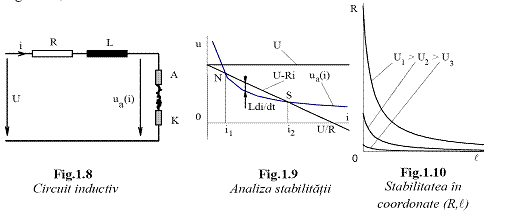
Se considera circuitul
R, L de curent continuu (Fig.1.8), la deconectarea caruia, intre
contactele A, K, se amorseaza un arc electric, pe coloana caruia se
inregistreaza tensiunea ua(i).
Ecuatia de regim tranzitoriu a acestui
circuit este de forma:

U fiind tensiunea continua de alimentare. Utilizand
functia de aproximare a Hertei Ayrton, pentru ecuatia (1.25) se
stabileste expresia:

fiind
constante, iar l-lungimea
coloanei arcului electric. In cazul arderii stationare, la curent constant
a arcului electric, ecuatia (1.26) devine algebrica, de forma:
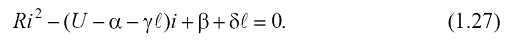
Din analiza acestei
ecuatii, rezulta unele concluzii privind stabilitatea arderii arcului
electric, intr-un circuit inductiv de curent continuu. Ecuatia (1.27)
poate admite doua solutii reale, pozitive si distincte, i1 i2, caz in care circuitului din Fig.1.8 ii sunt proprii doua
puncte de functionare; fie acestea N si S (Fig.1.9), determinate la
intersectia dreptei de sarcina (U-Ri)
cu caracteristica volt-amper, ua(i), a arcului electric. Punctul de functionare N corespunde
arderii instabile deoarece, la mici variatii ale intensitatii
curentului in jurul valorii i1, rezulta tendinte de variatie divergente in
raport cu i1 (pentru i>i1
se obtine di/dt>0, deci o tendinta de crestere a
intensitatii, in timp ce pentru i<i1,
rezulta di/dt<0, deci tendinta de scadere a
intensitatii curentului). In acelasi mod se poate arata
ca punctul S corespunde arderii stabile a arcului electric, deoarece la
variatii ale curentului in jurul valorii i2, rezulta tendinte de variatie convergente spre i2.. In regim static, deci la variatii cu viteze di/dt oricat
de mici ale intensitatii curentului, cand tensiunea autoindusa
pe bobina poate fi neglijata, conditia necesara pentru stingerea
arcului electric, Fig.1.9, se poate scrie sub forma:

Pentru aceasta este necesar
ca ecuatia (1.27) sa admita cel mult o radacina
dubla sau radacini complexe, ceea ce revine la a scrie:
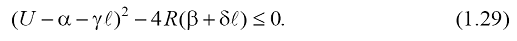
Inecuatia (1.29)
delimiteaza domeniul, in planul coordonatelor (R, l , corespunzator caruia stingerea arcului electric
este, in acest caz, sigura. In Fig.1.10 sunt reprezentate, conform
ecuatiei (1.29), granitele zonelor de ardere a arcului electric,
pentru diferite valori ale tensiunii de alimentare a circuitului considerat.
Arcul electric arde, eventual stabil, pentru valori (R, l definind puncte localizate in zona dintre axele de coordonate
si curbele de granita si poate fi stins, pentru dublete (R, l specifice unor puncte din afara acestei zone. Pentru puncte de
functionare (R, lcr) situate pe curbele (1.29), arderea arcului electric este
critica (punctele N, S, Fig.1.9, se confunda). Conditia (1.28)
poate fi indeplinita fie prin alungirea coloanei, fie prin cresterea
rezistentei R, fie printr-un procedeu combinat. In cazul stingerii arcului
prin alungirea coloanei, pentru intensitatea icr
se obtine:

Alungirea
coloanei conduce la cresterea tensiunii de arc, fapt care conduce la
deplasarea pe verticala a caracteristicii volt-amper, pana la
indeplinirea conditiei de stingere, adica pana cand aceasta
ajunge sa fie amplasata deasupra dreptei de sarcina. In cazul
deconectarii dinamice, concluzii corecte sub raport calitativ pot fi
obtinute pe cale analitica in ipoteza simplificatoare a
neglijarii fenomenului de histerezis, propriu caracteristicilor dinamice
ale arcului (Fig.1.5b). In aceste conditii, considerand ca viteza v, de alungire a arcului, este constanta, ecuatia
diferentiala (1.26) se poate scrie sub forma:

Impunand conditia ta>0, din relatia (1.36) se obtine:

 evidentiindu-se
astfel ca stingerea arcului electric de curent continuu este posibila
numai daca lungimea coloanei acestuia depaseste o valoare
limita. Regimul tranzitoriu al curentului prin coloana arcului electric
este reprezentat in Fig.1.11.
evidentiindu-se
astfel ca stingerea arcului electric de curent continuu este posibila
numai daca lungimea coloanei acestuia depaseste o valoare
limita. Regimul tranzitoriu al curentului prin coloana arcului electric
este reprezentat in Fig.1.11.
Se poate concluziona ca atat durata de
ardere, cat si lungimea maxima a arcului electric au valori
dependente de constanta
de timp a circuitului deconectat si sunt cu atat mai mari, cu cat
caracterul acestuia este mai inductiv. Prelungirea duratei de ardere a arcului
are loc pe seama energiei acumulate in campul magnetic al bobinelor din
circuit, tensiunea autoindusa pe acestea, la scaderea
intensitatii curentului, suplimentand tensiunea sursei de alimentare.





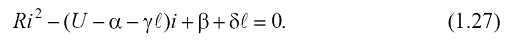



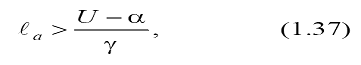 evidentiindu-se
astfel ca stingerea arcului electric de curent continuu este posibila
numai daca lungimea coloanei acestuia depaseste o valoare
limita. Regimul tranzitoriu al curentului prin coloana arcului electric
este reprezentat in Fig.1.11.
evidentiindu-se
astfel ca stingerea arcului electric de curent continuu este posibila
numai daca lungimea coloanei acestuia depaseste o valoare
limita. Regimul tranzitoriu al curentului prin coloana arcului electric
este reprezentat in Fig.1.11.