Modele pentru reprezentarea si
conceptualizarea unui proces de afaceri
Prin modelare intelegem un demers
stiintific bazat pe diferite teorii, metode, discipline, demers ce
trebuie sa conduca la sporirea gradului de cunoastere intr-un
domeniu si care se finalizeaza cu un model.
Putem afirma ca modelarea
proceselor de afaceri este folosita de manageri ca o alternativa la
experimentele facute in cazul stiintelor exacte.
Modelul este o reprezentare izomorfa a realitatii
care ofera o imagine intuitiva, dar riguroasa, in sensul structurii
logice a fenomenului studiat si permite descoperirea unor legaturi
greu de stabilit pe alte cai.
Modelarea
nu este un scop in sine. Importanta practica a oricarui model
deriva din accesibilitatea
subiectului cercetarii la obiectul respectiv. Daca analiza modelului (prin
experiment sau cercetare deductiva) este mai accesibila subiectului
decat studierea nemijlocita a obiectului, atunci modelul
isi justifica existenta.
Imaginea
care se creaza in mintea subiectului trebuie sa fie homomorfa cu
obiectul, adica sa stabileasca o corespondenta univoca
intre caracteristicile obiectului si imaginea sa (de exemplu un teren
si harta lui). Dupa obtinerea imaginii homomorfe simplificate a
obiectului, subiectul construieste modelul propriu-zis: un sistem abstract
sau material, izomorf cu imaginea simplificata formata
anterior.
Procesul
general de modelare se desfasoara dupa schema urmatoare:
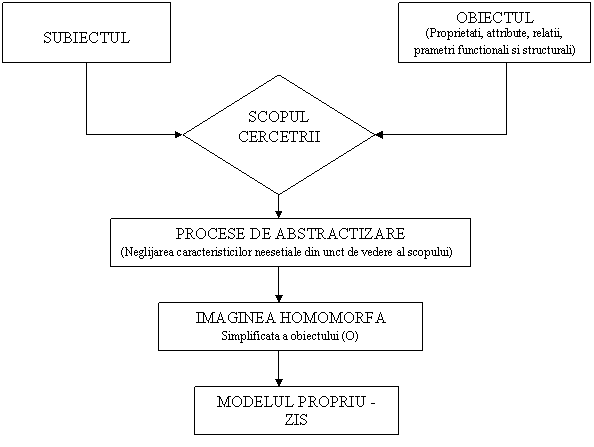
Fig. 2 - Desfasurarea
procesului general de modelare.
Exista
numeroase definitii si clasificari ale modelelor. Termenul ca
atare se pare ca a fost folosit pentru prima data de matematicianul
Beltrami in 1868, provenind de la radacina latina 'modus', care, printre
altele, inseamna si 'mijloc'. Definitia cea mai generala
considera modelul ca o reprezentare simplificata (materiala
sau simbolica) a realitatii obiective (uneori a unei
teorii abstracte) care se subordoneaza scopului cercetarii.
Modelul
este un obiect sau un dispozitiv creat artificial de om care seamana intr-o
anumita masura cu altul (acesta din urma fiind un obiect de
cercetare sau de interes practic). Notiunea de model se refera la un
mod de cunoastere a realitatii care consta in reprezentarea
fenomenului studiat cu ajutorul unui sistem construit artificial.
Proprietatea
cea mai generala a unui model consta in capacitatea de a reflecta, de
a reproduce lucruri si fenomene ale lumii reale, ordinea lor necesara,
structura lor. Notiunea de model reiese din existenta unei
semanari (similitudini) intre doua obiecte - unul fiind considerat
originalul, celalalt modelul sau. Se cerceteaza prin analogie un
sistem, iar concluziile se refera la alt sistem. In acest caz sistemul
cercetat este o reflectare (un model) al originalului.
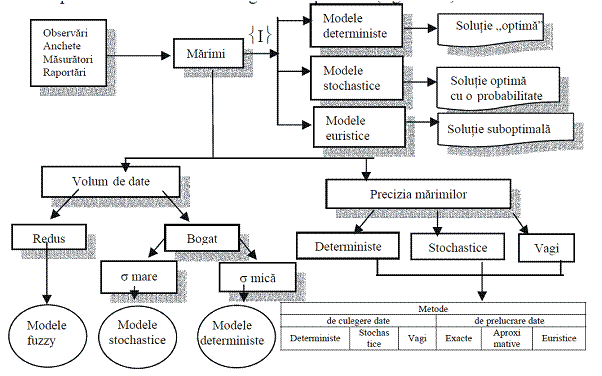
Fig. 3 - Procesul modelarii
Notiunea de model este o notiune
metodologica generala. Prin model se intelege constructia
reala sau imaginata a oricarui obiect, fenomen, proces care
reflecta trasaturile esentiale ale obiectului cercetat.
Tipologia
modelelor
Complexitatea
si diversitatea lumii reale au condus la elaborarea unor modele foarte
variate. Sistematizarea multitudinii de modele elaborate se face pe baza mai
multor criterii. Astfel, daca se ia in considerare natura fizica a
elementelor modelului (mijloacele prin care se reproduc obiectele studiate), modelele
pot fi:
a) modele fizice (materiale,
tehnice);
b) modele abstracte (conceptuale,
imaginate, ideale);
c) modele hibride.
Modelele fizice (materiale, tehnice) contin elemente de natura fizica.
Ele sunt create de om, dar exista obiectiv, independent de vointa lui,
ele fiind materializate. Acestea reproduc, in scop cognitiv, obiectul studiat
pentru a-i reda structura sau unele proprietati. Modelul fizic poate
pastra natura fizica a obiectului sau asemanarea geometrica
cu acesta.
Cand
proprietatile obiectului sunt exprimate prin ele insele, dar la alta
scara, avem de a face cu modele fizice imitative. Un model
imitativ seamana cu obiectul pe care-l reprezinta, dar difera ca
marime. Sunt de obicei modele specifice, concrete si greu de
manipulat in scopuri experimentale (machete de avion, nave, scheme
electronice).
Cand
se folosesc anumite proprietati pentru a reprezenta alte proprietati,
modelele fizice sunt analogice. De exemplu, inaltimile
se reprezinta pe harta prin linii orizontale, graficele sunt modele
analogice care, utilizand proprietati geometrice (distanta,
pozitie), exprima o varietate de elemente si relatii intre
ele. Modelele analogice sunt mai putin specifice, mai putin concrete si
mai usor de manuit decat cele imitative.
Modelele abstracte (conceptuale, imaginate, ideale) reprezinta imagini ale obiectului
real si descriu proprietatile esentiale intr-un limbaj simbolic
(matematic). Ele nu au nimic comun cu natura obiectului cercetat, ci reflecta
realitatea in plan gnoseologic, pe baza izomorfismului cu aceasta realitate.
Reproducerea obiectului studiat este simplificata, constituind o
anumita idealizare a realitatii. Spre deosebire de modelele
fizice, modelele abstracte folosesc litere, numere, alte simboluri pentru a
reprezenta elemente variabile si legaturile dintre ele. Sunt cele mai
generale, cu ele se lucreaza experimental usor si, de obicei, iau
forma unor relatii matematice.
Modelele abstracte se pot clasifica la randul
lor in: modele abstracte cantitative si modele abstracte calitative.
Cele cantitative se mai numesc si numerice, fiind descrise prin relatii
matematice particularizate (parametrii au valori numerice concrete). Asa
sunt, de exemplu, modelele econometrice.
Cele
calitative (se numesc si logice, grafice) includ numai specificarea
formei relatiilor si sunt reprezentabile prin scheme, diagrame, forme
grafice.
Modelele hibride cuprind atat elemente fizice, cat si elemente abstracte. Ele
presupun interactiunea dintre un sistem format din elemente fizice si
un calculator electronic numeric programat corespunzator.
Daca
se are in vedere modul de reflectare a caracteristicilor obiectului, se
disting:
a) modele normative;
b) modele descriptive.
Modelele pot reflecta atat
structura interna a obiectului, cat si relatiile dintre elementele
sale. Cand structura interna nu este accesibila cercetarii, modelul
reflecta numai comportamentul sau, functionarea acestuia,
determinand dependenta dintre actiunile asupra obiectului si
starile sale. Modelele la construirea carora se urmareste
determinarea unei asemenea stari a obiectului care sa fie cea mai buna,
iintr-un anumit sens, sau cea mai acceptabila din punct de vedere al
subiectului se numesc modele normative. Modelele destinate sa
explice faptele observate sau sa asigure prognoza comportamentului
obiectului se numesc modele descriptive. Modelele normative raspund
la intrebarea 'cum trebuie sa fie?', iar cele descriptive la
intrebarile 'cum este ?' sau 'cum va fi ?'.
Orice model, deci si un model
economico-matematic, trebuie sa fie izomorf cu imaginea simplificata a
obiectului cercetat, care la randul sau este homomorfa cu obiectul. Din
acest motiv deosebim doua nivele ale tipologiei modelelor
economico-matematice.
La
un prim nivel, criteriile de clasificare caracterizeaza gradul de simplificare
constienta a obiectului real in imaginea sa (homomorfismul), iar la al
doilea nivel, criteriile caracterizeaza deosebirile dintre modele ca
scheme matematice care asigura izomorfismul modelului cu imaginea
simplificata.
Astfel,
la primul nivel, deosebim criteriile:
A. Dupa profunzimea cuprinderii
organizarii structurale si a functiilor obiectului:
modele ale structurii tehnologice;
modele ale structurii institutional (organizatorice);
modele ale structurii sociale si ale mediului.
B. Dupa modul de formalizare:
modele generale (agregate);
modele particulare (detaliate).
C. Dupa finetea redarii proprietatilor si
relatiilor structurale ale obiectului:
modele deterministe;
modele probabiliste (stochastice);
modele de risc si incertitudine;
modele statistice.
D. Dupa natura matematica a relatiilor:
modele liniare;
modele neliniare.
Modelele
particulare pot fi localizate dupa o caracteristica functionala,
dupa structura (modelul unei celule economice) sau dupa timp (modele
statice, dinamice). Modelele deterministe cuprind exclusiv functii
matematice particularizate, in care nu intervin variabile aleatoare. Cele
probabilistice (stochastice) implica utilizarea variabilelor aleatoare. Un
caz particular il reprezinta modelele fuzzy (vagi) care reflecta
imprecizia sistemului studiat si permit stabilirea gradului de apartenenta
la o anumita proprietate. Adesea se intalnesc si modele mixte care
includ atat variabile aleatoare cat si deterministe.
Cand
se analizeaza 'miscarea' diferitelor elemente (variabile)
ale modelului, intervin modelele de risc si incertitudine. Daca o
modificare a unui element produce o consecinta precisa suntem intr-o
situatie certa. Probabilitatea producerii consecintei respective
este egala cu 1. Cand probabilitatea producerii consecintei este diferita
de 1, dar se cunoaste sau poate fi estimata, suntem intr-o situatie
de risc. Riscul provine din faptul ca, desi probabilitatea aparitiei
consecintei modificarii, nu cunoastem momentul si locul
aparitiei. Exista, deci, riscul unor situatii nedorite. Este
posibil insa sa nu cunoastem probabilitatea aparitiei
consecintei unei modificari si nici nu putem sa o
estimam. Aceasta este situatia de incertitudine. Modelele statistice
cuprind cel putin o relatie dedusa prin prelucrarea statistica
a datelor experimentale (relatii functionale empirice).
La
al doilea nivel al tipologiei criteriile sunt:
A. Dupa conceptia de
formalizare:
modele construite dupa principiul finalist;
modele construite dupa principiul mecanic;
modele construite dupa principiul sistemic.
B. Dupa raportul dintre
parametri endogeni si exogeni:
modele deschise;
modele inchise.
C. Dupa tipul de variatie
al variabilelor:
modele cu variabile continue;
modele cu variabile discrete;
modele de tip mixt.
D. Dupa obiectul cercetarii:
modele macroeconomice;
modele microeconomice.
Studiu
de caz: modelul producatorului
Limitandu-ne
la o realitate pur economica, putem afirma ca agentul producator
(intreprinderea) este o unitate, mai mult sau mai putin complexa,
care pune in lucru diversi factori de productie (input-uri) pentru a
furniza, in cele mai bune conditii, bunuri si servicii (output-uri)
rezultate din transformarea factorilor de productie utilizati:
factorii de productie
(input-urile) sunt, in esenta, de trei categorii: bunuri fungibile,
care dispar sau isi schimba natura in procesul de transformare; munca
umana sub diversele ei forme; serviciile date de bunurile de productie
durabile.
.
bunurile si serviciile produse (output-urile) pot corespunde fie
bunurilor si serviciilor de consum final, fie bunurilor de productie
utilizate ca intermediar de alte intreprinderi pentru a produce alte bunuri.
transformarea factorilor de productie
poate fi inteleasa in diferite sensuri. In mod obisnuit, prin transformare se intelege
a 'elabora' un bun, a-1 face capabil sa satisfaca o nevoie.
Dar, la fel de bine, a transforma iseamna si a face disponibil,
intr-un loc dat si la un moment dat, un bun. Activitattile
de transport si stocare sunt considerate activitati de
productie. Transformarea trebuie sa se faca 'in cele mai bune conditii',
atat in sens tehnic, cat si economic.
Din
punct de vedere tehnic, daca o productie reclama utilizarea a n
factori de productie si pentru a produce un nivel dat de output avem
de ales intre doua tehnici care presupun utilizarea cantitatilor
a1,a2,,an, respectiv a'1,a'2,,a'n,
cu ai< a'i pentru orice i,
cel
putin o inegalitate fiind stricta, este evident ca vom alege prima
varianta.
Daca
nu se procedeaza asa, inseamna ca se accepta o anumita
risipa, sau, altfel spus, nu se produce in cele mai bune conditii
tehnice. Problema devine economica atunci cand trebuie ales intre cele doua
colectii de input-uri ai si a'i, dar
inegalitatile nu sunt verificate pentru toti i. In acest
caz, pentru a putea efectua alegerea intervine notiunea de cost.
Vom
defini procesul de productie ca un sir de N numere reale, adica un
punct in spatiul bunurilor. Procesul de productie A va fi
definit prin vectorul [ai]. Se adopta conventia de a nota
pozitiv bunurile produse (output-urile) si negativ factorii de productie
(input-urile). In ipoteza ca nu poate exista productie plecand de la
nimic, adaugam ca cel putin o componenta a vectorului este
negativa. Prin extensie, vectorul [0] consta in procesul de
productie denumit 'a nu face nimic'.
Sa
presupunem, de exemplu, ca exista trei bunuri: pamant (masurat in
ha), munca (ore) si grau (kg). Daca vrem sa producem 3000 kg grau
pornind de la 1 ha teren si 275 ore munca, procesul de productie este
reprezentat prin vectorul [-1, -275, +3000] ϵ R3. Adesea un
proces de productie are componente nule. Daca in exemplul anterior adaugam
un al patrulea bun, de exemplu, struguri, procesul corespunzator productiei de
grau va fi [-1, -275, +3000, 0] ϵ R4.
Spunem
ca un proces de productie este posibil daca exista
cunostintele tehnice, la un moment dat, pentru a realiza procesul. Aici
intervine doar limita tehnica. Limitarile datorate raritatii
factorilor de productie nu intervin, in general, in notiunea de
proces de productie posibil. In unele cazuri, putem insa vorbi de
procese de productie posibile, fixand, apriori unii factori de productie.
De exemplu, nu este lipsit de sens de a vorbi de multimea de procese de
productie posibile pentru o intreprindere de 300 ha, adica pentru o intreprindere
unde factorul de productie 'pamant' este fixat la un anumit
nivel. In definirea multimii proceselor de productie posibile pentru
o intreprindere data este recomandabil sa se precizeze care sunt factorii ficsi
si care sunt cei care variaza.
Presupunem
acum ca in economie sunt J intreprinderi, reperate prin indicele j=1,2,,J.
Fie a si b complexele de bunuri reprezentand respectiv
input-urile (ak) si output-urile (b) ale intreprinderii
j. Diferenta y=ti-d este 'productia neta' a
producatorului j. Ea este pozitiva daca bunul k este un output,
respectiv negativa, daca acesta este un input.
Notam
cu y vectorul de componente yk si cu multimea
proceselor de productie posibile pentru producatorul j. Restrictiile
tehnice de productie vor fi redate fie prin yϵ Y1, fie
apeland la un concept mai limitat, cel de 'functie de productie':
(y)=0. in continuare renuntam la specificarea indicelui j.
Asupra
multimii Y se fac urmatoarele ipoteze:
Ipoteza
1 (aditivitatea).
Daca doi vectori y1, y2 definesc productii
posibile (y1 ϵY, y2 ϵ Y), atunci
vectorul y=y1 +y2 defineste o productie
posibila (y e Y).
Ipoteza
2 (divizibilitatea).
Daca vectorul y defineste o productie posibila (y1
ϵ Y)si a este un numar cuprins intre 0 si 1,
atunci vectorul ay defineste de asemenea o productie posibila
(ay e Y).
Ipoteza
3 (randamente
de scara constante). Daca vectorul y1 defineste o
productie posibila (y1e Y) si daca
B este un numar pozitiv, atunci vectorul By defineste,
de asemenea, o productie posibila (B y1 ϵ Y).
Ipoteza
4 (convexitatea).
Daca vectorii y1 si y2 definesc productii
posibile si daca a este un numar cuprins intre 0 si 1, atunci
vectorul ay1 +(1-a)y2 defineste o productie
posibila.
Admitem
acum ca producatorul cauta sa maximizeze valoarea
'productiei nete' reprezentand diferenta intre valoarea
colectiilor de bunuri output si input, expresia anterioara poate fi
interpretata drept 'profit' (evident, este vorba despre profit
economic, nu contabil). Cel mai bun comportament al producatorului va consta,
deci, in maximizarea profitului. Prin urmare, modelul general al producatorului
se scrie astfel:
Max py sau Max py ye



