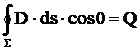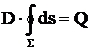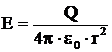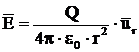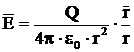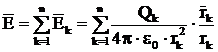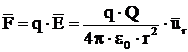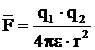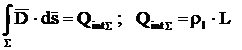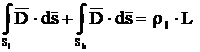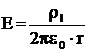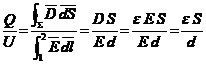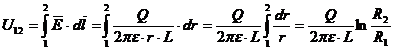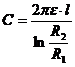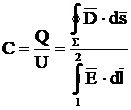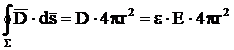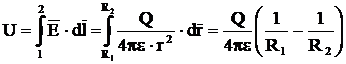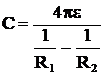Aplicatii ale legii
fluxului electric. Campul electric al unei sarcini punctiforme. Campul electric
al conductorului rectiliniu, infinit lung.
Campul electric al unei
sarcini punctiforme.
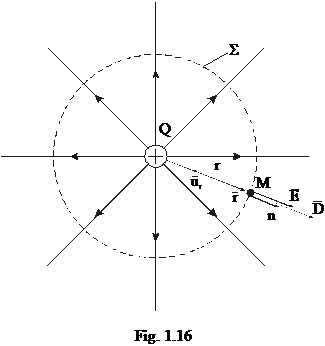
Fie o
sarcina electrica punctiforma Q pozitiva, situata in
vid.
 Ne
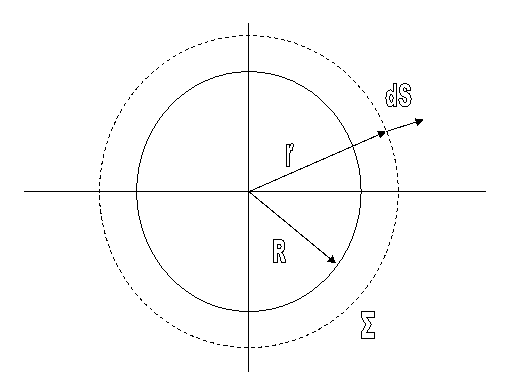
propunem sa determinam intensitatea cậmpului electric in punctul M aflat la distanta r .
Ne
propunem sa determinam intensitatea cậmpului electric in punctul M aflat la distanta r .
Se alege
o suprafata  inchisa ce trece
prin punctul dat si are o simetrie fata de sarcina Q data -
sfera cu centrul in Q.
inchisa ce trece
prin punctul dat si are o simetrie fata de sarcina Q data -
sfera cu centrul in Q.
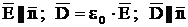
Din legea fluxului
electric:
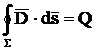 ;
;
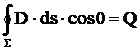
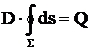
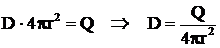
Intensitatea
campului electric este
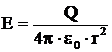
sau vectorial: 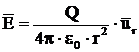
unde 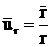 si rezulta:
si rezulta:
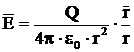
Pentru
cazul a n sarcini punctiforme 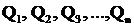 vom avea:
vom avea:
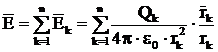
Daca in puntul M se aseaza o alta
sarcina q, atunci campul electric creat de Q in M va exercita o forta
asupra sarcinii q:
Aceasta este formula fortei ce se exercita
intre doua sarcini electrice punctiforme aflate in vid si situate la
o distanta r una fata de cealalta, numita si
formula lui Coulomb.
In alt
mediu decat vidul apare permitivitatea mediului 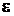 :
:
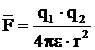
iar
forta 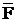 va scadea de εr ori
va scadea de εr ori
Campul electric al
conductorului rectiliniu, infinit lung.
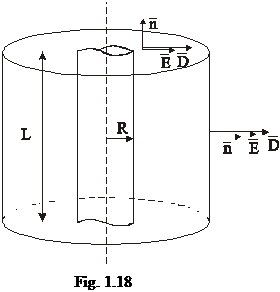
Consideram
un conductor de raza R avand axa perpendiculara pe figura, in
figura fiind reprezentata sectiunea circulara a
conductorului. Fie densitatea de linie ρl a sarcinii pe conductor.
Se
considera un cilindru 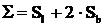 inchis unde
inchis unde 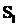 este suprafata
laterala iar
este suprafata
laterala iar 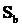 este suprafata
bazei.
este suprafata
bazei.
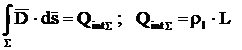
atunci: 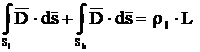
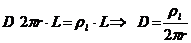
iar: 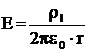
1.6 Conductoare in regim electrostatic
Regimul
electrostatic presupune ca sarcinile electrice sunt fixe in spatiu
si constante in timp.
Corpurile
conductoare metalice se caracterizeaza, din punct de vedere microscopic,
prin faptul ca poseda purtatori mobili de sarcina electrica,
electronii liberi din conductor. Daca in interiorul corpului conductor
exista camp electric de intensitate 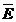 atunci electronii
liberi se misca prin conductor si conditia de echilibru
electrostatic nu se mai respecta. Pe baza celor mentionate
rezulta urmatoarele consecinte privind comportarea corpurilor
conductoare (metalelor) in regim electrostatic:
atunci electronii
liberi se misca prin conductor si conditia de echilibru
electrostatic nu se mai respecta. Pe baza celor mentionate
rezulta urmatoarele consecinte privind comportarea corpurilor
conductoare (metalelor) in regim electrostatic:
intensitatea
campului electric este nula in interiorul conductorului,
potentialul
electric este constant in interiorul conductorului
suprafata
conductorului este echipotentiala
nu
exista sarcini electrice in interiorul conductoarelor, sarcinile electrice
sunt repartizate doar la suprafata conductorului
intensitatea
campului electric este perpendiculara pe suprafata conductorului
efectul
de ecranare: in interiorul unei cavitati dintr-un material conductor
intensitatea campului electric este nula
1.7 Condensatorul. Capacitatea
electrica
Se numeste condensator sistemul fizic format
din doua corpuri metalice , numite armaturi, separate intre ele prin
materiale electroizolante si incarcate cu sarcini electrice egale
si de semne contrare.
La incarcarea
condensatorului cu sarcinile electrice Q1 = +Q si Q2
= -Q, cele doua armaturi vor avea potentialele V1
si V2 iar tensiunea dintre armaturi va fi U12.
Modificậnd sarcina electrica de pe armaturi la valoarea Q'
si tensiunea dintre armaturi se modifica si devine U12'.
Pentru orice
condensator avem relatia :
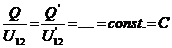 [F]
[F]
C, capacitatea
condensatorului
F, farad; 1µF = 10-6F, 1nF = 10-9F, 1pF = 10-12F
Se vorbeste
uneori despre capacitatea unui conductor; in acest caz trebuie sa
consideram armatura a doua la infinit, iar potentialul acesteia
nul V2 = V∞ = 0.
1.8
Capacitatea unor condensatoare simple
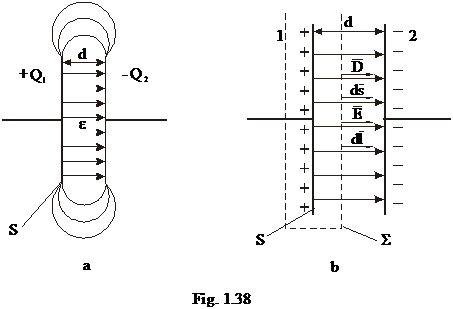
Capacitatea condensatorului plan
Condensatorul plan are doua armaturi
egale, plane si paralele, separate intre ele printr-un material
izolant (dielectric) liniar si omogen de permitivitate ε .
Daca distanta dintre armaturi este foarte mica se poate
neglija efectul de margine, iar intensitatea campului electric are aceeasi
valoare in toate punctele din tre armaturi, campul electric este uniform.
Valoarea
capacitatii se poate calcula astfel:
C = 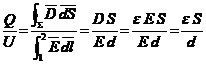
Pentru calculul
lui Q s-a aplicat legea fluxului electric pentru o suprafata
inchisa Σ de forma unui paralelipiped ce contine in interior
armatura pozitiva, iar pentru calculul tensiunii s-a calculat
integrala intensitatii campului electric pe o dreapta ce
uneste cela doua armaturi.
Capacitatea condensatorului cilindric.
Condensatorul
cilindric este format din doua armaturi cilindrice, coaxiale , de
raze R1 si R2 intre care se afla un dielectric
(material electroizolant) de permitivitate ε
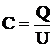 ;
;
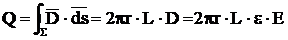
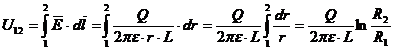
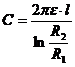
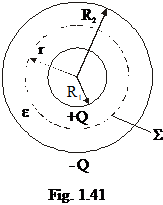
Capacitatea condensatorului sferic
Condensatorul
sferic este format din doua armaturi sferice, concentrice, de raze R1
si R2. Intre armaturi se afla un material dielectric
de permitivitate 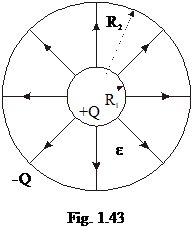
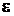
Capacitatea
se calculeaza astfel:
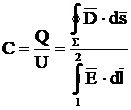
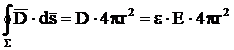
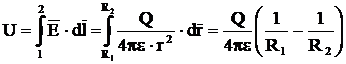
Capacitatea condensatorului sferic
devine:
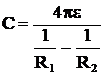
Pentru 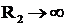 rezulta
rezulta
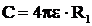
ceea ce
reprezinta capacitatea unei sfere de raza R1 in raport cu
infinitul aflata intr-un dielectric de permitivitate ε


 Ne
propunem sa determinam intensitatea cậmpului electric in punctul M aflat la distanta r .
Ne
propunem sa determinam intensitatea cậmpului electric in punctul M aflat la distanta r . 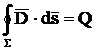 ;
;