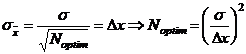DESPRE
ERORI IN FIZICA
1.
Introducere
Masurarea
unei marimi fizice este insotita de erori. Prin eroare nu intelegem "neatentia"
sau "greseala", ci, o imprecizie pe care nu o putem evita atunci cand efectuam
o masurare. Sunt si masurari neafectate de erori, cum ar fi numarul de studenti
din laborator la un moment dat. Pe de alta parte, numarul de molecule de aer
din laborator este imposibil de specificat in mod exact. Deoarece, de obicei
masuram marimi de acest al doilea tip, trebuie sa stim sa calculam imprecizia
masuratorilor noastre.
Pentru a exemplifica
importanta cunoasterii erorilor de masura vom cosidera urmatorul exemplu: sa
presupunem ca doriti sa cumparati o biblioteca pentru sufrageria apartamentului
vostru si rugati un prieten sa masoare inaltimea camerei. El va spune ca
inaltimea este de 300 cm. Atunci, comandati o biblioteca, din piese detasabile,
de 298 cm si cand o aduceti acasa constatati ca nu incape, pentru ca, de fapt,
gasiti ca sufrageria are 297 cm inaltime. Ce s-a intamplat? Prietenul nu v-a
spus ca a folosit pentru masurare o rigla scurta si eroarea a fost de  5 cm. In inginerie, in constructii, sau in medicina, o astfel
de eroare ar fi putut avea consecinte dramatice.
5 cm. In inginerie, in constructii, sau in medicina, o astfel
de eroare ar fi putut avea consecinte dramatice.
In
general erorile sunt de doua tipuri:
sistematice;
intamplatoare.
Erorile sistematice au mereu acelasi
semn si nu dispar prin medierea asupra unui numar mare de masuratori. Apar
erori sistematice cand masuram lungimea cu o rigla gradata incorect, cand
masuram timpul cu un ceas care ramane in urma, sau masuram diferenta de
potential cu un voltmetru incorect calibrat. De asemenea, erorile sistematice
pot aparea datorita experimentatorului, care, de exemplu, priveste incorect
scala aparatului de masura: in loc sa priveasca perpendicular acul
instrumentului de masura, privirea cade oblic, influentand rezultatul citirii.
Nu putem determina erorile sistematice intr-un singur experiment. Pentru
determinarea lor ar trebui sa masuram aceeasi marime fizica prin metode
diferite si apoi sa comparam rezultatele. Spunem ca un experiment are un grad
inalt de acuratete, daca erorile
sistematice sunt foarte mici.
Erorile intamplatoare pot avea
nenumarate si impredictibile cauze: fluctuatii ale presiunii si ale
temperaturii aerului din camera, ale tensiunii electrice de la sursa de energie
electrica, raze cosmice, etc. Deoarece ele apar cu egala probabilitate, atat cu
semnul minus cat si cu semnul plus, prin metode statistice putem estima aceste
erori intamplatoare. Despre experimentele cu erori intamplatoare mici spunem ca
sunt foarte precise.
2.
Erorile
facute la citirea scalei unui instrument de masura
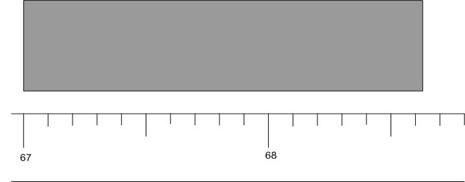
De
multe ori masuram cu instrumente care au o scala marcata. In exemplul din
figura de mai sus, lungimea obiectului (o radiera) este specificata de pozitia
capatului din dreapta. Acesta este situat mai aproape de diviziunea 68.6 cm
decat de diviziunea 68.7 cm. De aceea vom exprima lungimea: L = 1.6 ± 0.1 cm,
unde 1.6 cm este valoarea centrala si 0.1 cm este eroarea.
3.
Erorile
instrumentelor digitale
Instrumentele
moderne de laborator prezinta afisaje digitale. De exemplu un higrometru
electronic prezinta umiditatea relativa a aerului din camera: 753
%, aceasta fiind valoarea centrala a marimii masurate. Eroarea in
acest caz este data de limita de precizie a aparatului, precizata de producator
in documentele care insotesc aparatul la cumparare. Daca ne lipseste aceasta
informatie folosim urmatoarea regula: eroarea unui instrument electronic este,
de obicei, jumatate din ultimul digit de precizie. In exemplul descris mai sus
umiditatea relativa este cuprinsa intre 7525 % si 7535 %
. Rezultatul va fi pus sub forma: RH = 75.3 ± 0.05 %.
4.
Deviatia
standard
Sa
presupunem ca masuram perioada de oscilatie a unui pendul folosind un
cronometru. Eroarea cronometrului se poate estima asa cum am discutat mai
devreme. Totusi sursa principala de eroare consta in timpul de reactie pe
care-l avem la pornirea si oprirea cronometrului. Pentru a estima aceasta sursa
de erori solutia este sa masuram de mai multe ori aceasta perioada, valoarea
medie a acestor masuratori repetate fiind mult mai probabil aproape de valoarea
exacta decat ceea ce obtinem dupa o singura masuratoare.
Sa presupunem ca am masurat
perioada de oscilatie de cinci ori, obtinand valorile din tabelul urmator:
|
Numarul
masuratorii
|
1
|
2
|
3
|
4
|
5
|
|
Valoarea
masurata, ti (s)
|
4.9
|
4.5
|
4.7
|
4.5
|
4.4
|
|
Deviatia
(eroarea absoluta),  (s) (s)
|
0.3
|
-0.1
|
0.1
|
-0.1
|
-0.2
|
Cea mai buna estimare a
perioadei de oscilatie este valoarea medie a celor cinci valori
masurate:
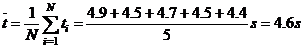
unde N = 5 reprezinta numarul de
masuratori (in cazul legii normale (Gauss) valoarea medie poate fi luata
eventual ca valoare de referinta acceptata, constituind un substitut al
asa-numitei "valori adevarate" a masurandului, care este in cele mai multe cazuri
necunoscuta ).
Am putea calcula eroarea ca
diferenta dintre cea mai indepartata valoare de valoarea medie si valoarea
medie: (4.9 - 4.6) s = 0.3 s. Aceasta
eroare insa supraestimeaza eroarea si vom incerca acum sa calculam o eroare
medie:
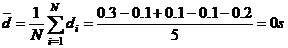
Vedem ca nu putem folosi media
deviatiilor pentru a estima eroarea deoarece obtinem zero: probabilitatea de a
obtine valori mai mari decat valoarea medie este egala cu probabilitatea de a
obtine valori mai mici decat valoarea medie si deviatiile cu semnul plus sunt
anulate de acelea cu semnul minus. Pentru a scapa de valorile negative vom
ridica deviatiile la puterea a doua, apoi vom calcula valoarea lor medie si vom
extrage radicalul din aceasta valoare obtinand formula deviatiei sau a abaterii standard:
 =
= 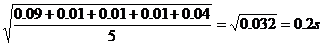
Acesta este rezultatul care ne
spune care este indepartarea medie a rezultatelor experimentale fata de
valoarea medie:
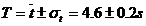
Definitia matematica exacta a
deviatiei sau abaterii standard este:
 .
.
Inlocuirea lui N cu N-1se
explica in urmatorul mod: in momentul cand calculam abaterea standard noi nu
cunoastem media adevarata, ci numai o estimare a ei la acel moment, 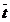 , ceea ce conduce la o subevaluare a abaterii standard.
Pentru a compensa diferenta, la valori mici ale lui N, vom imparti la N-1 in
loc de N.
, ceea ce conduce la o subevaluare a abaterii standard.
Pentru a compensa diferenta, la valori mici ale lui N, vom imparti la N-1 in
loc de N.
Patratul abaterii standard, 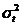 , se numeste varianta sau dispersie.
, se numeste varianta sau dispersie.
Pentru a fi mai siguri ca 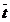 este o reprezentare exacta a valorii adevarate a marimii
masurate (perioada de oscilatie T), vom repeta setul de masurari de mai multe
ori. In acest caz definim deviatia sau abaterea standard a valorii
medii:
este o reprezentare exacta a valorii adevarate a marimii
masurate (perioada de oscilatie T), vom repeta setul de masurari de mai multe
ori. In acest caz definim deviatia sau abaterea standard a valorii
medii:  .
. 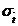 reprezinta o buna
estimare asupra incertitudinii asupra lui
reprezinta o buna
estimare asupra incertitudinii asupra lui 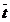 . Observam ca precizia masuratorilor creste de
. Observam ca precizia masuratorilor creste de 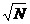 ori daca repetam masurarea de mai multe ori. Folosind datele
din exemplul de mai sus gasim
ori daca repetam masurarea de mai multe ori. Folosind datele
din exemplul de mai sus gasim  si rezultatul va fi:
si rezultatul va fi:
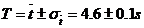 .
.
5.
Propagarea
erorilor
Sa presupunem ca avem o marime,
y, care depinde de mai multe variabile x1,, xn:
y = f (x1, x2, , xn) .
Daca presupunem ca erorile sunt
independente, abaterea standard a valorii medii a marimii y este data de
relatia:
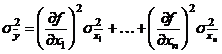 ,
,
numita teorema de propagare a erorilor.
6.
Histograme
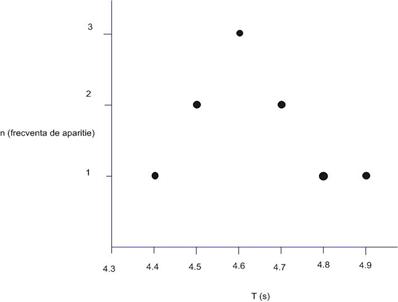
Sa presupunem ca am masurat
perioada pendulului de zece ori, obtinand urmatoarele rezultate: 4.9, 4.5, 4.7,
4.4, 4.5, 4.6, 4.7, 4.6, 4.8, 4.6 secunde.
Acum vom numara de cate ori am
obtinut fiecare rezultat:
|
Valorile
perioadei, T (s)
|
4.4
|
4.5
|
4.6
|
4.7
|
4.8
|
4.9
|
|
De
cate ori apar (frecventa de aparitie)
|
1
|
2
|
3
|
2
|
1
|
1
|
Putem reprezenta grafic
frecventa cu care apar valorile masurate ale perioadei:
Uneori este convenabil sa
folosim o histograma pentru reprezentare:
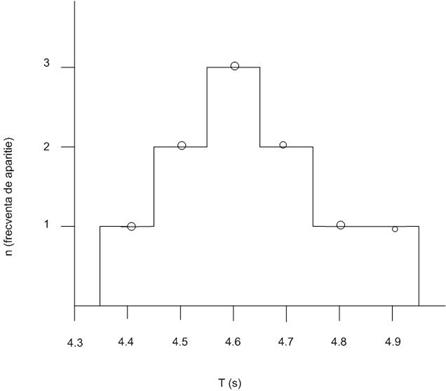
Cu cat numarul de masuratori
este mai mare, histograma se apropie din ce in ce mai mult de forma unui
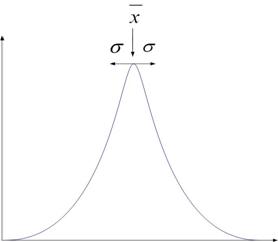
clopot, expresia grafica a functiei de distributie Gauss (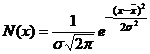 ):
):
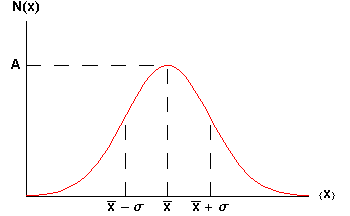
unde 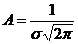 este amplitudinea
maxima,
este amplitudinea
maxima,  este valoarea medie, iar σ este deviatia standard a
distributiei.
este valoarea medie, iar σ este deviatia standard a
distributiei.
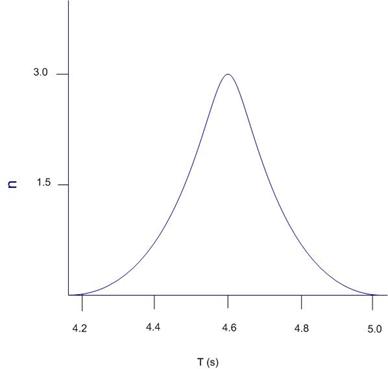
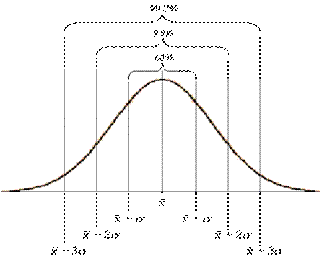
Care este relatia
dintre histograma si valoarea medie si eroarea cu care masuram perioada de
oscilatie a pendulului? De la inceput observam ca maximul histogramei este
situat chiar in dreptul valorii medii: 4.6 s. Daca vom calcula deviatia
standard cu formula anterioara, gasim valoarea: 0.14 s. Vom preciza intervalul
4.60 ± 0.14 pe histograma:
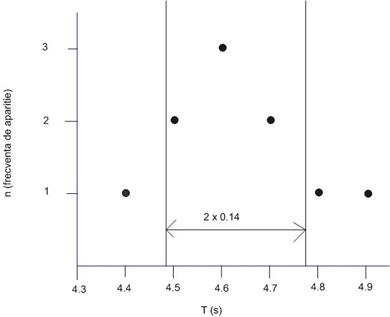
Observam ca valorile
4.5. 4.6 si 4.7 sunt cuprinse in intervalul definit de deviatia standard, ceea
ce inseamna ca 7 din 10 masuratori cad in acest interval. Se poate demonstra ca
distributia Gauss contine 68% din masuratori in intervalul definit de o
deviatie standard de fiecare parte a valorii medii. Deoarece histograma noastra
se apropie de distributia Gauss, am gasit in intervalul mentionat 70% din
masuratori, rezultat apropiat de valoarea teoretica de 68%. Pe baza celor discutate putem afla valoarea
medie si abaterea standard plecand de la o histograma data: gasim intai
valoarea centrala si apoi cautam largimea intervalului simetric de o parte si
de alta a ei in care sunt continute 68% (in practica 2/3) din masuratori.
Jumatate din acest interval va fi deviatia standard. In figura de mai jos aflam
ca avem o sansa de 68% ca valoarea adevarata a marimii masurate sa fie cuprinsa
in intervalul 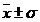 , o sansa de 95% ca valoarea adevarata a marimii masurate sa
fie cuprinsa in intervalul
, o sansa de 95% ca valoarea adevarata a marimii masurate sa
fie cuprinsa in intervalul 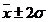 si o sansa de 99.7% ca
valoarea adevarata a marimii masurate sa fie cuprinsa in intervalul
si o sansa de 99.7% ca
valoarea adevarata a marimii masurate sa fie cuprinsa in intervalul 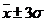 .
.
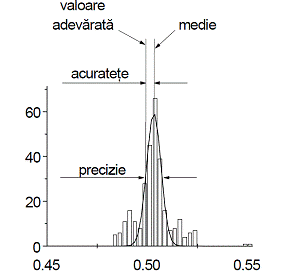
Acuratetea
indica indepartarea valorii obtinute prin masurare de valoarea adevarata a
marimii masurate. Astfel, daca folosim o
balanta si masurand o masa marcata de 50.0 g obtinem rezultatul 80.5 g,
masuratoarea facuta este lipsita de acuratete. Pentru a estima acuratetea, este
suficienta o singura masurare. Precizia
masoara imprastierea valorilor masurate fata de valoarea medie si este descrisa
cantitativ prin abaterea standard.
Figura urmatoare explica notiunile de acuratete si precizie:
7.
Distributia
normala (Gaussiana)
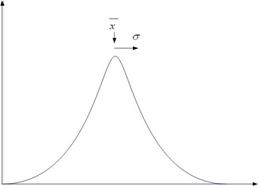
 este valoarea medie iar σ este abaterea sau deviatia
standard. Aproximativ 2/3 din masuratori sunt cuprinse in intervalul
este valoarea medie iar σ este abaterea sau deviatia
standard. Aproximativ 2/3 din masuratori sunt cuprinse in intervalul 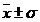 :
:
iar aproximativ 95% din
masuratori cad in intervalul 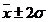 .
.
Multimea valorilor care se obtin
atunci cand efectuam masurari repetate asupra unei marumi fizice (de exemplu,
lungimea unui obiect) poarta numele de populatie
si, in exemplul ales, contine o infinitate de elemente. In practica se
efectueaza un numar finit de masuratori, multimea valorilor obtinute formand un
esantion. Media
aritmetica a populatiei se noteaza cu litera μ:
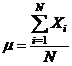 , in exemplul ales
, in exemplul ales  . Media aritmetica a
esantionului este:
. Media aritmetica a
esantionului este:
 unde, evident, n < N. Cu cat facem mai multe masuratori,
distanta dintre
unde, evident, n < N. Cu cat facem mai multe masuratori,
distanta dintre  si μ devine din
ce in ce mai mica:
si μ devine din
ce in ce mai mica:

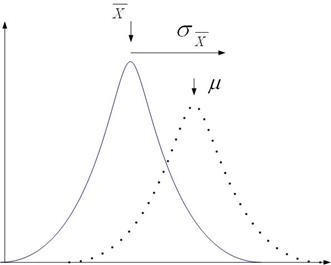
Deviatia
sau abaterea standard a valorii medii 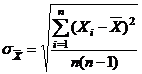 reprezinta
distanta fata de
reprezinta
distanta fata de  in interiorul careia ne asteptam sa gasim media aritmetica a
populatiei, μ. Cu o probabilitate de 68%, μ se va afla in intervalul
in interiorul careia ne asteptam sa gasim media aritmetica a
populatiei, μ. Cu o probabilitate de 68%, μ se va afla in intervalul  si cu o probabilitate
de 95%, μ se va afla in intervalul
si cu o probabilitate
de 95%, μ se va afla in intervalul  .
.
In concluzie, abaterea standard,
 masoara imprastierea
valorilor masurate intr-un esantion fata de valoarea medie a esantionului in
timp ce abaterea standard a valorii medii,
masoara imprastierea
valorilor masurate intr-un esantion fata de valoarea medie a esantionului in
timp ce abaterea standard a valorii medii, 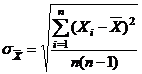 masoara
imprastierea valorilor medii obtinute in diferite esantioane fata de media
aritmetica a populatiei, μ. Marind numarul de masuratori, valoarea medie
si deviatia standard se vor modifica din ce in ce mai putin, in timp ce
deviatia standard a valorii medii se micsoreaza din ce in ce mai mult.
Imprecizia cu care masuram valoarea medie a unui esantion de valori are la baza
doua surse:
masoara
imprastierea valorilor medii obtinute in diferite esantioane fata de media
aritmetica a populatiei, μ. Marind numarul de masuratori, valoarea medie
si deviatia standard se vor modifica din ce in ce mai putin, in timp ce
deviatia standard a valorii medii se micsoreaza din ce in ce mai mult.
Imprecizia cu care masuram valoarea medie a unui esantion de valori are la baza
doua surse:
Eroarea masurarilor individuale;
aceasta este data de precizia aparatului de masura; cand nu cunoastem precizia
aparatului de masura, o vom considera ca fiind cel mai mic interval dintre
valorile masurate;
Abaterea standard a valorii
medii, considerata ca intervalul in jurul mediei pe esantion in care se afla cu
o mare probabilitate media asupra populatiei.
Eroarea
cu care masuram valoarea medie pe esantion va fi cea mai mare dintre cele doua:
eroarea masurarilor individuale si abaterea standard a valorii medii.
Din
cele discutate putem determina numarul optim de masuratori pentru determinarea
unei marimi fizice. El este acel numar pentru care precizia masurarilor
individuale devine egala cu abaterea standard a valorii medii:
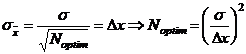
 ,
unde am notat cu Δx precizia masurarilor individuale.
,
unde am notat cu Δx precizia masurarilor individuale.

8.
Cifre
semnificative
Cifrele semnificative sunt
legate de procesul de "rotunjire" si implicit, de precizia rezultatului unei
masuratori. De exemplu, afirmatia ca lungimea unui caiet este de 20.143674217
cm nu are sens, deoarece nu dispunem de
un aparat de masura cu care sa masuram miliardimi de centimetru. In cazul
nostru, daca am masurat lungimea caietului cu o rigla gradata in milimetri,
rezultatul va fi 20.14 cm . In acest caz avem patru cifre semnificative: 2, 0,
1, si 4. De primele trei suntem siguri, iar ultima este o estimare grosiera a
zecimilor de milimetru, care poate fi eronata. Deci, cifrele semnificative ale
unei masurari sunt cele de care suntem siguri, plus ultima care poate fi estimata,
de care ne indoim si care contine eroarea. Prezentam cateva reguli de stabilire
a cifrelor semnificative:
Toate cifrele nenule se
considera semnificative: 231.67 are cinci cifre semnificative; in numarul 5000
prima cifra este semnificativa iar celelalte pot fi semnificative sau nu;
Zerourile care apar intre doua
cifre semnificative sunt cifre semnificative: 504.45 are cinci cifre
semnificative - 5, 0, 4, 4 si 5;
Zerourile din fata nu sunt
semnificative: 0.0024 are doua cifre semnificative - 2 si 4;
Zerourile din coada unui numar
zecimal cu virgula sunt semnificative: 24.500 are cinci cifre semnificative -
2, 4, 5, 0 si 0. Numarul 0.02400 are patru cifre semnificative - 2, 4, 0 si 0.
De asemenea 420.00 are cinci cifre semnificative - 4, 2, 0, 0 si 0.
Semnificatia zerourilor din
coada unui numar fara virgula zecimala este ambigua. De aceea exista diferite
conventii:  are trei cifre
semnificative, indicand o exactitate sau acuratete de ordinul zecilor;
are trei cifre
semnificative, indicand o exactitate sau acuratete de ordinul zecilor;  are doua cifre semnificative (cele care urmeaza dupa
are doua cifre semnificative (cele care urmeaza dupa 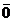 nemaifiind
semnificative; 3000. are patru cifre semnificative, indicate de prezenta
punctului zecimal.
nemaifiind
semnificative; 3000. are patru cifre semnificative, indicate de prezenta
punctului zecimal.
Cand folosim notatia stiintifica toate cifrele
sunt semnificative. De exemplu: 0.0023 cu doua cifre semnificative se scrie -
2.3 x 10-3, iar 0.003465200, cu sapte cifre semnificative se scrie -
3.465200 x 10-3. Pentru numerele fara virgula zecimala ambiguitatea
zerourilor din coada dispare: 26 000 cu cinci cifre semnificative se scrie:
2.6000 x 104 in timp ce 26 000 cu trei cifre semnificative se scrie
2.60 x 104.
In
calculele care implica inmultirea, impartirea, aplicarea unor functii
(trigonometrice, de exemplu) numarul de cifre semnificative ale rezultatului
trebuie sa fie egal cu cel mai mic numar de cifre semnificative ale numerelor
care sunt implicate in operatia matematica respectiva. Astfel daca evaluam ln (1.034 x 8.45) rezultatul trebuie sa
aiba trei cifre semnificative (1.034 are patru cifre semnificative iar 8.45 are
trei cifre semnificative): 2.167601217
va fi rotunjit pana la trei cifre semnificative : 2.17.
Daca
adunam sau scadem doua marimi, rezultatul trebuie sa aiba un numar de zecimale
(si nu de cifre semnificative) egal cu cel mai mic numar de zecimale ale
numerelor implicate in operatie matematica. Astfel daca adunam 23.14 cm cu 2.1
cm , primul numar are doua zecimale, iar al doilea are doar o zecimala.
Rezultatul adunarii, 25.24 cm, trebuie prezentat cu o singura zecimala: 25.2
cm. Cand avem de facut mai multe operatii matematice pentru a ajunge la
rezultatul final, trebuie ca in rezultatele intermediare sa pastram cu o cifra
semnificativa mai mult decat avem nevoie in rezultatul final, pentru a evita
erorile care apar prin rotunjire. Este gresit sa prezentam un rezultat cu mai
multe zecimale decat au datele experimentale, sau sa rotunjim la trei, sa
zicem, zecimale un rezultat intermediar si apoi sa prezentam rezultatul final
cu patru zecimale.
9.
Reprezentari grafice
Pentru a vedea cum depind una de
alta doua marimi fizice, este util sa facem o reprezentare grafica. Vom
modifica controlat una dintre variabile si vom inregistra valorile celeilalte
variabile, mentinand constanti ceilalti parametri. Valorile variabilei
controlate se reprezinta pe abscisa, iar valorile celeilalte variabile se
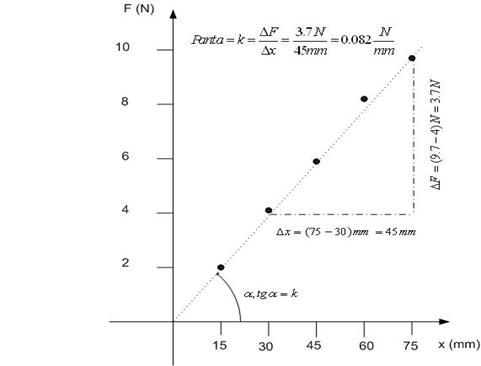
reprezinta pe ordonata. De exemplu, intr-un experiment studiem relatia dintre
forta deformatoare si deformarea unui resort elastic:
|
F (N)
|
2.0
|
4.1
|
5.9
|
8.2
|
9.7
|
|
x (mm)
|
15
|
30
|
45
|
60
|
75
|
Reprezentam pe
abscisa deformarea x a resortului si pe ordonata forta F deformatoare, care in
modul este egala cu forta elastica. Notarea marimii reprezentate pe axa este
obligatorie, ca si trecerea in paranteza a unitatii de masura a marimii
respective. Aceasta notare se face la mijlocul sau la capatul axei. Alegerea
lungimii unitatilor pe cele doua axe trebuie facuta cu grija pentru ca graficul
sa ocupe aproape tot spatiul graficului si nu sa fie concentrat intr-o fasie
ingusta a acestuia. Astfel, la capatul axei Ox trebuie sa avem valoarea maxima masurata
a variabilei x (75 mm), iar la capatul axei Oy trebuie sa avem o valoare
apropiata de forta maxima masurata (9.7 N), adica valoarea de 10 N.
Folosind metoda
celor mai mici patrate aflam parametrii dreaptei care minimizeaza suma
patratelor distantelor de la punctele experimentale la dreapta. Panta acestei
drepte ne ofera constanta k a resortului elastic (F = kx).



 =
=  .
. .
. 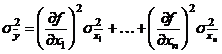 ,
,

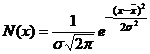 ):
): 






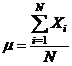 , in exemplul ales
, in exemplul ales  unde, evident, n < N. Cu cat facem mai multe masuratori,
distanta dintre
unde, evident, n < N. Cu cat facem mai multe masuratori,
distanta dintre 
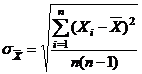
 masoara imprastierea
valorilor masurate intr-un esantion fata de valoarea medie a esantionului in
timp ce abaterea standard a valorii medii,
masoara imprastierea
valorilor masurate intr-un esantion fata de valoarea medie a esantionului in
timp ce abaterea standard a valorii medii,