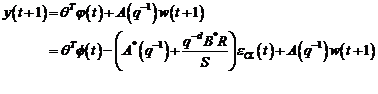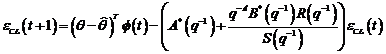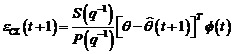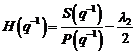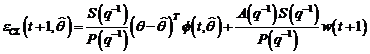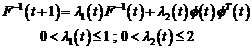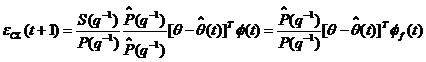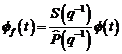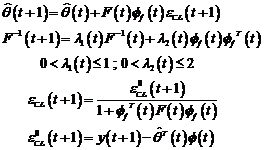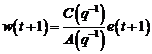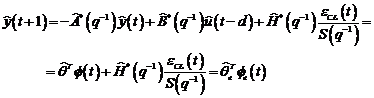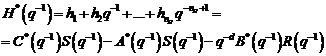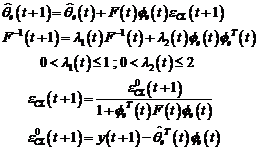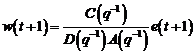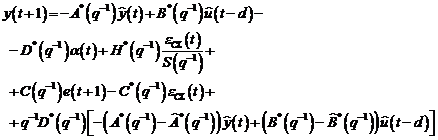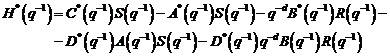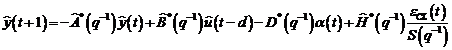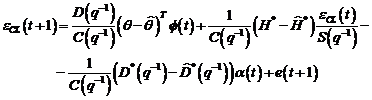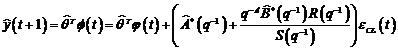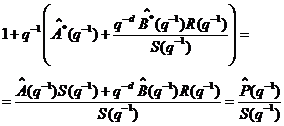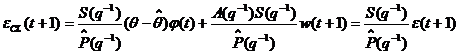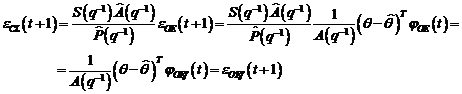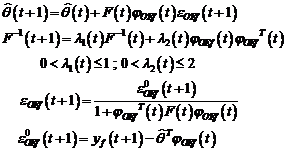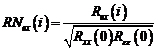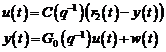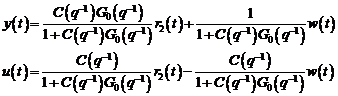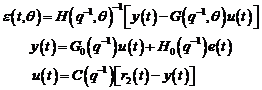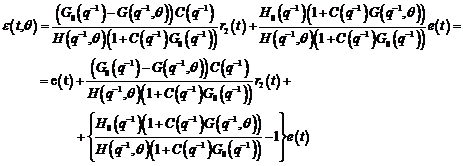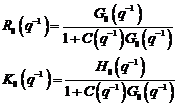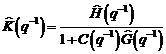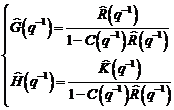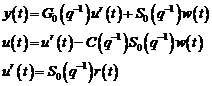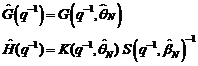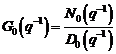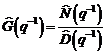Algoritmi
de identificare in bucla inchisa
In practica, exista multe situatii
in care identificarea in bucla deschisa este dificila sau imposibil de realizat
(de exemplu un proces cu un comportament integrator sau instabil in bucla
deschisa, etc.). Exista de asemenea sisteme automate in care procesul este cu
parametri variabili in timp, si prezenta unui regulator pentru pilotarea unui
astfel de proces este obligatorie. In acest caz se impune in mod evident
utilizarea identificarii in bucla inchisa pentru asemenea configuratii,
cunoscute ca sisteme adaptive de reglare.
Importanta practica a identificarii
in bucla inchisa este recunoscuta in literatura de specialitate si dovedita
prin aparitia si dezvoltarea unor metode specifice. Ideea centrala este de a
utiliza pe cat posibil, aceleasi tehnici de identificare folosite in bucla
deschisa (spre exemplu, algoritmii CMMPR),
in timpul exploatarii sistemului in bucla inchisa, cu precautii suplimentare.
Doua puncte de vedere pot fi evidentiate.
Primul, incearca reducerea problemei
identificarii in bucla inchisa la proceduri de tipul CMMPR pentru bucla deschisa din motive de ordin practic, algoritmii
si metodele de identificare in bucla deschisa fiind bine cunoscute si validate
la ora actuala. Acest punct de vedere a condus la aparitia metodelor CLOE (closed-loop output-error) care
utilizeaza in locul erorii de predictie 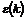 din algoritmul de adaptare CMMPR pentru ajustarea parametrilor
modelului de predictie, eroarea de iesire
din algoritmul de adaptare CMMPR pentru ajustarea parametrilor
modelului de predictie, eroarea de iesire 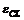 pentru
cazul sistemelor in bucla inchisa. Aceste metode furnizeaza estimari nedeviate
numai pentru anumite tipuri de perturbatie, luand in considerare faptul ca u si w sunt corelate.
pentru
cazul sistemelor in bucla inchisa. Aceste metode furnizeaza estimari nedeviate
numai pentru anumite tipuri de perturbatie, luand in considerare faptul ca u si w sunt corelate.
Al doilea punct de vedere, poate fi
considerat o extensie a primului si se bazeaza pe observatia conform careia,
intr-o configuratie de sistem in bucla inchisa, marimile u si w sunt corelate. Metodele dezvoltate au la baza aceeasi utilizare a
algoritmilor in bucla deschisa dar, in cateva scheme particulare, care permit o
decuplare virtuala a comenzii u de
perturbatia w. Aceste metode sunt
cunoscute sub denumirea de metode directe si metode indirecte de identificare
in bucla inchisa.
Vom trata cele doua abordari si vom
acorda o atentie mai mare primului caz, deoarece algoritmii cu care se opereaza
sunt prezentati in formula cunoscuta de la identificarea in bucla deschisa si
in consecinta sunt mai simplu de utilizat.
1
Algoritmi de identificare in bucla inchisa de tip eroare de predictie
Algoritmii prezentati in aceasta
sectiune functioneaza dupa principiul adaptarii parametrice, bazata pe eroarea
de predictie de la identificarea in bucla deschisa. Acesti algoritmi
prelucreaza in fapt eroarea de iesire, ca diferenta intre iesirea sistemului de
calcul cu modelul ajustabil inclus si iesirea sistemului fizic de reglare care
include procesul.
Schema de principiu pentru identificarea in bucla inchisa este prezentata
in figura 3.2. Scopul este de a minimiza eroarea intre cele doua sisteme,
obtinand estimari mai bune pentru noile modele care sunt utilizate eventual la
algoritmul de reglare.
In aceasta schema putem evidentia
doua tipuri de algoritmi de identificare in bucla inchisa.
- Primul tip scrie ecuatiile sistemului
in bucla inchisa avand la baza predictiile û(t), ŷ(t) si
valorile de eroare (de iesire)
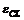 .
In aceasta maniera sunt generati: algoritmii recursivi de identificare in
bucla inchisa de tipul eroare de iesire, unde parametrii modelului (vezi
fig. 3.2) sunt ajustati prin algoritmul de adaptare parametrica AAP care utilizeaza eroarea
.
In aceasta maniera sunt generati: algoritmii recursivi de identificare in
bucla inchisa de tipul eroare de iesire, unde parametrii modelului (vezi
fig. 3.2) sunt ajustati prin algoritmul de adaptare parametrica AAP care utilizeaza eroarea 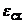 in locul erorii de predictie standard
in locul erorii de predictie standard 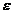
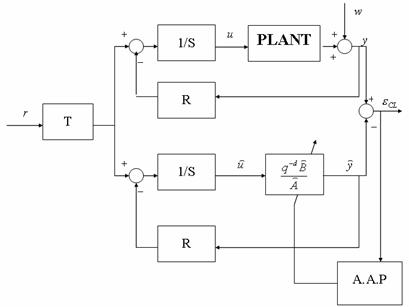
Fig.3.2: Schema
de identificare in bucla inchisa
- Cel de-al doilea tip scrie ecuatiile
predictorului utilizand marimile u(t),
y(t) si
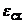 . Acest
fapt conduce la o exprimare a erorii de predictie utilizata de algoritmul CMMCR pentru identificarea in bucla
deschisa, calculata cu date filtrate. Aceasta clasa de algoritmi este
cunoscuta sub numele de algoritmi recursivi de identificare in bucla
inchisa cu date filtrate.
. Acest
fapt conduce la o exprimare a erorii de predictie utilizata de algoritmul CMMCR pentru identificarea in bucla
deschisa, calculata cu date filtrate. Aceasta clasa de algoritmi este
cunoscuta sub numele de algoritmi recursivi de identificare in bucla
inchisa cu date filtrate.
2
Relatii fundamentale pentru estimarea parametrilor
Scopul este de a estima parametrii
procesului dat de functia de transfer:
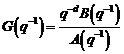 (3.63)
(3.63)
unde:
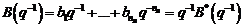 (3.64)
(3.64)
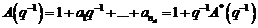 (3.65)
(3.65)
Iesirea sistemului in
bucla inchisa este data de:
 (3.66)
(3.66)
unde u(t) este intrarea procesului; y(t)
iesirea procesului; w(t) perturbatia,
si:
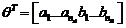 (3.67)
(3.67)
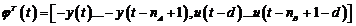 (3.68)
(3.68)
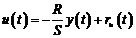 (3.69)
(3.69)
cu  semnal de excitatie externa aplicat
la iesirea regulatorului sau
semnal de excitatie externa aplicat
la iesirea regulatorului sau 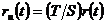 daca este aplicat la referinta.
daca este aplicat la referinta.
Ecuatia modelului de
predictie este:
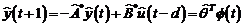 (3.70)
(3.70)
unde:
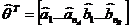 (3.71)
(3.71)
 (3.72)
(3.72)
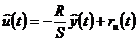 (3.73)
(3.73)
Eroarea de predictie este
definita sub forma urmatoare :
 (3.74)
(3.74)
Trebuie
retinut ca pentru valori constante ale parametrilor estimati, vectorul 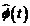 al modelului depinde numai de semnalele de excitatie externe. Deci, daca
presupunem ca r(t) (sau ru(t)) si perturbatia w(t) sunt independente, rezulta ca
al modelului depinde numai de semnalele de excitatie externe. Deci, daca
presupunem ca r(t) (sau ru(t)) si perturbatia w(t) sunt independente, rezulta ca 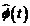 si
si 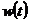 nu sunt corelate.
nu sunt corelate.
Pentru
toate metodele de identificare in bucla inchisa, algoritmul de adaptare
parametrica are aceeasi forma generala de exprimare:
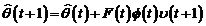 (3.75)
(3.75)
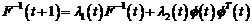 (3.76)
(3.76)
 (3.77)
(3.77)
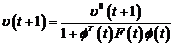 (3.78)
(3.78)
cu
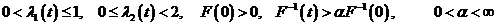
unde,
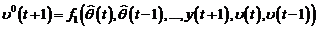
este o eroare de
adaptare a priori si:
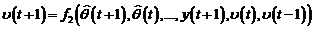
este o eroare de adaptare a posteriori.
Fiecare metoda de identificare in bucla deschisa va
utiliza reprezentarea generala pentru AAP,
cu expresii diferite pentru 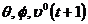 . Rolul secventelor
. Rolul secventelor  si
si  de ponderare este similar cu rolul
remarcat in cadrul prezentarii algoritmilor in bucla deschisa, adica de
definire a caracteristicilor de evolutie a amplificarii de adaptare F(t).
de ponderare este similar cu rolul
remarcat in cadrul prezentarii algoritmilor in bucla deschisa, adica de
definire a caracteristicilor de evolutie a amplificarii de adaptare F(t).
3 Algoritmi de tip eroare de
iesire
Pentru constructia
acestui tip de algoritm, se pleaca de la faptul ca iesirea sistemului in bucla
inchisa poate sa fie exprimata sub forma urmatoare:
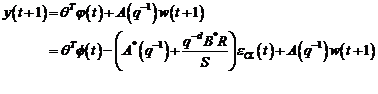 (3.79)
(3.79)
cu:
 (3.80)
(3.80)
unde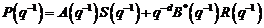 defineste polii sistemului in bucla inchisa.
defineste polii sistemului in bucla inchisa.
Din ecuatiile (3.70), (3.74), (3.79) pentru cazul
determinist, cu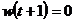 , avem:
, avem:
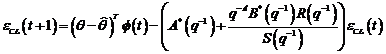 (3.81)
(3.81)
Dar, in conformitate cu
relatiile (3.80), (3.81) putem scrie:
 (3.82)
(3.82)
Algoritmul de adaptare
parametrica in versiune completa este dat de ecuatiile (3.75)-(3.78).
3.1 Algoritmul CLOE
Consideram in acest caz predictorul ajustabil a priori al
buclei inchise:
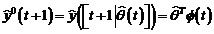 (3.83)
(3.83)
si predictorul a
posteriori dat de:
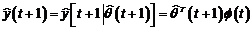 (3.84)
(3.84)
Definim eroarea de
predictie a priori :
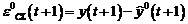 (3.85)
(3.85)
si cea a
posteriori :
 (3.86)
(3.86)
Rezulta expresia erorii
de predictie a posteriori :

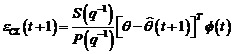 (3.87)
(3.87)
Algoritmul de adaptare
parametrica este dat de ecuatiile (3.75)-(3.78).
Avem conditiile
initiale :
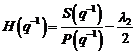 (3.88)
(3.88)
cu  , o functie reala, strict pozitiva. Algoritmul asigura o convergenta a
erorii de predictie la 0, in
absenta perturbatiilor.
, o functie reala, strict pozitiva. Algoritmul asigura o convergenta a
erorii de predictie la 0, in
absenta perturbatiilor.
Daca perturbatia exista,
ecuatia erorii de predictie, cu  cunoscut, este :
cunoscut, este :
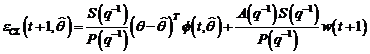 (3.89)
(3.89)
Daca presupunem ca w(t+1)
nu depinde de semnalul de excitatie externa 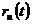 , rezulta ca
, rezulta ca  si
si 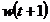 sunt independente. Daca avem o
intrare bogata in spectrul de frecventa, algoritmul asigura estimarea corecta a
parametrilor, respectand de asemenea conditia (3.88).
sunt independente. Daca avem o
intrare bogata in spectrul de frecventa, algoritmul asigura estimarea corecta a
parametrilor, respectand de asemenea conditia (3.88).
Algoritmul in acest caz
se scrie :
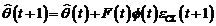
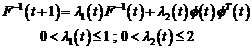
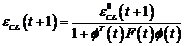
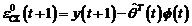
3.2 Algoritmul CLOE filtrat
Folosind expresia erorii de predictie din ecuatia (3.82), putem scrie
relatia :
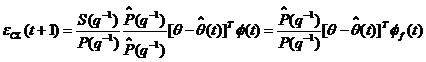 (3.90)
(3.90)
unde:
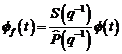 (3.91)
(3.91)
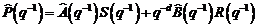 (3.92)
(3.92)
In ecuatia (3.92), 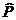 este polinomul caracteristic care aloca polii sistemului in bucla inchisa,
pe baza unei estimari initiale a modelului procesului (de exemplu prin
utilizarea unei metode de identificare in bucla deschisa).
este polinomul caracteristic care aloca polii sistemului in bucla inchisa,
pe baza unei estimari initiale a modelului procesului (de exemplu prin
utilizarea unei metode de identificare in bucla deschisa).
Aceasta formula ne conduce la algoritmul filtrat in bucla
inchisa de tip eroare de iesire, care utilizeaza conform procedurii AAP, setul de ecuatii (3.75)-(3.78):
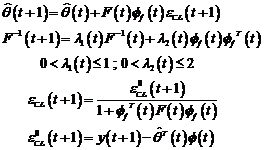 (3.93)
(3.93)
in care deci, eroarea de
iesire se calculeaza folosind date filtrate.
Convergenta algoritmului
este asigurata, in prezenta sau in absenta perturbatiilor si conditia (3.88)
este respectata.
Daca in algoritmul CLOE filtrat, inlocuim filtrul de date  cu
cu 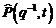 (estimarea polinomiala a buclei
inchise) obtinem algoritmul adaptativ
filtrat in bucla inchisa de tip eroare de iesire. Aceasta varianta asigura numai o
convergenta locala si un test de stabilitate trebuie sa fie aplicat
algoritmului.
(estimarea polinomiala a buclei
inchise) obtinem algoritmul adaptativ
filtrat in bucla inchisa de tip eroare de iesire. Aceasta varianta asigura numai o
convergenta locala si un test de stabilitate trebuie sa fie aplicat
algoritmului.
3.3 Algoritmul X-CLOE
Un algoritm de tipul X-CLOE
este folosit pentru cazul in care preturbatia este data de:
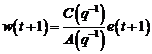
unde 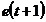 este un zgomot alb
gausian si
este un zgomot alb
gausian si 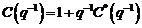 este un polinom
asimtotic stabil.
este un polinom
asimtotic stabil.
Modelul de predictie este
definit de:
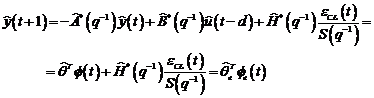 (3.94)
(3.94)
Iesirea procesului
devine:
 (3.95)
(3.95)
unde:
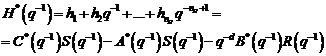 (3.96)
(3.96)
 (3.97)
(3.97)
Ecuatiile (3.94), (3.95) dau expresia erorii de
predictie:
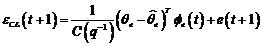 (3.98)
(3.98)
unde:
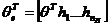 (3.99)
(3.99)
 (3.100)
(3.100)
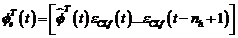 (3.101)
(3.101)
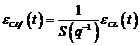 (3.102)
(3.102)
Din ecuatia (3.98), putem
sa observam ca, pentru 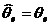 , eroarea de predictie tinde spre e(t+1).
, eroarea de predictie tinde spre e(t+1).
Prin inlocuirea predictorului fix al ecuatiei (3.94) cu
unul ajustabil, putem utiliza algoritmul de adaptare parametrica cu:
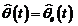
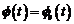
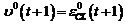
si obtinem :
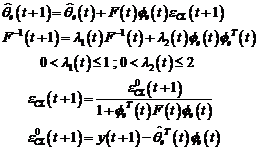 (3.103)
(3.103)
O analiza a functionarii algoritmului in absenta
perturbatiilor demonstreaza ca stabilitatea asimtotica globala este asigurata
fara sa fie obligatorie respectarea conditiei (3.88). In acest caz, expresia
erorii de predictie a posteriori este:
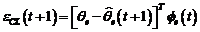 (3.104)
(3.104)
Daca perturbatiile exista,
eroarea de predictie a posteriori are expresia:
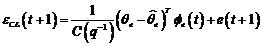 (3.105)
(3.105)
si algoritmul asigura o
estimare nedeviata a parametrilor, daca
se respecta conditia (3.88).
3.4 Algoritmul G-CLOE
Este utilizat in cazul in
care perturbatia se exprima sub forma:
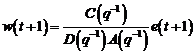
unde 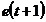 este un zgomot alb gausian, iar
este un zgomot alb gausian, iar 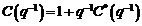 si
si 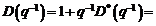 1+d1q-1+ . +dnDq-nD cu
1+d1q-1+ . +dnDq-nD cu  si
si  polinoame asimtotic
stabile.
polinoame asimtotic
stabile.
Ideea de constructie a acestui
tip de algoritm este similara cu aceea a algoritmului X-CLOE. Iesirea procesului in bucla inchisa este:
 (3.106)
(3.106)
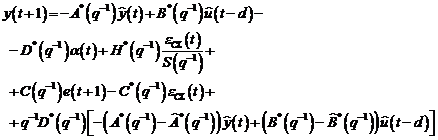 (3.107)
(3.107)
unde:
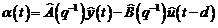 (3.108)
(3.108)
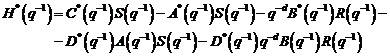 (3.109)
(3.109)
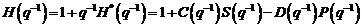 (3.110)
(3.110)
In aceste conditii,
modelul de predictie va avea forma:
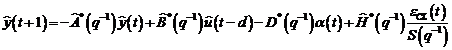 (3.111)
(3.111)
Expresia erorii de
predictie este obtinuta din ecuatiile (3.106) si (3.111).
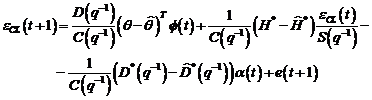 (3.112)
(3.112)
Ecuatia (3.112)
demonstreaza foarte clar ca pentru 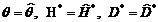 eroarea de predictie este egala cu
eroarea de predictie este egala cu 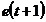
In absenta perturbatiilor, folosind
un predictor ajustabil in locul predictorului dat de ecuatia (3.111), eroarea
de predictie a posteriori are forma:
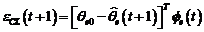 (3.113)
(3.113)
unde:
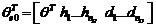 (3.114)
(3.114)
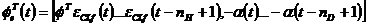 (3.115)
(3.115)
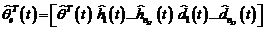 (3.116)
(3.116)
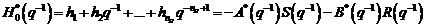 (3.117)
(3.117)
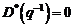 (3.118)
(3.118)
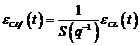 (3.119)
(3.119)
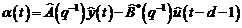 (3.120)
(3.120)
Algoritmul de adaptare
parametrica va folosi relatiile:
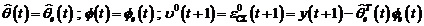
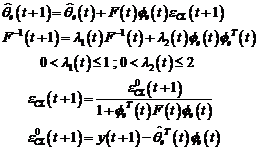
Acest algoritm asigura
convergenta erorii de predictie la 0.
In prezenta perturbatiilor, conditiile de convergenta nu
sunt cunoscute, din cauza expresiei pentru eroarea de predictie data de ecuatia
(3.112).
4 Algoritmi cu date filtrate
Posibilitatea utilizarii algoritmului de identificare in
bucla deschisa pentru identificarea in bucla inchisa este determinata de faptul
ca expresia predictorului, data de (3.70), poate sa fie scrisa si sub forma:

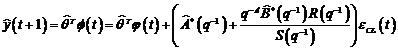 (3.121)
(3.121)
si mai departe,
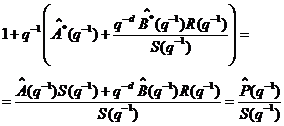
unde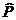 este polinomul caracteristic al sistemului in bucla inchisa, care aloca
polii in functie de modelul procesului.
este polinomul caracteristic al sistemului in bucla inchisa, care aloca
polii in functie de modelul procesului.
Prin utilizarea ecuatiilor (3.66) si (3.121) obtinem
expresia erorii de predictie:
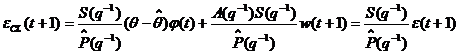 (3.123)
(3.123)
unde:
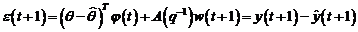 (3.124)
(3.124)
reprezinta eroarea de
predictie cand utilizam un predictor de tipul CMMPR pentru modelul procesului, definit astfel:
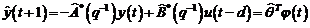 (3.125)
(3.125)
In consecinta, pentru estimarile cunoscute ale
parametrilor, eroarea de predictie in bucla inchisa este egala cu eroarea de
predictie din CMMPR, pentru iesirea
sistemului.
Ecuatia (3.123) poate sa
fie scrisa sub forma:
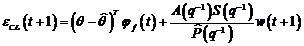 (3.126)
(3.126)
sau:
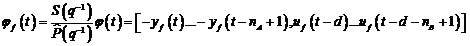 (3.127)
(3.127)
fiind posibila utilizarea
algoritmului CMMPR prezentat anterior
dar, pentru date de intrare si de iesire filtrate.
Filtrul utilizat are o caracteristica interesanta
deoarece asigura filtrarea semnalelor de frecventa inalta care depasesc
largimea de banda a modelului estimat al buclei inchise, iar daca regulatorul
contine un integrator (ex. 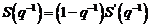 ) componentele continue vor fi de asemenea filtrate.
) componentele continue vor fi de asemenea filtrate.
Estimari nedeviate ale parametrilor modelului vor fi
obtinute numai pentru un anumit tip de zgomot si poli ai buclei inchise ( cum
ar fi spre exemplu cazul in care este indeplinita conditia ). Pentru observarea efectului zgomotului asupra estimarilor parametrilor,
putem utiliza alte metode recursive de identificare in bucla inchisa: metoda
Celor Mai Mici Patrate
Extinsa CMMPE, metoda Erorii de
Iesire cu Modelul de Predictie Extins EIMPE,
metoda Verosibilitatii Maxime VM.
). Pentru observarea efectului zgomotului asupra estimarilor parametrilor,
putem utiliza alte metode recursive de identificare in bucla inchisa: metoda
Celor Mai Mici Patrate
Extinsa CMMPE, metoda Erorii de
Iesire cu Modelul de Predictie Extins EIMPE,
metoda Verosibilitatii Maxime VM.
In
practica, aceste metode de identificare in varianta recursiva, pot fi utilizate
cu date de I/O filtrate prin filtrul 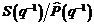 . In acest caz este necesara o estimare initiala a
modelului procesului pentru a putea implementa ulterior filtrul, lucru care nu
este utilizat pentru algoritmii de tip eroare de iesire
. In acest caz este necesara o estimare initiala a
modelului procesului pentru a putea implementa ulterior filtrul, lucru care nu
este utilizat pentru algoritmii de tip eroare de iesire
Algoritmii recursivi pentru identificare in bucla
deschisa pot deci sa fie utilizati pentru identificarea modelului procesului in
bucla inchisa si avem :
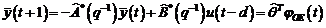 (3.128)
(3.128)
unde,
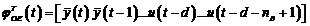 (3.129)
(3.129)
Ignorand efectul de
zgomot, eroarea de predictie obtinuta din ecuatiile (3.66), (3.129) este:
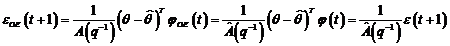 (3.130)
(3.130)
Deci:
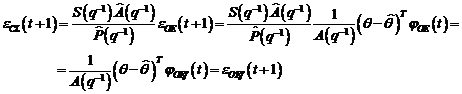 (3.131)
(3.131)
sau:
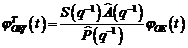 (3.132)
(3.132)
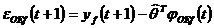 (3.133)
(3.133)
Algoritmul de adaptare
parametrica va fi urmatorul:
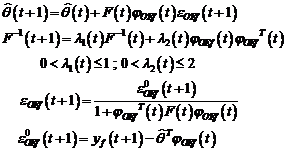 (3.134)
(3.134)
Este deci evident ca algoritmii de identificare in bucla
deschisa pot sa fie utilizati pentru identificarea in bucla inchisa cu datele
I/O filtrate de filtrul cu functia de sensibilitate 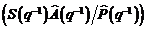 . Daca in bucla inchisa u si w sunt corelate, estimarile parametrilor
vor fi nedeviate numai pentru un anumit model de perturbatie si o anumita
alocare a polilor sistemului in bucla inchisa.
. Daca in bucla inchisa u si w sunt corelate, estimarile parametrilor
vor fi nedeviate numai pentru un anumit model de perturbatie si o anumita
alocare a polilor sistemului in bucla inchisa.
5 Validarea modelelor
Prima remarca pe care trebuie sa o facem este aceea ca
oricare criteriu sau test va fi folosit, validarea modelului depinde si de
regulator. Scopul validarii este de a descoperii modelul procesului care da o
predictie mai buna pentru procesul integrat in sistemul in bucla inchisa, deci
in prezenta regulatorului implicat in operatiunea de identificare.
Testul de validare statistica poate sa fie descris intr-o
maniera similara cu testul pentru identificarea in bucla deschisa, dar eroarea
de predictie este obtinuta cu ajutorul unui model de predictie al buclei
inchise.
Testul de
decorelare utilizeaza schema in care predictorul este dat de ecuatiile
(3.70)-(3.73), si decorelarea intre eroarea de predictie 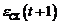 si componentele vectorului de
observatie
si componentele vectorului de
observatie  (
(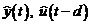 si valorile lor intarziate, va fi
stabilita prin calculul covariatiei valorii reziduale a erorii de
predictie.
si valorile lor intarziate, va fi
stabilita prin calculul covariatiei valorii reziduale a erorii de
predictie.
Exista doua motive care arata ca acest test este necesar:
pe de o parte, necorelarea intre vectorul observatiilor si eroarea de predictie
conduce la estimari nedeviate ale parametrilor, si pe de alta parte, din cauza
faptului ca acesta necorelare implica independenta intre eroarea de predictie
si excitatiile externe (eroarea de predictie reziduala nu contine informatii
care depind de semnalul de excitare extern, si pentru asta toate corelarile
intre semnalul de excitare si iesirea sistemului sunt descrise de predictor).
Definim:
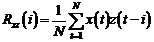 (3.135)
(3.135)
si calculam:
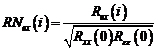

 (3.136)
(3.136)
Criteriul de validare
este:
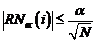 (3.137)
(3.137)
unde 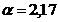 si N reprezinta numarul de date implicate in calcul functiei de
corelatie.
si N reprezinta numarul de date implicate in calcul functiei de
corelatie.
In multe situatii practice, folosind un singur set de
date putem obtine mai multe modele identificate, prin metode diferite. In acest
caz trebuie sa facem o validare comparativa, cu ajutorul indicatorilor 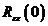 si
si 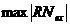 , calculati pentru fiecare model.
, calculati pentru fiecare model.
Testul de albire. Daca exista informatii
asupra efectului de zgomot alb asupra iesirii procesului, in mecanismul de
utilizare a algoritmului de identificare ales, trebuie sa facem un test de
albire asupra erorii de predictie reziduale.
Utilizam un predictor dat de ecuatia (3.94). Daca
cunoastem modelele de I/O ale
procesului si modelul de perturbatie, eroarea de predictie este zgomot alb.
Albirea erorii de
predictie implica:
a) obtinerea de estimari
nedeviate ale parametrilor;
b) modelul identificat
permite obtinerea predictorului optim pentru procesul in bucla inchisa;
c) decorelare intre eroarea
de predictie si semnalul de excitare extern.
Calculam:
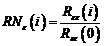
 (3.138)
(3.138)
Criteriul de
validare este dat de (3.137). Pentru validarea comparativa a mai multor modele,
indicatorii de performanta pentru test raman 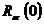 si
si 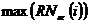
6 Metode directe si indirecte
de identificare in bucla inchisa
O alta abordare a
problemei de identificare in bucla inchisa, a fost propusa de Paul Van den Hof
si a generat categoria de metode directe si indirecte de identificare. Se considera sistemul in bucla
inchisa, dat in fig.3.3.

Figura 3.3: Structura de identificare
in bucla inchisa
Ecuatiile sistemului
sunt:
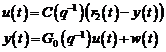 (3.139)
(3.139)
Rezulta cu usurinta
expresiile:
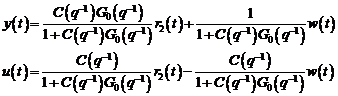 (3.140)
(3.140)
Folosind functia de
sensibilitate:
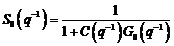 (3.141)
(3.141)
ecuatiile pot fi scrise
sub forma compacta:
 (3.142)
(3.142)
Luand ca punct de plecare aceste
ecuatii, avem doua metode de identificare in bucla inchisa:
a) Identificarea directa
utilizeaza perechea de date (u,y) si
identifica modelul ca si in cazul identificarii in bucla deschisa;
b) Identificarea indirecta,
estimeaza modelul sistemului in bucla inchisa si apoi utilizeaza modelul
cunoscut al regulatorului pentru calculul modelului procesului.
Pentru operatia de identificare
in bucla inchisa, aceste metode dispun de informatii despre:
comanda u(t)
si iesirea y(t);
resursele de caracterizare pentru semnalele 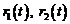
valorile marimilor masurate 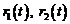 ;
;
structura regulatorului C (q-1).
Obiectivul procedurii de identificare in bucla inchisa, este determinarea
modelelor  si
si 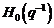
6.1
Tehnici directe de identificare
Metoda utilizeaza semnale masurate y(t), u(t) si identifica modelul
procesului fara sa faca apel la informatiile asupra regulatorului. O estimare parametrica poate sa fie
obtinuta prin minimizarea criteriului urmator:
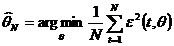 (3.143)
(3.143)
sau:
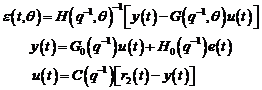 (3.144)
(3.144)
Daca combinam relatiile
de mai sus, deducem expresia:
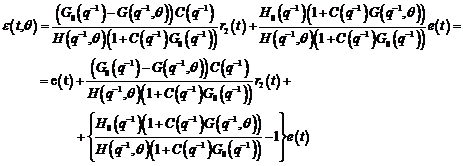
Metoda directa calculeaza
o estimatie consistenta daca,
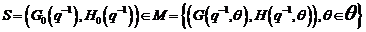
si sunt indeplinite
conditiile urmatoare:
a) semnalele
 sunt suficient de
persistente;
sunt suficient de
persistente;
b) C (q-1)
este un regulator de ordin suficient de mare;
c) C (q-1) este un regulator care comuta intre
anumite stari intre experimente (nelinear sau variabil in timp)
Identificarea directa poate sa
furnizeze estimari corecte pentru identificarea exacta a modelelor de tip ARMAX.
6.2. Tehnici de identificare
indirecte
Principala diferenta intre metodele indirecte si cele
directe, prezentate mai sus, este data de faptul ca metodele indirecte
utilizeaza un semnal exogen r1(t),
suficient de persistent pentru identificarea dinamicii procesului, avand in
vedere ca principalul obstacol de identificare in bucla inchisa este ca u(t) si w(t) sunt marimi corelate.
Sistemul in bucla inchisa
este prezentat in figura 3.4:
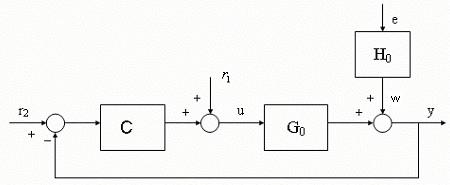
Figura 3.4: Sistemul in bucla inchisa
utilizat pentru identificare indirecta
Identificam modelul de la
intrarea r1(t) si iesirea y(t):
 (3.146)
(3.146)
sau:
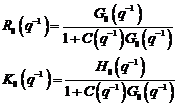 (3.147)
(3.147)
Construim sistemul in
bucla deschisa 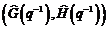 cu ecuatiile:
cu ecuatiile:
 (3.148)
(3.148)
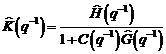 (3.149)
(3.149)
Folosind informatiile
despre regulatorul C(q-1),
calculam:
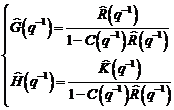 (3.150)
(3.150)
In aceasta maniera, folosind un semnal aplicat intre regulator si proces,
ajungem la o identificare de tip bucla deschisa, pentru ca intrarea si zgomotul
sunt necorelate, asigurand estimarea ansamblului 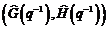
Doua metode utilizeaza
acest tip de identificare: metoda two-stages si metoda factorilor coprimi.
Algoritmul in doua etape
(two-stage)
Sistemul regulator + proces este cel din figura 4.4,
cu notatiile:

Ecuatiile sistemului, utilizate la aceasta abordare sunt:
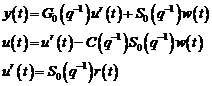 (3.151)
(3.151)
Aceasta metoda are doua etape:
Prima etapa:
a)
Se
cauta o conexiune in structura sistemului inchis pentru care intrarea este
necorelata cu zgomotul. Pentru aceasta, identificam ansamblul care asigura
transferul de la r la u:

Se ajunge in acest fel la o problema de identificare in bucla deschisa,
pentru care semnalul de proba este r(t)
si iesirea chiar semnalul de comanda u(t). Folosind una dintre metodele de
identificare in bucla deschisa, estimam functia de transfer intermediara 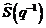
b) Utilizam estimarea lui 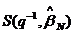 pentru calculul
semnalului intermediar, semnal de tipul "zgomot alb":
pentru calculul
semnalului intermediar, semnal de tipul "zgomot alb":

A doua etapa:
Calculam modelul procesului 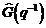 prin identificarea transferului intre
prin identificarea transferului intre 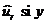 , folosind
eroarea de predictie:
, folosind
eroarea de predictie:
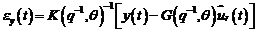
Estimarea  este folosita numai pentru generarea
semnalului
este folosita numai pentru generarea
semnalului 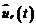 si modelului procesului este determinat in a
doua etapa. Modelul rezultat este obtinut prin:
si modelului procesului este determinat in a
doua etapa. Modelul rezultat este obtinut prin:
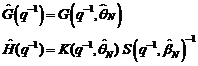 (3.152)
(3.152)
Algoritmul in doua
etape este utilizat cand marimile u
si e sunt corelate, respectiv, cand C(q-1) nu este cunoscut cu
exactitate.
Algoritmul factorilor comprimi
Folosind
schema din figura 4.4, unde sistemul este descris prin ecuatiile:
 (3.153)
(3.153)
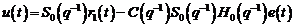 (3.154)
(3.154)
notam:
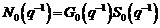
 (3.155)
(3.155)
rezulta:
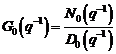 (3.156)
(3.156)
Factorizarea este comprima daca factorii sunt stabili,
respectiv sistemul  nu prezinta zerouri instabile.
nu prezinta zerouri instabile.
 pot sa fie estimate prin utilizarea
metodelor de identificare in bucla deschisa cu apelarea marimilor
pot sa fie estimate prin utilizarea
metodelor de identificare in bucla deschisa cu apelarea marimilor 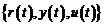 si avem:
si avem:
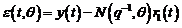 (3.157)
(3.157)
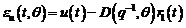 (3.158)
(3.158)
Obtinem in continuare,
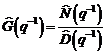 (3.159)
(3.159)
Acest tip de identificare
in bucla inchisa permite accesul la factorii procesului prin utilizarea
semnalelor exogene 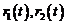 si al transferului intre
si al transferului intre 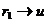 , respectiv
, respectiv 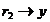 . Identificarea acestor factori poate sa fie facuta cu ajutorul metodelor
de identificare in bucla deschisa. Semnalul
. Identificarea acestor factori poate sa fie facuta cu ajutorul metodelor
de identificare in bucla deschisa. Semnalul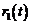 poate fi usor calculat daca se cunoaste regulatorul C(q-1) ,cu relatia:
poate fi usor calculat daca se cunoaste regulatorul C(q-1) ,cu relatia:
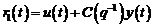 (3.160)
(3.160)
Cele mai performante
dintre metodele prezentate pentru identificare in bucla deschisa si inchisa
sunt implementate sub forma unor produse software dedicate sau integrate in
alte produse standard, existente pe piata, de larga utilizare in teoria
sistemelor.
Bibliografie:
[1] Eykhoff
P., System Identification: Parameter
and State Estimation, John Wiley, London,
1974.
[2] Goodwin
G. C., Payene R. L., Dynamic System Identification: Experiment design and Data Analysis, Academic
Press, New-York, 1977.
[3] Ljung
L., Soderstroom T., Theory and
Practice of Recursive Identification, MIT Press, Cambridge,Massashusetts, 1983.
[4] Soderstroom
T., Stoica P., System Identification,
Prentice Hall, New-York, 1989.
[5] Landau
I. D., Identification et Commande des
Systemes, Hermes, Paris, 1995.
[6] Van
den Hof P., Identification in Closed
Loop, Ecole d'Ete, Grenoble,
1998.
[7] Bitmead B.,
Identification for Control, Ecole
d'Ete, Grenoble,
1998.



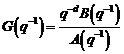
 (3.77)
(3.77)