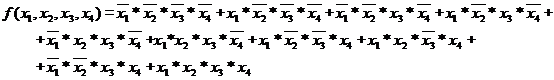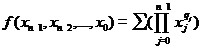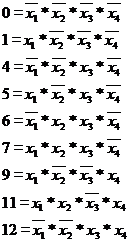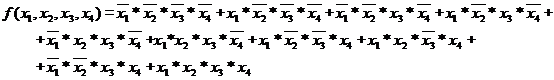Minimizarea
functiilor logice
Prin minimizarea functiilor
logice se intelege procesul de simplificare a expresiei algebrice a unei
functii prin reducerea numarului de termeni si/sau a
numarului de variabile de intrare care intra in componenta
functiei. Problema minimizarii este legata de conditiile
cele mai avantajoase ale realizarii unui circuit fizic care sa
realizeze functia logica respectiva. In aceste conditii,
operatia de minimizare este insotita de unele aspecte de ordin
tehnologic cum ar fi:
- utilizarea unui numar cat mai
mic de elemente de circuit;
- obtinerea unui numar minim
de blocuri componente in schema;
- obtinerea unui cost minim;
- realizarea unei scheme logice care
sa permita o depanare usoara;
- rezolvarea problemelor de hazard
care duc la functionarea eronata a schemei;
Vom numi disjunctie
elementara a unor variabile, suma logica a acestora sau a
complementelor lor.
Formula generala pentru acest
tip de forma canonica este urmatoarea:
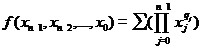
Pentru a ajunge la forma
canonica disjunctiva a unei functii logice oarecare trebuie
parcurse urmatoarele etape:
Se scrie tabelul de adevar al
functiei logice respective;
Din tabelul de adevar se vor
considera toate combinatiile variabilelor de intrare pentru care
functia are valoarea 1;
Pentru fiecare din aceste
combinatii se scriu termenii canonici conjunctivi astfel: fiecare termen
canonic conjunctiv e format din produsul logic al tuturor variabilelor de
intrare nenegate sau negate dupa cum in combinatia respectiva
variabila binara are valoarea 1 sau 0;
Toti termenii canonici
conjunctivi se reunesc sub operatia de produs logic.
Exemplu:
Consideram functia: f =
R(2, 3, 8, 10, 13, 14)
1) Tabelul de adevar este
urmatorul:
2) Consideram variabilele de
intrare pentru care functia are valoarea 0:
i = 0, 1, 4, 5, 6, 7, 9, 11, 12, 15
Se scriu termenii canonici
conjunctivi:
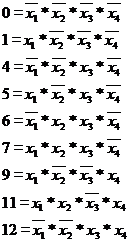
13 = x1 * x2 * x3 * x4
4)Forma canonica
disjunctiva a functiei este urmatoarea: