|
Ce este o aplicatie
liniara?
|
Fie V si W doua spatii vectoriale peste acelasi
corp K. Aplicatia f: V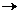 W se numeste W se numeste
aplicatie liniara sau morfism de K-spatii vectoriale daca sunt indeplinite conditiile:
f(x+y)=f(x)+f(y), 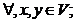
f(ax)=af(x), 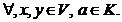
Observatia
1 1) Avem ca f(0V)=0W si f(-x)=-f(x).
2. f este
aplicatie liniara daca si numai daca f(ax+by)=af(x)+bf(y), 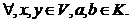
Observatia 2. Daca f: V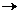 W, este o aplicatie liniara si B1=,
B2=sunt baze
in spatiile vectoriale V, respectiv W, atunci exista o unica
matrice A=(aij)i, W, este o aplicatie liniara si B1=,
B2=sunt baze
in spatiile vectoriale V, respectiv W, atunci exista o unica
matrice A=(aij)i,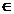 ,j ,j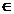 , unde n=dimV si m=dimW astfel incat f(ei)= , unde n=dimV si m=dimW astfel incat f(ei)= Daca elementul x Daca elementul x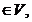 x= x=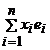 , atunci elementul y=f(x)= , atunci elementul y=f(x)= 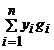 are coordonatele yi= are coordonatele yi= Ultima relatie se mai poate scrie Y=AX. Matricea A se numeste matricea
asociata aplicatiei liniare f
in raport cu bazele B1, B2. Ultima relatie se mai poate scrie Y=AX. Matricea A se numeste matricea
asociata aplicatiei liniare f
in raport cu bazele B1, B2.
|
|

|
Test de
autoevaluare 2.1.
- Sa se verifice care dintre urmatoarele aplicatii
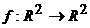 sunt liniare: sunt liniare:
a) f(x1,
x2)=(x1, x1x2);
b) f(x1,
x2)=(2, x1+x2);
c) f(x1,
x2)=(2x1+4x2, x1-2x2);
2.
Aratati ca functia 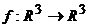 , f(x)= (2x1+4x2-3x3,
x1-2x2+x3, 5x1+7x2+x3)
este aplicatie liniara si scrieti matricea asociata ei in baza
canonica. , f(x)= (2x1+4x2-3x3,
x1-2x2+x3, 5x1+7x2+x3)
este aplicatie liniara si scrieti matricea asociata ei in baza
canonica.

Raspunsul se va da in spatiul gol de mai sus.
Raspunsul la test se gaseste la pagina xx.
|


 Daca elementul x
Daca elementul x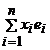 , atunci elementul y=f(x)=
, atunci elementul y=f(x)= 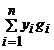 are coordonatele yi=
are coordonatele yi= Ultima relatie se mai poate scrie Y=AX. Matricea A se numeste matricea
asociata aplicatiei liniare f
in raport cu bazele B1, B2.
Ultima relatie se mai poate scrie Y=AX. Matricea A se numeste matricea
asociata aplicatiei liniare f
in raport cu bazele B1, B2.