

 yB B
yB B
YA A
xA xB
O
Vectorul 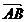 are cooordonatele xB- xA (abscisa ) si yB- yA (ordonata )
are cooordonatele xB- xA (abscisa ) si yB- yA (ordonata )
Raportul 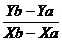 =m este panta
dreptei AB
=m este panta
dreptei AB
Considerand vectorii  (x,y) si
(x,y) si 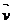 (x',y').Afirmatia ,,
(x',y').Afirmatia ,, este coliniar
cu
este coliniar
cu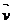 ,, se traduce
vectorian ,, k un numar real nenul astfel incat
,, se traduce
vectorian ,, k un numar real nenul astfel incat  =k
=k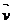 ,, este ceea ce
imseamna,din punct de vedere al coordonatelor,x=kx' si y=ky',adica
proportionalitatea coordonatelor.
,, este ceea ce
imseamna,din punct de vedere al coordonatelor,x=kx' si y=ky',adica
proportionalitatea coordonatelor.
Retinem deci : (x,y) si
(x,y) si 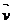 (x',y') sunt coliniari
(x',y') sunt coliniari 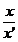 =
=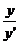 =k,x',y'
=k,x',y'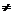 0
0
Sau  (x,y) si
(x,y) si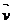 (x',y') sau coliniari xy'-x'y=0
(x',y') sau coliniari xy'-x'y=0
Teorema ecuatia
dreptei d determinata de punctul M(xm,ym) si de vectorul director  (a b) este :y-yM=
(a b) este :y-yM=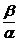 (x-xM)
(x-xM)
Dreapta
determinata de doua puncte
Fie A(xA,yA)
si B(xB,yB)doua puncte ;ele determina in mod unic
dreapta AB.A gasi ecuatia dreptei determinata de punctele A,B revine la a gasi
ecuatia dreptei data de punctul A(xA,yA)si de vectorul director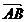 (xB-xA,yB-yA)
(xB-xA,yB-yA)
OBS. FieA(xA-yA),B(xB,yB)
doua puncte;dreaptaABare ecuatia
y-yA=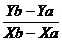 (x-x1)
(x-x1)
Sa observam ca
panta dreptei AB este m=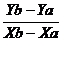
Sa determinam
ecuatia dreptei AB,A(-3,1),B(0,4)
Panta dreptei
este m=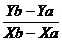 =
= =1 si ecuatia este y-yA=m(x-xA) ;y-1=1*(x-(-3)) ;y-1=x+3,deci
y=x+4
=1 si ecuatia este y-yA=m(x-xA) ;y-1=1*(x-(-3)) ;y-1=x+3,deci
y=x+4
 Y
Y






 B
B
yB
A
yA
0 xA xB X
Dreptele
distincte de ecuatie y=mx+n si y=m'x+n' sunt paralele daca si numai daca m=m'.
Ecuatia
dreptei determinata de doua puncte
Doua puncte
distincte M1(x1,y1),M2(x2,y2)determina
o dreapta unica d.
Daca x1=x2,atunci
dreapta d este verticala si are ecuatia x=x1.Daca y1=y2,atunci
dreapta d este orizontala si are ecuatia y=y1.Daca x1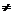 x2, atunci dreapta d este oblica.
x2, atunci dreapta d este oblica.



 Y
Y
 y=y1
y=y1
x=x1
 x
x
0 x
Ecuatia
carteziana a dreptei oblice d este determinata de punctul M1(x1,y1)de
panta m=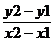 .Astfel,d :y-y1=
.Astfel,d :y-y1=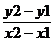 (x-x1)
(x-x1)
Daca (x2-x1)(y2-y1)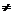 0(adica dreapta nu este orizontala si nici verticala),atunci
ecutia d se scrie eshivalent sub forma :
0(adica dreapta nu este orizontala si nici verticala),atunci
ecutia d se scrie eshivalent sub forma :
 =
=
Conditia de
coliniaritate a trei puncteMi(xi,yi),i=1,2,3
se scrie :

 x1 y1 1
x1 y1 1
x2 y2 1 =0
x3 y3 1
EX.Se dau
punctele A -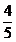 ,2 B(
,2 B( , ),c(1,5).Sa se gaseasca
ecuatia dreptei AB si sa se verifice ca punctele A,B,C sunt coliniare.
, ),c(1,5).Sa se gaseasca
ecuatia dreptei AB si sa se verifice ca punctele A,B,C sunt coliniare.
Dreapta
AB are ecuatiaadica  =
=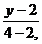 ,adica
,adica =
=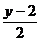 .Deoarece
.Deoarece  punctul C se afla pe dreapta AB ,adica punctele A,B,C sunt
coliniare.
punctul C se afla pe dreapta AB ,adica punctele A,B,C sunt
coliniare.
Ecuatia
dreptei oblice determinata de un punct si de o panta
O dreapta oblica
d este determinata printr-un punct MO(x0,y0)Id si prin panta m (care da directia dreptei)Ce conditie trebuie sa verifice
x si y pentru ca punctul M(x,y) sa fie situat pe dreapta d ?
OBS.Fie dreapta d
definita prin punctul M0(x0,y0)I d si prinh panta m.
Punctul
M(x,y)apartine dreptei d si daca si numai daca y-y 0=m(x-x0).
Demonstratie :Evident,M0(x0-y0)Id satisface relatia din teorema.De asemenea punctul M(x,y) M0(x0,y0) apartine dreptei d
daca si numai daca panta data este egala cu panta
calculata(fig.I.13),adica m=
M0(x0,y0) apartine dreptei d
daca si numai daca panta data este egala cu panta
calculata(fig.I.13),adica m= ,x
,x x0.
x0.
Afirmatia,,dreapta
d este multimea punctelor M(x,y) cu proprietatea (x,y)IR2 si y-y0=m(x-x0)''este
prescurtata prin d :y-y0=m(x-x0)
Aceasta ecuatie
edte de forma y=mx+n,undem este panta,iar n=y0-mx0.
Numarul real n se
numeste ordonata la origine,deoarece dreapta d intersecteaza Oy in punctul(O,n)
In particular,ecuatia
dreptei oblice care trece pri origine,x0=0,y0=0,si are
panta m este y=mx.Pentru m=1 obtinem y=x care este ecuatia primei bisectoare a
unghiurilor axelor de coordonate,iar pentru m=-1 gasim y=-x,care este ecuatia
celei de a doua bisectoare a unghiurilor axelor de coordonate(fig.I.14)

 y
y
y

 y=x y=x
y=x y=x
M(x,y)
 x
x
M0(x0,y0) 0
x
0 m= ,x
,x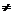 x0
x0
fig.I.13 fig.I.14
EX.Se da triunghiul de vf A(-1,3),B(2,-1),C(3,6).
Sa se gaseasca :1)ecuatia
dreptei AC
2)ecuatia
paralelei prin B la AC
3)ecuatia mediatoarei segmentului[BC]
1)Panta dreptei
AC este m=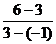 =
= .Aceasta panta si punctul A(-1,3) fixeaza ecuatia y-3=
.Aceasta panta si punctul A(-1,3) fixeaza ecuatia y-3= (x+1) sau,in forma carteziana explicita,y=
(x+1) sau,in forma carteziana explicita,y= x+
x+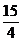
2)Orice paralela
la AC are panta m= .De aceea paralela prin B la AC are ecuatia y+1=
.De aceea paralela prin B la AC are ecuatia y+1= (x-2) sau explicit y=
(x-2) sau explicit y= x-
x-
3)Mijlocul M al
segmentului BC are coordonatele  .Panta dreptei BC este mBC=
.Panta dreptei BC este mBC= =7.Mediatoarea
segmentului BC este dreapta perpendiculara pe BC ce trece prin mijlocul
M.Astfel,mediatoarea are panta m=-
=7.Mediatoarea
segmentului BC este dreapta perpendiculara pe BC ce trece prin mijlocul
M.Astfel,mediatoarea are panta m=- =-
=- si are
ecuatia y-
si are
ecuatia y-
Coordonate carteziene in plan
Fie un plan P si d o dreapta oarecare din planul P.Fie O,AId doua punte distincte si R multimea numerelor reale.Prin axioma riglei
admitem ca exista o functie bijectiva
f:d R,f(M)=x.Prin axioma riglei admitem ca exista o funtie bijectiva f:d R,f(M)=x,care indeplineste urmatoarele
conditii:
1)f(O)=O,f(A)>0;
2)PQ= f(Q)-f(P) P,QId,
unde PQ este distanta dintre punctele P si Q.O asemenea functie se numeste
sistem de coordonate pe dreapta d,iar dreapta d pe care s-a fixat un sistem de
coordonate se numeste axa de coordonate.Punctul O se numeste originea
sistemului de coordonate,iar sensul de la O la A pe axa se numeste sens
pozitiv.Numarul real x se numeste adcisa sau coordonata punctului M in sistemul
de cordonate considerat.
Prin traditie,in loc de f(M)=x se scrie M(x) si se citeste ,,punctul M de
abcisa
 (coordonata)x'' sau ,,M de x'',iar sensul
pozitiv pae axa se marcheaza printr-o sageata.Axa de coordonate se deseneaza ca
in fig I.1 si se noteaza cu Ox.Punctul I de abcisa se numeste punct unitate.
(coordonata)x'' sau ,,M de x'',iar sensul
pozitiv pae axa se marcheaza printr-o sageata.Axa de coordonate se deseneaza ca
in fig I.1 si se noteaza cu Ox.Punctul I de abcisa se numeste punct unitate.




 Fig.I.1
Fig.I.1
M'(-x) I'(-1) O(o) I(1) M(x) x
Fie (Ox,Oy) o pereche ordonata de axe
ortogonale in planul P,cu originea O comuna si cu sensurile pozitive ale axelor
indicate prin sageti ca in fig I.2.Acest ansamblu poarta numele de reper
cartezian in planul P si se noteaza cu xOy.Punctul O se numeste originea
reperului.
y
0 x
fig.I.2
Punctele unitate I pe Ox si J pe Oy(OI=OJ) impun scara desenelor.Evident,aceste
puncte nu trebuie sa fie neaparat normalizate in desen.9fig.I.3)
Fie M un punct din planul P in care s-a fixat un reper cartezian
xOy.Paralela prin M la axa Oy intalneste axa Ox in punctul P,iar paralela prn M
la axa Ox intalneste axa Oy in punctul Q .Fie x coordonata lui P pe axa O x si
y coordonata lui Q pe axa Oy.in acest
fel punctului M(fig.I.3)I se ataseaza o pereche ordonata unica de numere
reale(x,y).Functia f:P R2,f(M)=(x,y) este bijectiva si
se numeste sistem de coordonate cartezian definit de reperul xOy pe planul
P.Prin traditie,in loc de f(M)=(X,Y) se scrie M (x,y) si se citeste,,punctul M
de abcisa x si ordonata y'' sau,,punctul M de coordonate carteziene x si y'' sau ,,M de x si y''.

 y y
y y



 P(o,y) M(x,y) y=y0
P(o,y) M(x,y) y=y0
y x=x0
 x x
x x
x P(x,o) 0



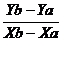

 =
= punctul C se afla pe dreapta AB ,adica punctele A,B,C sunt
coliniare.
punctul C se afla pe dreapta AB ,adica punctele A,B,C sunt
coliniare.