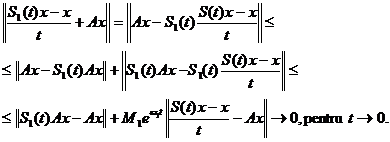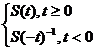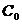Semigrupuri. Definitie . Proprietati.

- semigrupuri. Definitie . Proprietati

In acest paragraf introducem notiunea de semigrup de operatori liniari, prezentam proprietatile fundamentale ale acestuia, precum si exemple de semigrupuri de operatori liniari in spatii Banach.

Fie X un spatiu Banach real sau complex. In tot ceea ce urmeaza, notam cu B(X) algebra Banach a operatorilor liniari si marginiti pe X .

Definitia I.1.1. O familie S = 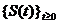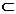B(x) se zice semigrup de operatori daca indeplineste urmatoarele conditii:

(i) S(0) = I , identitatea pe spatiul X;

(ii) S(t+s) = S(t)S(s), pentru orice t , s 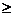0.

Daca in plus, are loc

(iii) 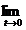S(t)x = x, pentru orice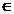 x X

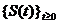
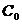atunci S = se zice de clasa sau 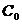- semigrup.

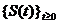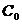Fie S = un - semigrup pe X . Consideram multimea

D(A) : = .

Remarca I.1.1. D(A) este un subspatiu liniar in X.

Definitia I.1.2. Operatorul

A : D(A)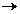 X, Ax : =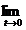

se numeste generatorul infinitezimal al 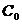- semigrupului S = .

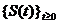Vom prezenta acum doua exemple importante de 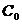- semigrupuri.

Exemplul I.1.1. Fie A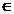B(X) si pentru fiecare t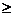0, fie

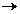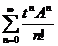S(t) : XX, S(t)x : =x.

Observam ca S(0) = I , iar pentru t,s 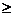0 avem succesiv:

S(t)S(s) = =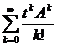

==

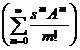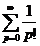
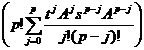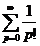
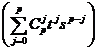
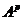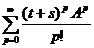= = = S(t+s).

In plus, avem ca

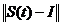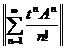
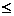
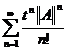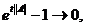= = pentru t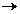0.

Din cele de mai sus, deducem ca S = 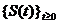este un 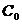- semigrup.

Uzual acesta se noteaza cu si X = 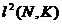: = 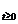, respectiv S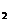= 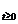, atunci

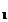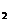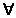S(t)= S(t) , t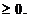

Demonstrație : Fie x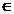 D(A) și t>0. Definim

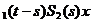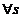
u(s)= S , 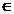[0,t].

Din Teorema I.1.2. rezulta ca

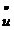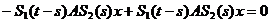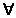(s)= , s.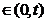

Inseamna ca u este constanta . In particular , u(0)=u(t), deci

S,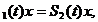

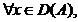
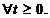
Din proprietatea de densitate a domeniului generatorului , obținem in final ca

S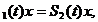

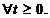
Definiția I.1.3. O familie U=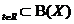se zice 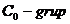daca indeplinește urmatoarele condiții :

(i) U(0) = I , identitatea pe spațiul X;

(ii) U(t+s)= U(t)U(s), pentru orice t,s ;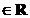

(iii) 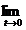U(t)x=x , pentru orice x ;

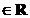In mod analog cu cazul semigrupurilor , pentru un C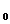- grup introducem mulțimea

D(A):.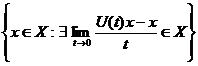

Remarca I.1.2. D(A) este un subspațiu liniar in X.

Definiția I.1.4. Operatorul

A : D(A) 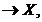Ax:=

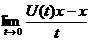
se numește generatorul infinitezimal al 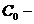grupului U = .

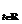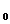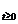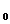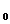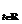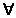Definiția I.1.5. Spunem ca un C- semigrup S= poate fi extins la un C- grup daca exista un C- grup U= astfel incat U(t)=S(t) , t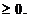

Problema : In ce condiții un C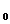- semigrup poate fi extins la un C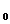- grup?

In continuare, vom raspunde problemei de mai sus. Pentru inceput, demonstram :

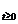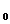Teorema I.1.3. Fie S= un C- semigrup pe X, iar A generatorul sau infinitezimal. Daca pentru fiecare t>0, S(t) este inversabil , atunci

S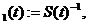 t>0

formeaza un C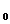- semigrup S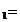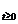al carui generator infinitezimal este A.

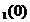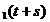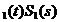Demonstratie. Din principiul lui Banach de inversare, avem ca S, pentru orice t > 0. Observam imediat ca S= I si S=S,pentru orice t , s .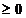

Fie x 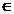X. Din S(1) inversabil rezulta ca exista y 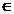X si x S(1)y.

Atunci pentru orice t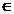 (0,1) avem

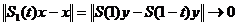, pentru t,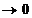

de unde concluzionam ca S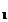 este un C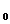- semigrup. Sa notam cu B generatorul sau infinitezimal si fie M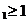 si 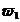> 0 astfel incat

, .

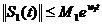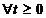Fie x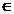 D(A). Avem ca

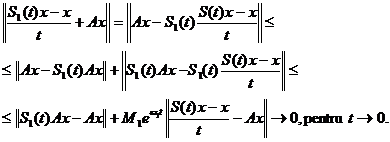
Rezulta ca x 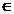D(B) si Bx = 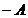x , deci D(A)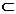 D(B). In mod analog se arata ca

D(B) 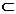D(A), care incheie demonstratia.

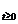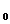Teorema I.1.4. Fie S =un C- semigrup. Urmatoarele afirmatii sunt echivalente:

(i) S poate fi extins la un C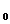- grup;

(ii) exista t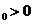astfel incat S(t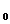) este inversabil;

(iii) pentru orice t>0, S(t) este inversabil.

Demonstratie. (i)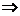(ii) Daca S poate fi extins la grupul U, atunci pentru fiecare

t > 0 avem ca S(t) este inversabil si S(t)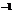= U(-t).

(ii) 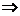(iii) Fie t > 0. Atunci exista n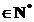 astfel incat n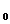t > t.

Din

S(nt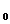)=S(nt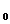-t)S(t)

si S(t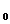) injectiv, rezulta ca S(t) este injectiv. Din

S(nt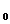)= S(t)S(n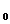t-t

si S(t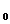) surjectiv , deducem ca S(t) este surjectiv, deci este inversabil.

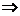(iii)(i) Definim

U(t)=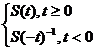

si din Teorema I.1.3. deducem imediat ca 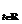este un C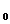- grup.
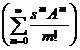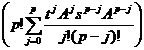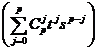
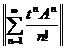
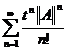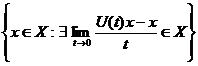