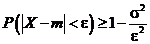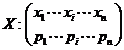 |  |
|
Functii generatoare de momente
Fie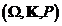 
un
camp borelian de probabilitate si 
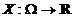o
variabila aleatoare.
Definitia
8. Aplicatia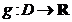 
definita prin 
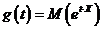se numeste "functia generatoare de momente" a
variabilei aleatoare X, unde D este domeniul maxim de
definitie.
Asadar:
i) Daca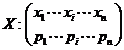 
, atunci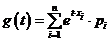 
ii) Daca X are densitatea de
repartitie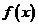 
, atunci
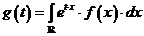
dupa cum variabila aleatoare X este discreta (i) sau continua (ii).
Propozitia
8. Daca variabila
aleatoare X admite momentul initial de ordinul k finit
atunci: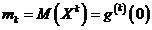 
Inegalitatea lui Cebasev
Daca
variabila aleatoare 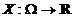are
media m si dispersia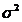 
finite atunci, pentru orice 
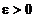, are loc inegalitatea 
Acest document nu se poate descarca
| E posibil sa te intereseze alte documente despre: |
| Copyright © 2025 - Toate drepturile rezervate QReferat.com | Folositi documentele afisate ca sursa de inspiratie. Va recomandam sa nu copiati textul, ci sa compuneti propriul document pe baza informatiilor de pe site. { Home } { Contact } { Termeni si conditii } |
Documente similare:
|
Cauta document |