MINTI
LUMINATE
NR.2/2010

EDITORIAL
Incepand
cu data de 1 octombrie debuteazǎ ,
la noi in scoalǎ, jurnalul de culturǎ matematicǎ "Minti luminate " . Acesta isi
propune sǎ vǎ dezvǎluie partea umanǎ , teoreticǎ
si practicǎ a matematicii . In paginile ei vǎ vom dezvǎlui
lucruri mai putin cunoscute, dar bine pǎstrate , din istoria
matematicii : asa cum au apǎrut , cum ne-au influientat , cum au
ajutat la dezvoltarea matematicii si la ce ne folosesc . Fiecare
numǎr va trata cate un subiect anume si ne-am gandit cǎ cel mai important , interesant
si mai usor pentru viitorul vostru ar fi "Multimile ". Acestea
apar si in programa de evaluare nationalǎ . La sfarsit apar
exercitii de inteligentǎ (IQ). Primul elev care le va rezolva va
primi un "Premiu surprizǎ " . Vǎ invitǎm sǎ veniti cu
articole , probleme , rezolvǎri si propuneri pe care ati dori
sǎ le gǎsiti in ziarul nostru !
SPOR LA
COLABORARE , CITIT SI REZOLVAT !
PSIHOLOGIA MULTIMILOR
De Gustave Le Bon
"Intram
intr-o adevarata era a multimilor" afirma Gustave Le Bon in
cartea "Psihologia multimilor",. "Soarta natiunilor nu se mai
hotaraste in consiliile principilor", spune autorul, "ci in
sufletul multimilor".
Gustave Le Bon (1841-1931),
medic si sociolog francez, s-a numarat printre intelectuali parizieni. Succesul
acestei carti se datoreaza, originalitatii autorului.
Concluziile sale sunt bazate pe
intuitie, ca in cazul afirmatiei: "Multimile sunt feminine, iar
cele mai feminine sunt multimile latine".
Un rol important in
intelegerea multimilor si a modului in care ele
actioneaza, Le Bon il acorda factorilor indepartati, precum
neamul, traditiile, timpul. Totodata autorul a considerat
necesara dedicarea unui capitol special prezentarii
conducatorilor multimilor si a mijloacelor lor de convingere.
Este un aspect deosebit de important, pentru acesti conducatori, care
au detinut si detin inca aceasta pricepere a
manipularii multimilor, folosita in atingerea scopurilor
personale, au mobilizat masele de oameni credincioase lor. Un astfel de conducator
a fost Napoleon Bonaparte. Acest fapt este incontestabil, gandindu-ne numai la
numarul impresionant de soldati pe care i-a convins sa lupte
pentru cauza sa in si pe care i-a trimis la moarte curata in campania
din Rusia. Armata sa intrunea toate caracteristicile unei multimi,
lipsita de ratiune si supusa orbeste iluziilor create
de conducatorul ei. Se pare insa ca Napoleon s-a inselat in
ceea ce priveste multimile spaniole si rusesti.
Cartea se remarca si prin
actualitate.Spre exemplu, "reusita" reclamelor comerciale atat de intens
practicate in zilele noastre isi gaseste o explicatie
deosebit de logica in faptul ca afirmarea repetata a unor texte
simple, duce la implementarea ideii in inconstient. Dupa parerea
mea cartea "Psihologia multimilor" de Gustave Le Bon cuprinde
adevaruri demne de luat in considerare
Prentu Gabriel clsVIII C
Cand
multimile se amuzǎ . .
Vǎ
invit sǎ facem o cǎlǎtorie imaginarǎ in tara
numitǎ "NUMERIA".Aici
trǎiesc in bunǎ pace si intelegere: multimile N; Z;
Q; R.
Sǎ facem cunostintǎ cu
prima multime: N -multimea numerelor naturale.
Purtǎtorul ei de cuvant ne spune: Populatia noastrǎ este
numeroasǎ; nu stim care este cel mai in varstǎ
cetǎtean al acestei multimi , in schimb stim care este cel
mai tanǎr. El se numeste 0. Are o personalitate deosebitǎ: nu se
poate impǎrti sau simplifica cu 0, este elementul neutru in
rǎzboiul cu adunarea.
Sǎ facem cunostintǎ cu
a doua multime Z. Purtǎtorul ei de cuvant
ne declara: ,, Suntem genul acela de numere dintr-o bucatǎ'',la noi nu vei intalni fractiuni sau cifre din
alea aditionale de le zice zecimale.Pe cartea de identitate scrie cǎ
suntem negative sau pozitive. Dar nu uita semnele, cǎ de se intalnesc doua
negative . e cu poveste, nu glumǎ.
Sǎ facem cunostintǎ cu
a treia multime Q:Purtǎtorul ei de cuvant ne declara: Suntem cunoscute sub numele
de fractii si suntem obtinute prin castigarea
rǎzboiului cu impartirea. O fractie ia nastere prin
divizarea a douǎ numere intregi, de aceea noi convetuim atat de bine cu numerele intregi si naturale.
Dupa
cum bǎnuiti mai existǎ si numere ''vanitoase''care
detin controlul peste radical si stǎpanesc zecimalele
neperiodice infinite . Au o bogatie imensǎ: numǎrul pi (π)
si numǎrul de aur..considerate de-a lungul timpului numere
misterioase.
Numǎrul
π=3,1415926535 . are o infinitate de numere
zecimale neperiodice ; s-a introdus ca raportul dintre lungimea cercului
si diametru.Chiar si in Biblie acest numǎr este folosit in lucrarea "Carte I a regilor ,ca fiind 3, cu aproximatie.
π=1-1/3+1/5-1/7 . .Acest numǎr se numeste transcendent, adicǎ
nu poate fi precizat printr-un numǎr finit de operatii algebrice.
Numǎrul de aur Φ.Uriasa piramidǎ a lui Keops cu baza un pǎtrat cu
latura de 230 m si avand inǎltimea de 148m rǎmane o ofrandǎ
vesnicǎ oferitǎ de
preotii egipteni zeilor lor.Ea este mǎrturie a faptului cǎ
printre slujitorii templelor erau multi vrǎjiti de taina
numerelor, care i-au condus sǎ descopere o miniunatǎ proprietate a
raportului dintre douǎ segmente, cunoscutǎ azi sub numele de "
tǎietura de aur ". Numǎrul de aur Φ a fost notat cu litera greceasca FI in amintirea sculptorului Fidias, care a
folosit acest raport in realizarea nemuritoarelor sale opera. Adeptii lui Pitagora considerau
cǎ armonia se exprimǎ prin rapoarte numerice, iar cel ce si-a
insusit intelegerea armoniei devine el insusi nemuritor si
divin. Odatǎ cu aceeastǎ armonie , pitagoricienii au cunoscut o
groaznicǎ dezamǎgire, atunci cand Hippas din Mesopotania a
arǎtat cǎ existǎ mǎrimi care nu pot fi exprimate ca raport
de numere intregi . astfel si-au dezvǎluit personalitatea numerele
irationale.
Astfel ne-am apropiat de a patra
multime R. Purtǎtorul ei de cuvant ne-a declarat: Noi suntem cea
mai bogatǎ multime. Avem in plus si numerele irationale.
Existenta noastrǎ se datoreazǎ lui Hippas care a pornit de la
pǎtratul cu latura de 1 si a arǎtat cǎ diagonala sa nu
poate fi exprimatǎ prin numere rationale. Se credea in antichitate
cǎ dezvǎluind acest secret, el a fost pedepsit de zei si a murit
intr-un naufragiu.Si pitagoricienii si-au adus mai apoi o
contributie deosebitǎ la
dezvoltarea noastrǎ , nu numai a
lui 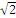 , dar si a altor numere irationale, ca de exemplu
numǎrul de aur,farǎ de care nu s-ar fi putut inscrie pentagonul
regulat in cerc. Mai mult, ducand diagonalele acestui pentagon se obtine pentagrama, figura pe care
pitagoricienii si-au insusit-o ca emblemǎ.Asocierea numǎrului
cosmic cu pentagrama, se datoreazǎ lui Pitagora, care considerǎ
numǎrul 5, ca numǎr perfect al omului, deoarece acesta are 5
simturi, 5 degete la fiecare membru, iar atat inǎltimea cat
si latimea sunt alcǎtuite din 5 pǎrti
egale.Cǎlǎtorului grǎbit . Desi NUMERIA nu apare in niciun
atlas geografic cunoscut panǎ acum, ea este un tǎram mirific, pe care
dacǎ te-ar fi purtat vreodatǎ pasii, cu sigurantǎ vei
dori sǎ te intorci sǎ afli cat mai multe. Cei mai tineri turisti
ai acestei tǎri sunt desigur elevii, care trebuie sǎ fi auzit de
minunatii ei locuitori din manualele scolare.
, dar si a altor numere irationale, ca de exemplu
numǎrul de aur,farǎ de care nu s-ar fi putut inscrie pentagonul
regulat in cerc. Mai mult, ducand diagonalele acestui pentagon se obtine pentagrama, figura pe care
pitagoricienii si-au insusit-o ca emblemǎ.Asocierea numǎrului
cosmic cu pentagrama, se datoreazǎ lui Pitagora, care considerǎ
numǎrul 5, ca numǎr perfect al omului, deoarece acesta are 5
simturi, 5 degete la fiecare membru, iar atat inǎltimea cat
si latimea sunt alcǎtuite din 5 pǎrti
egale.Cǎlǎtorului grǎbit . Desi NUMERIA nu apare in niciun
atlas geografic cunoscut panǎ acum, ea este un tǎram mirific, pe care
dacǎ te-ar fi purtat vreodatǎ pasii, cu sigurantǎ vei
dori sǎ te intorci sǎ afli cat mai multe. Cei mai tineri turisti
ai acestei tǎri sunt desigur elevii, care trebuie sǎ fi auzit de
minunatii ei locuitori din manualele scolare.
Septar Melda si Melek clasa VIII B

Exercitii cu multimi pentru
determinarea IQ-ului .
1.Sa se determine multimile A si
B care indeplinesc simultan conditiile:
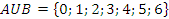
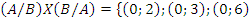

2.Fie A=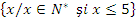
B=
C=
Sǎ se arate cǎ C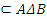
3. Se dau multimil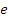

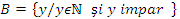
C =
S se g seasc aceste
multimi stiind c elementele lor satisfac relatia :3. = 2.
= 2.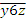
4. Se consider multimile :

B =
S se arate c A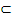 B .
B .
5. Se consider multimile :
A=
B =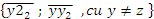 ;
;
C=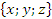 ;
;
S se
determine :
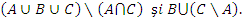
6. Se d A=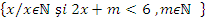
S se determine m , astfel incat :
A s contin exact trei elemente ;
A s contin exact doua elemente ;
A s contin exact un element ;
7. S se
determine num rul de elemente al multimilor
A= ;
;
 C=
C=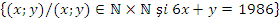
8. S se determine multimile A= si B=
si B= unde a , b , c , d sunt cifre
care indeplinesc conditiile :
unde a , b , c , d sunt cifre
care indeplinesc conditiile :
1) b.c = 12 ;
2) a.d = 5 ;
3) (b+d) -
(a+c)=3 .
9.
S se determine multimele A<B<C , dac sunt
indeplinite simultan conditiile :
a) A b) B
b) B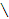 C =
C =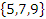 ;
;
c) A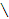 C =
C =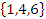 ;
;
d) A B= B
B= B =
= 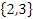 .
.
10.
S se afle valoarea de adev r a propozitiilor :

b) 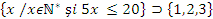 ;
;
c)  =
= 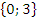 .
.
11. Fie
A = 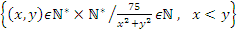 si
si
B= :
:
S se calculeze : A B ;
B ;
Stiati ca .
. In anul 2400 i. Hr.In Mesopotamia se
dezvolta sistemul de numeratie pozitional in baza 60.
Numarul 60 este ales, probabil, ca o consecinta a listei mari de divizori ai acestui numar (adica 12 divizori).
. In anul 585 i. Hr. utilizand proprietatile de
divizibilitate a numerelor, Thales din Milet (636 - 546 i. Hr.) prezice o eclipsa de Soare.
. In anul 500 i. Hr. pitagorienii, lucrand cu numere reprezentate
prin figuri, atribuie cate un sex fiecarui numar, cele impare sunt de
sex masculin, cele pare, de sex feminin. Tot ei introduc notiunile de
numar prim, numar compus, numere relative prime, numere prime
perfecte, numere prietene (amiabile).
. In anul 1200 d. Hr. Leonardo Pisano cunoscut sub numele de Fibonacci scrie lucrarea "Liber
abaci", considerata timp de doua secole cea mai competenta sursa
de cunostinte in teoria numerelor in care sunt prezentate criteriile
de divizibilitate cu 2, 3, 5, 9.
Leonardo da Vinci (15.04.1452 -
2.05.1519) anticipeaza construirea ceasului cu pendul, al carui
mecanism utilizeaza principii de divizibilitate
. In anul 1640 d. Hr. Fermat formuleaza "mica teorema" a numerelor:"Daca p este
un numar prim, atunci orice numar intreg a numarul a p
- a se divide cu p".
. In anul 1772 d. Hr. Christian Goldbach
(8.03.1690 - 20.11.1764) emite ipoteza ca orice numar par mai mare
decat 2 este suma a doua numere prime. Ipoteza nu a fost nici confirmata,
nici infirmata pana in prezent.
. In anul 1850 d. Hr. matematicianul rus Pafnutie Lvovivici
Cebasev (26.05.1821 - 12.08.1894) demonstreaza afirmatia lui
Bertrand: " Pentru orice n numar natural, n > 2, avem cel putin un
numar prim cuprins intre n si 2n - n."
. In anul 1946 d. Hr. se naste calculatorul electronic. Inca de la inceput, puterea
sa de calcul va fi utilizata in cautarea numerelor prime.
. In anul 1959 d. Hr. W. Sierpinski (1882 - 1970) demonstreaza
ca pentru n > 5, intre numerele naturale n si 2n avem cel
putin doua numere prime.
. In anul 1980 d. Hr. L. Adleman si R. Rumelig dezvolta o
metoda noua si imbunatatita de testare a
numerelor in vederea descoperii numerelor prime.
. In anul 1985 Hugh C. Wiliams si
Harvey Dumbar ajung la concluzia ca numarul format din 1031 de cifre
de 1 este prim.
. In anul 2000 d. Hr. Matematicianul american Nayan Hayratwala a lucrat simultan cu mai mult
de 20 de mii de calculatoare de pe intreg globul si a obtinut
numarul prim 2 6 972 593 - 1 fiind cel mai mare numar prim
cunoscut. Pentru scrierea acestui numar sunt necesare doua milioane
de cifre.





