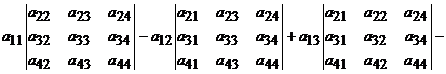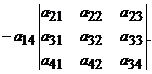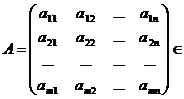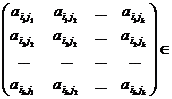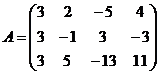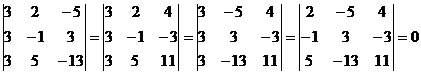Fie M = , N = multimea primelor m,
respective n, numere naturale
nenule. Vom numi matrice de tipul (m,n) o functie A : M N C. Daca notam A(i,j) = c, vom nota pe A sub forma
(1)
Adica printr-un tablou cu m
linii si n coloane ce cuprinde valorile functiei A. Datorita
notatiei (1), in loc de matrice de tipul (m,n) se mai spune matrice cu m linii si n coloane. Numerele se numesc elementele matricei A. De multe ori pentru matricea A se mai
foloseste notatia prescurtata:
sau
Se observa ca o matrice de tipul (m,n) are mn elemente.
Cazuri particulare:
I). Daca n =1,
o matrice de tipul (m,1) se numeste
matrice coloana si este de forma
II). Daca m =1,
o matrice de tipul (1,n) se numeste
matrice - linie si este de forma
III). Daca m = n,
o matrice de tipul (n,n) se numeste
matrice patratica de ordinul n.
Daca
este o matrice patratica de ordinul n, sistemul ordonat de elemente se numeste diagonala principala a matricei A, iar sistemul ordonat de
elemente se numeste diagonala secundara a matricei.
Matricea care se obtine din matricea A schimband in aceasta
liniile cu coloanele se numeste transpusa matricei A si se noteaza At
.
Exemple.
1)
2)
Adunerea
matricelor se face pe componente iar inmultirea cu scalari se face inmultind
fiecare element al matricei cu acel
scalar.
Definitie.
Numarul unde S
este multimea tuturor permutarilor de gradul n si este signatura permutarii se numeste determinantul matricei A sau, mai simplu, determinantul de ordin n si se noteaza astfel:
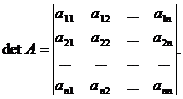
Produsul 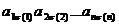 se numeste termen al determinantului de ordin n. se numeste termen al determinantului de ordin n.
Cazuri particulare.
. Fie A
o matrice de ordin trei cu coeficienti reali, A=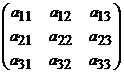 , determinantul matricei A, notat detA sau , determinantul matricei A, notat detA sau 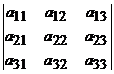 este un numar care se calculeaza astfel: este un numar care se calculeaza astfel:
detA=a11a22a33+ a13a21a32+
a12a23a31- a13a22a31-
a21a12a33- a11a32a23.
Daca matricea este de
ordinul 4, atunci se dezvolta dupa o linie sau o coloana (de obicei prima
linie)
in 4 determinanti
de ordin 3. Fie A=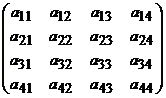 , ,
det A=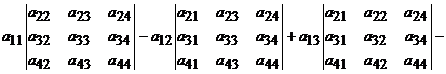
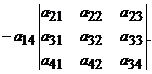
Proprietati.
Determinantul unei matrice coincide cu determinantul
matricei transpuse.
Daca toate elementele unei linii (coloane) sunt nule,
atunci determinantul matricei este nul.
Daca intr-o matrice schimbam doua linii (coloane) intre
ele, obtinem o matrice care are determinantul egal cu opusul determinantului matricei initiale.
Daca o matrice are doua linii (coloane) identice, atunci
determinantul sau este nul.
Daca toate elementele unei linii (coloane) ale unei
matrice A sunt
inmultite cu un element a obtinem
o matrice al carui determinant este
egal cu a inmultit cu determinantul
matricei initiale.
Daca elementele a doua linii (coloane) ale unei matrice
sunt proportionale, atunci determinantul matricei este nul.
RANGUL UNEI MATRICE
Sa consideram o matrice A cu m linii si n
coloane cu elemente numere complexe,
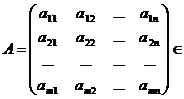 M M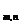 (C), (C),
iar k un
numar natural, astfel incat 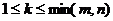 ( prin min(m,n) intelegem cel mai mic dintre
numerele m si n). ( prin min(m,n) intelegem cel mai mic dintre
numerele m si n).
Daca
in A alegem k linii: 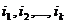 si k coloane: si k coloane: 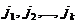 ,
elementele care se gasesc la intersectia acestor linii si coloane formeaza o
matrice patratica de ordin k: ,
elementele care se gasesc la intersectia acestor linii si coloane formeaza o
matrice patratica de ordin k:
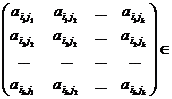 M M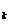 C), C),
al carei determinant se numeste minor de ordin k al matricei A.
Sa consideram 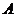 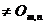 o matrice cu m linii si n coloane. Cum matricea A are elemente nenule, exista minori nenuli de un anumit
ordin o matrice cu m linii si n coloane. Cum matricea A are elemente nenule, exista minori nenuli de un anumit
ordin 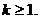 Dar multimea minorilor matricei A fiind
finita este evident ca exista un numar natural Dar multimea minorilor matricei A fiind
finita este evident ca exista un numar natural 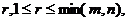 astfel incat sa avem cel putin un minor de
ordin r nenul, iar toti minorii de ordin mai mare decat r ( daca exista) sa fie nuli. astfel incat sa avem cel putin un minor de
ordin r nenul, iar toti minorii de ordin mai mare decat r ( daca exista) sa fie nuli.
Definitie. Fie A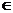 M M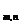 (c)
o matrice nenula. Spunem ca matricea A are
rangul r, si scriem rangA=r, daca A are un minor nenul de ordin r,
iar toti minorii lui A de ordin mai
mare decat r ( daca exista) sunt
nuli. (c)
o matrice nenula. Spunem ca matricea A are
rangul r, si scriem rangA=r, daca A are un minor nenul de ordin r,
iar toti minorii lui A de ordin mai
mare decat r ( daca exista) sunt
nuli.
Daca A este matricea nula, convenim sa
spunem ca matricea are rangul 0, adica rang(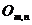
Pentru calculul rangului unei matrice este utila
teorema urmatoare.
Teorema. Fie 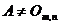 , o matrice. Numarul
natural r este rangul matricei A daca si numai daca exista un minor de ordin
r al lui A, nenul, iar toti minorii de ordinul r+1 , o matrice. Numarul
natural r este rangul matricei A daca si numai daca exista un minor de ordin
r al lui A, nenul, iar toti minorii de ordinul r+1
(daca
exista) sunt nuli.
Aplicatie.
Sa se calculeze rangul matricei
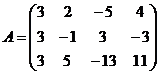
Rezolvare.
Exista minori de ordinul al doilea nenuli, ca de
exemplu:
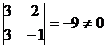
Calculam minorii de ordinul al treilea ai matricei A si gasim ca toti sunt nuli:
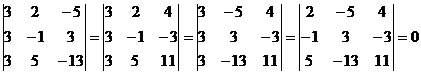 .
Deci rangul matricei rang A=2. .
Deci rangul matricei rang A=2.
|


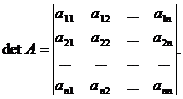
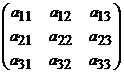 , determinantul matricei A, notat detA sau
, determinantul matricei A, notat detA sau 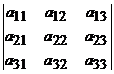
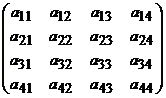 ,
,