PROBLEMA DE PROGRAMARE
LINIARA (PPL)
Forme
fundamentale ale PPL, solutii, clasificare; interpretarea economica a
PPL.
O problema de programare matematica reprezinta
determinarea optimului (maximului sau minimului) unei functii de
variabila vectoriala care indeplineste anumite conditii
(restrictii, legaturi) de tip inecuatii sau ecuatii, precum
si conditii de nenegativitate ale variabilelor functiei.
Daca toate functiile care intervin in formularea problemei de
programare matematica sunt liniare, atunci problema se numeste problema de programare liniara
(PPL); in caz contrar se numeste problema
de programare neliniara.
1)
Forma standard - este cea care contine
restrictii de tip ecuatii.
- optim z=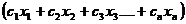
-restrictii de tip egalitate: 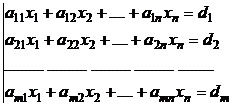
- conditii de nenegativitate: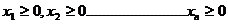
Matricial forma standard poate fi
exprimata astfel :
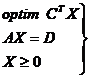 unde
unde 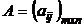
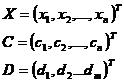
Observatii:
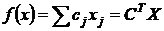 - se numeste functie obiectiv ( functia
economica)
- se numeste functie obiectiv ( functia
economica)
spatiul Rn al vectorului X ,respectiv C -
se numeste spatiul activitatilor
vectorul 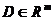 se numeste vectorul
resurselor
se numeste vectorul
resurselor
spatiul Rm se numeste spatiul
resurselor.
2)
Forme canonice 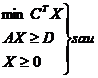
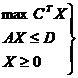
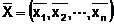 care verifica
sistemul de restrictii se
numeste solutia problemei
(solutie posibila);
care verifica
sistemul de restrictii se
numeste solutia problemei
(solutie posibila);
- o solutie 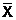 a
restrictiilor care verifica conditiile de nenegativitate se
numeste program sau solutie admisibila;
a
restrictiilor care verifica conditiile de nenegativitate se
numeste program sau solutie admisibila;
- programul 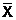 pentru care se
realizeaza extremul solicitat al functiei se numeste program optim.
pentru care se
realizeaza extremul solicitat al functiei se numeste program optim.
Fie problema de programare liniara in forma standard.
Se poate ca restrictiile de tip inegalitate
sa fie aduse la forma unor restrictii de tip egalitate prin adunarea
(sau scaderea) in unul din termenii inegalitatii a unui termen
numit variabila ecart sau
variabila de compensare.
Presupunem rang A =m si m<n
Rezulta ca sistemul de restrictii este compatibil nedeterminat
si s-a presupus eliminarea ecuatiilor secundare.
Notam 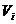 -vectorii coloana
-vectorii coloana 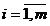 ai matricei A ,
ai matricei A , 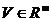 ; atunci sistemul de restrictii se poate scrie:
; atunci sistemul de restrictii se poate scrie:
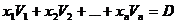
Fie
B o baza in spatiul 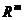 . Notam
. Notam 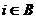 pentru
pentru 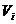 unul din vectorii bazei B. Fie
unul din vectorii bazei B. Fie 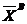 este solutia de baza corespunzatoare bazei B. O baza B care conduce la un
program se numeste baza admisibila; daca
este solutia de baza corespunzatoare bazei B. O baza B care conduce la un
program se numeste baza admisibila; daca 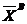 nu este program ,zicem ca B este posibila.
nu este program ,zicem ca B este posibila.
Modele de programare liniara
intalnite in practica economica
Dintre cele mai intalnite
probleme cu caracter economic modelate cu ajutorul programarii liniare le
prezentam pe urmatoarele:
a) problema de
planificare a productiei
O intreprindere produce n sortimente 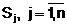 si dispune de
m resurse
si dispune de
m resurse 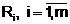 . Se cere sa se organizeze productia daca
se cunosc cantitatea de resurse disponibile, consumurile specifice si
beneficiile unitare.
. Se cere sa se organizeze productia daca
se cunosc cantitatea de resurse disponibile, consumurile specifice si
beneficiile unitare.
Identificam organizarea productiei in crearea
modelului PPL cu planul de productie.
Fie: di - cantitatea de resurse Ri
disponibila
aij - cantitatea de resurse Ri necesare consumarii
pentru sortimentul Sj
cj - beneficiul adus de sortimentul Sj.
Notam xj - numarul de sortimente de tip Sj.
Atunci planul de productie este reprezentat de vectorul coloana 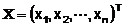
Deci PPL se poate enunta astfel:
Sa se determine
coordonatele 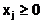 ale lui
ale lui 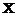 in conditiile:
in conditiile:
1) nedepasirea resurselor
3) obtinerea unui beneficiu
maxim
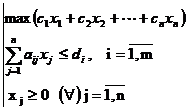
b) problema de nutritie
O dieta trebuie sa contina
substante nutritive 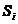 in cantitatile
in cantitatile 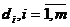 ,ce se gasesc in alimentele
,ce se gasesc in alimentele 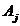
Fie aij - cantitatile de substanta 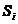 continuta in alimentul Aj
,
continuta in alimentul Aj
,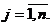
cij-costul unitar al
alimentului Aj.
Sa se determine cantitatile xj de alimente necesare asigurarii
nivelului cerut de substante 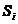 astfel incat costul total al dietei sa fie minim.
astfel incat costul total al dietei sa fie minim.
Modelul matematic al problemei: 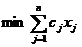 astfel incat
astfel incat 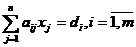
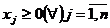
c) Problema de transport
Acelasi produs trebuie redistribuit de
la m -centre de productie ( furnizor)
catre n-centre de desfacere (beneficiar ),disponibilul furnizorului 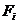 este
este 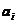 ,necesarul beneficiarului Bj
este bj, costul unitar de la furnizorul
,necesarul beneficiarului Bj
este bj, costul unitar de la furnizorul 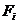 catre beneficiarul Bj este cij . A organiza transportul revine la a
determina cantitatile de produs ce trebuiesc transportate de la fiecare
furnizor catre fiecare beneficiar astfel incat costul total al
transportului sa fie mimim.
catre beneficiarul Bj este cij . A organiza transportul revine la a
determina cantitatile de produs ce trebuiesc transportate de la fiecare
furnizor catre fiecare beneficiar astfel incat costul total al
transportului sa fie mimim.
Notam xij -cantitatea ce
se transporta de la furnizorul 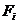 la beneficiarul Bj.
la beneficiarul Bj.
Considerand ca totalul disponibil la
furnizori este egal cu totalul necesar la beneficiari, problema devine echilibrata
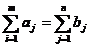 iar modelul de programare liniara este :
iar modelul de programare liniara este :
min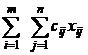
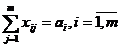
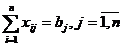
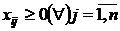
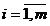
d) Problema de amestec
Un produs se obtine din amestecul a n- materii
prime Mj , unitatea de materii prime Mj contine aij
unitati de substanta 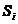
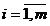 . Produsul trebuie sa contina cel putin dh ,
. Produsul trebuie sa contina cel putin dh , 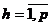 unitati de substanta
unitati de substanta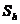 si cel mult dk,
si cel mult dk, 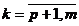 unitati de substanta
unitati de substanta 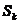 ,costul unitar al materiilor prime Mj este cj .
,costul unitar al materiilor prime Mj este cj .
Sa se determine xj cantitatile de materii prime Mj ce
trebuie sa intre in componenta produsului astfel incat costul lui sa fie minim.
Modelul matematic al problemei
formulat ca o PPL este:
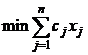
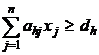 ,
,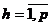
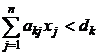 ,
,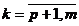
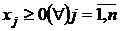


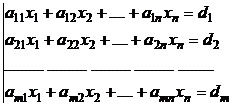
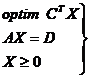
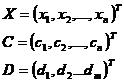
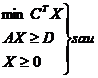
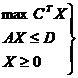
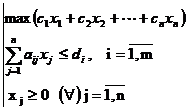
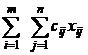
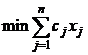
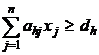 ,
,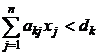 ,
,