Procedeul Gramm-Scmidt de determinare a unei baze
ortornomate
Pornind de la baza B= vom
construi mai intai o baza formata din
elemente ortogonale pe care mai apoi le normam.
Pasul 1. Se ia w1 =
v1.
Pasul 2. Se considera w2 = v2 + 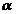 w1. Vectorul w2 este nenul deoarece v1 si v2
sunt liniar independenti. Vom
determina scalarul w1. Vectorul w2 este nenul deoarece v1 si v2
sunt liniar independenti. Vom
determina scalarul 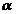 astfel incat w2 si w1 sa fie ortogonali si atunci multimea este liniar independenta. astfel incat w2 si w1 sa fie ortogonali si atunci multimea este liniar independenta.
0=<w2,w1> = <v2
+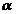 w1, w1>=<v2, w1>+ w1, w1>=<v2, w1>+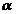 <w1, w1>. <w1, w1>.
Deci 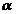 = - <v2,w1>
/ <w1, w1>, avem ca w2 = v2 -
(<v2, w1> / <w1, w1>)
w1 si folosindu-ne de definitiile anterioare avem ca w2 se obtine scazand din v2 proiectia lui v2
pe w1. = - <v2,w1>
/ <w1, w1>, avem ca w2 = v2 -
(<v2, w1> / <w1, w1>)
w1 si folosindu-ne de definitiile anterioare avem ca w2 se obtine scazand din v2 proiectia lui v2
pe w1.
Pasul 3. Consideram w3 = v3+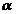 1w1+ 1w1+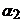 w2, care
este nenul pentru ca sunt liniar independenti, iar scalarii w2, care
este nenul pentru ca sunt liniar independenti, iar scalarii 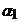 , , 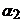 , se determina astfel incat w3 sa fie
ortogonal cu w1 si w2. , se determina astfel incat w3 sa fie
ortogonal cu w1 si w2.
0=<w3, w1>
= <v3, w1> +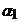 <w1, w1> + <w1, w1> + 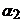 <w2, w1>. Cum <w2, w1> = 0 rezulta ca <w2, w1>. Cum <w2, w1> = 0 rezulta ca 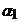 = - <v3, w1> / <w1,
w1 >. = - <v3, w1> / <w1,
w1 >.
0=<w3, w2>=<v3,
w2> + 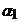 <w1, w2 > + <w1, w2 > + 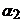 <w2 , w2>. <w2 , w2>.
Cum <w2, w1> = 0 rezulta 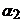 = - (<v3, w2> / <w2,
w2>). = - (<v3, w2> / <w2,
w2>).
Deci avem ca:
w3=v3 - (<v3, w1> / <w1,
w1> ) w1 - (<v3, w2> / <w2,
w2>) w2 adica
w3 se obtine sca zand din v3 proiectiile lui v3 pe w1
si pe w2.
Deoarece w1, w2, w3 sunt ortogonali doi cate doi, avem ca multimea este liniar independenta.
Pasul j. Presupunem ca am determinat vectorii w1, w2,,w(j-1).
Vom determina vectorul wj
de forma: wj = vj + 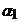 w1 + w1 + 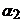 w2 +
+ w2 +
+ 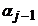 w w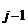 , ,
unde scalarii 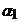 , , 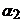 , , , ,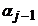 se determina se determina
astfel incat wj sa fie
ortogonal cu w1,
w2,,wj-1.
Deci, din conditiile <wj, wi>= 0, pentru
orice i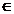 , rezulta , rezulta
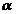 i= -(<vj, wi> / <wi,
wi>, pentru orice i i= -(<vj, wi> / <wi,
wi>, pentru orice i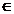 . Atunci
rezulta ca: wj = vj-[(<vj,
w1> )/(<w1 , w1>)]w1- (<vj,
w2>/<w2, w2>)w2- - (<vj,
w(j-1)>/ <w(j-1), w(j-1)>)w(j-1). . Atunci
rezulta ca: wj = vj-[(<vj,
w1> )/(<w1 , w1>)]w1- (<vj,
w2>/<w2, w2>)w2- - (<vj,
w(j-1)>/ <w(j-1), w(j-1)>)w(j-1).
Dupa n pasi, repetand procedeul anterior, obtinem n vectori ortogonali, deci liniar independenti, deci o baza formata din
vectori ortogonali. Pentru a gasi baza
ortonormata vom considera vectorii: ei= wi / ||wi||, i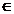 . .
Procedeul descris se
numeste procedeul de ortogonalizare GRAM-SCHMIDT.
Exemplu. Folosind procedeul Gram-Schmidt sa se gaseasca o baza ortonormata in R3 pornind de la baza B=, v1 = (1,1,1),
v2 = (1,2,3,), v3 =(1,0,2).
Pasul 1. w1 = v1 = (1,1,1).
Pasul 2. w2 =
v2 + 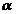 w1. w1.
0 = <w2, w1
> = <v2 + 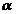 w1, w1> = <v2, w1
> + w1, w1> = <v2, w1
> + 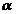 <w1, w1 >. <w1, w1 >.
Dar <v2 , w1> =1x
1+1x 2+1x 3=1+2+3=6 si <w1, w1 > = 1+1+1=
3, deci 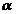 = -6/3 =-2. = -6/3 =-2.
Avem w2 = (1,2,3) + (-2,-2,-2) = (-1,0,1)
deci w2 = (-1,0,1).
Pasul 3. w3 =
v3 + 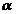 1w1 + 1w1 + 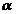 2 w2 , 0 = <w3 , w3>
= <v3 , w2> + 2 w2 , 0 = <w3 , w3>
= <v3 , w2> +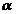 1<w1, w2 > + 1<w1, w2 > +
+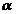 2 <w2, w2>. Dar
<w1, w2 > = 0 si <w2, w2 >
= (-1)2 +02 +12 = 2, <v3, w2
> = 1x (-1)+ 2 <w2, w2>. Dar
<w1, w2 > = 0 si <w2, w2 >
= (-1)2 +02 +12 = 2, <v3, w2
> = 1x (-1)+
0x 0+2x1=1, de unde rezulta:
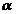 2=1 / 2. 2=1 / 2.
0 = <w3, w1
> = < v3 , w1 > + 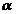 1 < w1, w2 > + 1 < w1, w2 > + 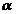 2<w2, w1 >. 2<w2, w1 >.
Dar <w2, w1 > = 0 si <v3
, w1 > = 1x 1 + 0x 1 + 2 x 1=3, deci 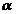 1 = -1. 1 = -1.
Atunci: w3 = (1,0,2) - (1,1,1) - 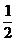 (-1,0,1) = ( (-1,0,1) = (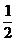 , -1, , -1, 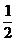 ) . ) .
Deci avem baza ortogonala
este
baza ortonormata cautata.
|

