|
Ce este un spatiu vectorial Euclidian?
|
Definitia 1. Fie V un spatiu vectorial complex. Se numeste produs scalar o aplicatie < , > : V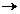 C care are
proprietatile: C care are
proprietatile:
i) <v,w>=<w,v>, 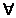 v,w v,w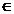 V; V;
ii) <u, v+w>=<u, v>+<u, w>, 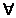 u,v,w u,v,w 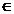 V; V;
iii) a<v,w>=<av,w>, 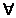 a a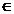 C si C si 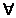 u,v u,v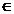 V; V;
iv) <v,v>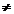 0 si <v,v>=0
daca si numai
daca v=0. 0 si <v,v>=0
daca si numai
daca v=0.
Observatia 2 Produsul
scalar are proprietatile:
i) <v,aw>=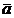 <v,w>, a <v,w>, a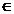 C, v, w C, v, w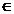 V. V.
ii) <u+v, w>=<u, w>+<v, w>, u,v,w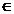 V. V.
iii) Daca <x, y>=0, 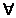 y y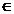 V V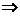 x=0 si daca <x,y>=<z,y>, pentru orice y x=0 si daca <x,y>=<z,y>, pentru orice y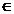
V, atunci x=z.
Un spatiu vectorial
(real sau complex) pe care s-a definit un produs scalar se numeste spatiu vectorial Euclidian (real
sau complex).
Observatia 3 1) Daca V este spatiu vectorial real,
atunci axioma i) din Definitia 1. devine
<v,w>=<w,v>, iar relatia <v, 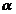 w>= w>=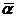 <v,w>
devine <v, <v,w>
devine <v, 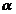 w>= w>= 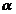 <v,w>. <v,w>.
2) Orice subspatiu vectorial al unui spatiu vectorial Euclidian este la randul sau euclidian, produsul scalar fiind
acelasi.
Exemple:
R2 impreuna cu produsul
scalar <x,y>=x1y1+x2y2,
unde x=(x1, x2),
y=(y1, y2)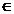 R2
este spatiu vectorial Euclidian real. R2
este spatiu vectorial Euclidian real.
R3 impreuna cu produsul
scalar <x,y>=x1y1+x2y2+x3y3,
unde x=(x1, x2,, x3), y=(y1,
y2,, y3)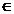 R3 este spatiu vectorial Euclidian
real. R3 este spatiu vectorial Euclidian
real.
Definitia 4.
Fie V un spatiu vectorial real sau complex.
Spunem ca aplicatia
||, ||: V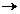 R+ este o norma
pe V daca satisface urmatoarele conditii pentru R+ este o norma
pe V daca satisface urmatoarele conditii pentru 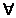 x,y x,y 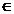 V, V,
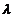 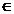 K: K:
1) ||x|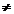 0 si ||x||=0 daca si numai daca x=0. 0 si ||x||=0 daca si numai daca x=0.
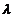 x||=|
x||=|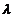 | ||x||. | ||x||.
3)
||x+y||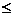 ||x||+||y||. ||x||+||y||.
Un
spatiu vectorial pe care s-a definit o norma se numeste spatiu
normat.
Exemple: 1) R ca R-
spatiu vectorial este normat, cu
functia valoare absoluta ca norma.
2. C este R-spatiu vectorial normat
cu functia modul.
Propozitia 5. Orice spatiu vectorial Euclidian
este normat. Norma obtinuta se numeste norma
Euclidiana.
Observatia
6. 1) Din primele doua proprietati ale
normei rezulta ca orice vector v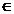 V se poate scrie sub forma: v=||v||
e , unde ||e||=1. Vectorul e
cu aceasta proprietate se numeste versor.
Deci versorul asociat unui vector
nenul v are expresia: e= V se poate scrie sub forma: v=||v||
e , unde ||e||=1. Vectorul e
cu aceasta proprietate se numeste versor.
Deci versorul asociat unui vector
nenul v are expresia: e=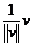
2)
Fie V spatiu Euclidian real si v,w doi vectori
nenuli.
Inegalitatea
Cauchy-Schwarz: <v,w>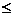 ||v|| ||w||
||v|| ||w||
Suntem in masura acum sa definim unghiul a doi vectori nenuli.
Definitia 6.
Fie V
spatiu Euclidian real si v,w doi vectori nenuli din V. Numarul 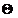 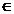 [0 [0 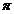 ] definit de egalitatea cos ] definit de egalitatea cos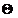 =<v,w>/||v|| ||w|| se numeste unghiul dintre v
si w. =<v,w>/||v|| ||w|| se numeste unghiul dintre v
si w.
Definitia 7. Fie V
o multime nevida. O functie
d:
V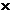 V V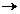 R+ care satisface conditiile: R+ care satisface conditiile:
1) d(u,v)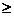 0; d(u,v)=0 0; d(u,v)=0 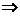 u=v, u=v,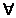 u,v u,v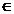 V, V,
2) d(u,v)=d(v,u), 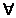 u,v u,v 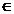 V, V,
3) d(u,v)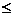 d(u,w)+d(w,v), d(u,w)+d(w,v), 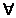 u,v,w u,v,w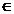 V, V,
se numeste distanta sau metrica pe V.
O
multime nevida inzestrata cu o functie distanta se numeste spatiu metric.
Propozitia 8. Fie V un spatiu
vectorial normat. Functia reala d:
V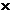 V V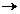 R+,
definita prin d(u,v)=||u-v||, este o distanta pe V. R+,
definita prin d(u,v)=||u-v||, este o distanta pe V.
Se
observa ca orice spatiu vectorial normat este metric si ca orice spatiu vectorial
Euclidian care este normat este metric.
|

