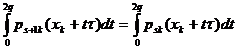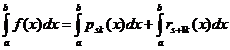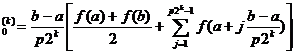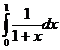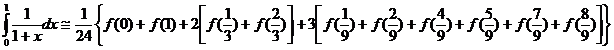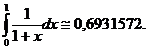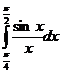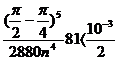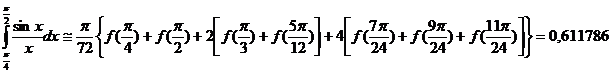Formulele
Newton-Cotes de tip inchis
Fie h=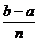 , n
, n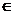 N
N și x
și x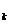 =a+kh,
=a+kh, 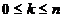 .
.
Avem:
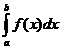 =
=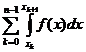 .
.
Pe fiecare
interval 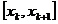 ,
, 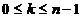 , consideram punctele echidistante :
, consideram punctele echidistante :
x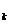 +i
+i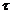 ,
, 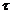 =
=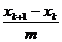 ,
, 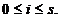
Pe acest sistem de noduri
consideram formula de interpolare a lui Newton:
f=p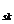 +r
+r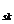 , unde :
, unde :
p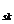 (x)=f(x
(x)=f(x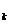 )+
)+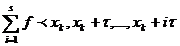 >
>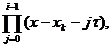
r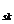 (x)=f<x,
(x)=f<x,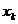 ,x
,x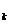 +
+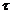 ,,x
,,x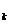 +s
+s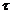 >
>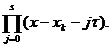
Pentru diferențele divizate folosim
formula de calcul cu ajutorul diferențelor ascendente:
f<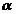
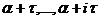 >=
>=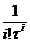
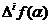
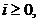
Se efectueaza in (9) și (10)
schimbarea de variabila x=x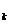 +t
+t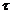
Obținem:
p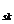 (x
(x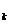 +t
+t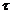 )=f(x
)=f(x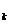
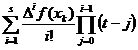
r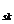 (x
(x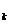 +t
+t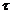
 f(x
f(x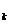
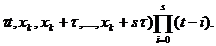
Remarca. In (12) pasul
diferențelor ascendente este 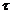
Daca f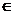 C
C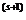
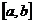 , exprimand diferența divizata din (13) cu ajutorul derivatei de
ordinul s+1, obținem:
, exprimand diferența divizata din (13) cu ajutorul derivatei de
ordinul s+1, obținem:
r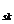 (x
(x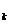 +t
+t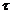 )=
)=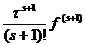 (C
(C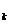 (t))
(t))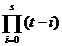 ,
,
unde C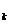 este un punct intermediar punctelor x
este un punct intermediar punctelor x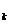 +t
+t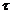 , x
, x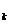 +i
+i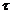 ,
, 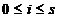 .
.
Avem:
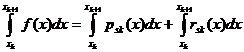 .
.
In ambele
integrale din membrul drept efectuam schimbarea de variabila x=x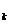 +
+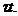
Obținem:
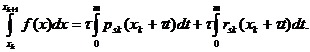
Utilizand (12) rezulta:
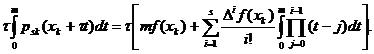
Deoarece 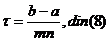 și (15) rezulta:
și (15) rezulta:
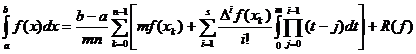 ,
,
unde:
R(f)=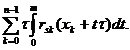
Formula
(16) reprezinta forma generala a formulelor Newton Cotes de tip
inchis.
Pentru
studiul restului presupunem ca f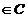
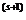
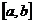 . In acest caz avem:
. In acest caz avem:
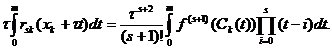
Deci:
R(f)=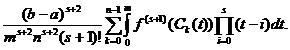
Cazuri particulare.
I.
Formula generalizata a trapezelor.
Aceasta
fprmula se obține pentru m=s=1. Rezulta 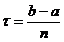
Din (16) deducem:
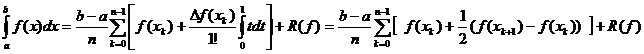 Pentru n
Pentru n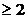 se obține formula :
se obține formula :
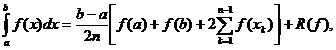
(formula generalizata a trapezelor).
Pentru
n=1 se obține formula clasica a trapezelor:
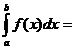
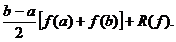
Studiul
restului. Din (18) rezulta:
R(f)=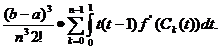
Folosind formula de medie pentru integrala,
obținem:
R(f)=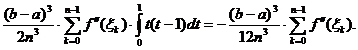
Deoarece f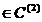
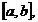 rezulta ca exista un punct
rezulta ca exista un punct 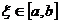 , astfel incat :
, astfel incat : 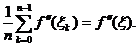
Obținem in final pentru rest expresia:
R(f)=-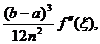
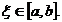
II.
Formula generalizata a lui Simpson.
Aceasta formula se obține pentru
m=2, s=3. In acest caz avem 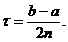 Din (16) rezulta:
Din (16) rezulta:
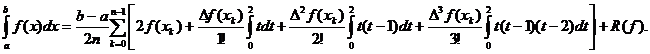 Ultima integrala are valoarea zero. Apoi:
Ultima integrala are valoarea zero. Apoi:

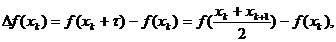
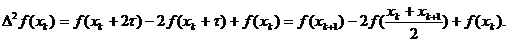
Pentru n dupa un calcul elementar, se obține formula:
dupa un calcul elementar, se obține formula:
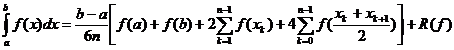
(formul
generalizata a lui Simpson).
Pentru n=1 se obține formula
clasica a lui simpson:

Studiul restului. Din (18) rezulta:
R(f)=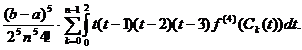
Cu
toate ca t(t-1)(t-2)(t-3) nu pastreaza semn constant pe 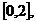 se poate arata ca R(f) se
poate scrie sub forma:
se poate arata ca R(f) se
poate scrie sub forma:
R(f)=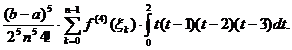
Se obține in final pentru rest evaluarea:
(22) R(f)=-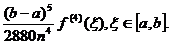
III. Formula generalizata a lui Newton.
Aceasta formula se obține pentru m=s=3. In
acest caz avem:
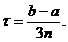 Din (16) rezulta:
Din (16) rezulta:
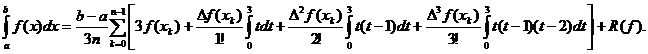 Deoarece:
Deoarece:

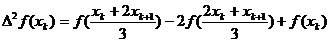
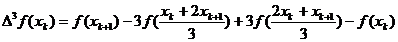
dupa inlocuiri, pentru 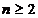 rezulta formula:
rezulta formula:
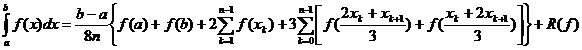
(formula
generalizata a lui Newton).
Pentru
n=1 se obține formula clasica a lui Newton:
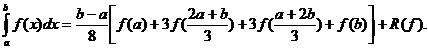
Studiul
restului. Din (18) rezulta:
R(f)=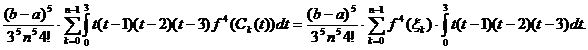
Deoarece f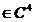
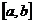 , rezulta ca exista
, rezulta ca exista 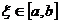 cu proprietatea :
cu proprietatea :
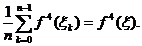
In final se obține pentru rest expresia:
R(f)=- 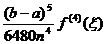 ,
, 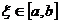 .
.
Comentarii.
1 . Pentru m=2q se poate
lua s=m+1. Avem:
. Pentru m=2q se poate
lua s=m+1. Avem:
p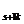 (x
(x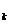 +t
+t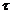 )=p
)=p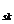 (x
(x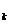 +
+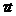 )+
)+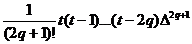 f(x
f(x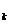 ).
).
Deoarece:
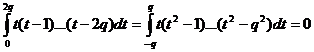 ,
,
rezulta:
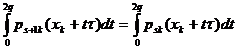
și deci:
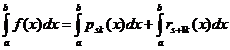
Formula
(25) este exacta pentru polinoame de grad cel mult 2q+1.
Pentru
m=s=2q+1 se obțin formule exacte pentru polinoame de grad cel mult 2q+1.
Din
aceste motive, de obicei se prefera aplicarea formulelor de integrare
numerica pentru m par.
 Numarul n al punctelor
Numarul n al punctelor 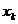 se alege astfel incat
valoarea absoluta a restului sa fie mai mica decat eroarea admisa.
De exemplu, pentru a aproxima valoarea integralei
se alege astfel incat
valoarea absoluta a restului sa fie mai mica decat eroarea admisa.
De exemplu, pentru a aproxima valoarea integralei 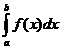 cu eroarea data
cu eroarea data 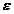 , folosind formula lui Newton (23), procedam astfel:
, folosind formula lui Newton (23), procedam astfel:
a) Daca se
poate calcula numarul M=sup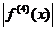 , sau un majorant al acestuia
, sau un majorant al acestuia 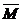 , atunci
, atunci
x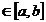
vom lua pentru n cel mai mic numar
natural cu proprietatea:
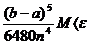 , respectiv
, respectiv 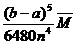

Cu n astfel determinat, vom aproxima
valoarea integralei cu primul termen al membrului drept din formula (23).
b)
Daca nu se poate calcula M și nici un majorant al acestuia, atunci
pentru valori crescatoare ale lui n(obținute printr-un algoritm
oarecare) calculatorul ne va da un șir de valori, aproximații pentru
integrala. Pentru n suficient de mare, diferența in valoare
absoluta intre doua valori consecutive va fi mai mica decat 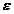 . Calculele pot fi oprite in acest moment.
. Calculele pot fi oprite in acest moment.
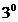 . Formula lui Romberg. Formula:
. Formula lui Romberg. Formula:
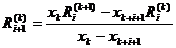
din algoritmul de accelerare al lui
Richardson, (formula (5) din capitolul IV), pentru x
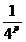 , devine:
, devine:
 , i
, i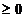 , k
, k
Fie
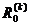 aproximațiile integralei
aproximațiile integralei 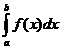 , calculate cu formula trapezelor (19), unde n=p2
, calculate cu formula trapezelor (19), unde n=p2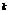 , p
, p . Deci:
. Deci:
R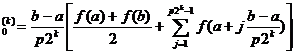
Metoda descrisa de formulele (26)
și (27) se numește metoda lui
Romberg.
Exemplul 1. Sa se
aproximeze valoarea integralei 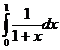 cu eroarea
cu eroarea 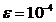 , cu formula lui Newton.
, cu formula lui Newton.
Soluție. f(x)=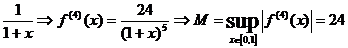
Condiția 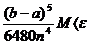 este echivalenta aici cu :
este echivalenta aici cu : 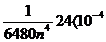
Rezulta n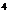
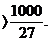 Cel mai mic numar natural cu aceasta proprietate este 3. Vom lua n=3. Deci: x
Cel mai mic numar natural cu aceasta proprietate este 3. Vom lua n=3. Deci: x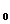 =0, x
=0, x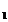 =
=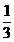 , x
, x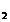 =
=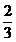 ,
, 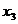 =1.
=1.
Obținem:
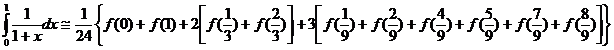
Rezulta: 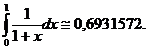
Valoarea exacta a integralei este
ln2=0,69314718056.
Exemplul 2. Sa se
calculeze 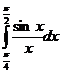 cu o eroare
cu o eroare 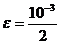 , folosind formula lui Simpson.
, folosind formula lui Simpson.
Soluție. Derivata a patra a funcției f(x)=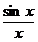 este :
este :
f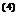 (x)=
(x)=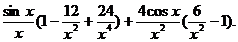
Cei
doi termeni din expresia lui f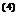 sunt pozitivi și descrescatori pe intervalul
sunt pozitivi și descrescatori pe intervalul 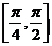
Rezulta 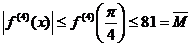
Din:
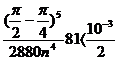 rezulta n
rezulta n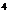
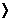 16,8. Vom lua n=3.
16,8. Vom lua n=3.
Deci: x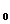 =
=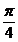 , x
, x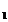 =
=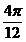 , x
, x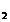 =
= , x
, x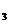 =
=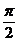 .
.
Obținem:
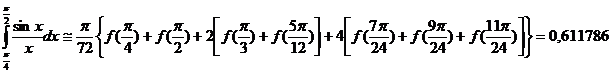
Folosind al doilea procedeu se obțin
rezultatele din tabelul urmator:
|
n
|
I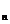
|
|
|
Exemplul 3. In tabelul urmator sunt
trecute rezultatele obținute aplicand formula lui Simpson pentru
integrala:

Folosind al doilea procedeu, cu 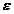 precizat.
precizat.
|
n
|
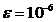
|
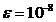
|
|
|
|
Exemplul 4. Pentru integrala:
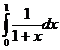
din exemplul 1, aplicam acum
metoda lui Romberg (26)+(27), cu p=1.
In tabelul care urmeaza apar primele patru coloane din
tabloul lui Richardson:
Valoarea exacta a integralei, cu 11 zecimale, este
0,69314718056.
Primele
trei zecimale exacte, in prima coloana se obțin pentru k=4, deci prin
insumarea a 2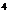 -1=15 termeni in (27). Cu același numar de termeni, se obțin
in coloana a patra 8 zecimale exacte in R
-1=15 termeni in (27). Cu același numar de termeni, se obțin
in coloana a patra 8 zecimale exacte in R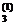 . Insumand
. Insumand 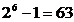 termeni in
termeni in 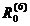 , in
, in 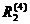 se obțin 11 zecimale exacte.
se obțin 11 zecimale exacte.
Acest
exemplu este ilustrativ pentru puterea de accelerare a algoritmului lui
Richardson (formula (27) este obținuta din formula trapezelor).


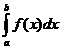 =
=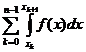 .
.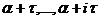
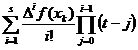
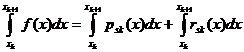 .
.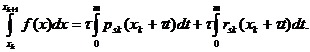
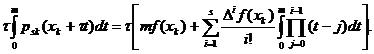
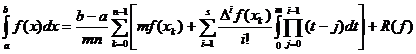 ,
,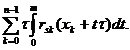
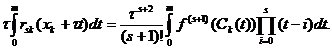
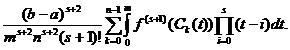
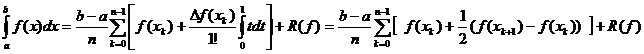
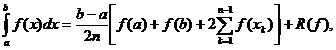
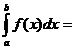
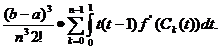
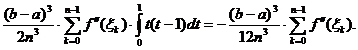
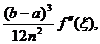
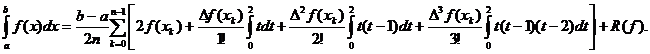 Ultima integrala are valoarea zero. Apoi:
Ultima integrala are valoarea zero. Apoi: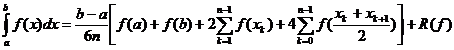

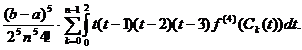
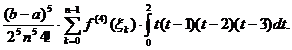
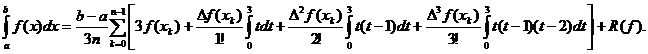
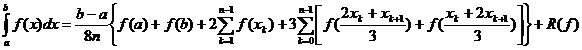
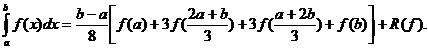
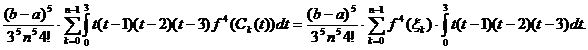
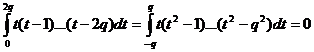 ,
,