Teorema de structura a multimii caracteristice pentru
operatori T= I-U cu U compact
compact
Teorema asupra multimii
caracteristice a unui operator compact se extinde la operatorii de forma considerata
in teorema anterioara . Anume are loc
Teorema IV.3.1. Daca
pentru un m oarecare operatorul  este compact atunci
este compact atunci
1)
multimea caracteristica  a operatorului U consta numai din valori
caracteristice iar fiecare valoare caracteristica are rang finit si subspatiul propriu
corespunzator este finit dimensional ; 2) in fiecare disc
a operatorului U consta numai din valori
caracteristice iar fiecare valoare caracteristica are rang finit si subspatiul propriu
corespunzator este finit dimensional ; 2) in fiecare disc  al planului complex se afla numai un numar finit de
valori caracteristice
al planului complex se afla numai un numar finit de
valori caracteristice
Demonstratie. Tinand seama de rezultatul lemei IV.2.2 ne putem limita la
demonstrarea primului punct al teoremei. In plus prima
parte rezulta in mod evident din teorema IV.2.3. Prin
urmare ramane de demonstrat doar finitudinea dimensiunii subspatiului
propriu corespunzator.
Fara a se restrange generalitatea se
poate presupune ca valoarea proprie considerata este  Pe baza dezvoltarii (18) se poate scrie
Pe baza dezvoltarii (18) se poate scrie

Deoarece operatorii 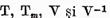 comuta intrei ei avem
comuta intrei ei avem
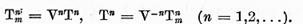
De aici rezulta ca

Astfel deoarece 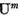 este operator compact si tinand
seama ca pentru astfel de operatori afirmatia a fost deja stabilita putem
conchide pe baza relatiei (19) ca aceasta afirmatie este
valabila si in cazul considerat.
este operator compact si tinand
seama ca pentru astfel de operatori afirmatia a fost deja stabilita putem
conchide pe baza relatiei (19) ca aceasta afirmatie este
valabila si in cazul considerat.
In incheiere sa
dam un exemplu de operator liniar continuu U care nu este compact dar 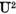 este compact.
este compact.
Fie X unul din spatiile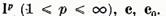 Pentru
Pentru  sa punem
sa punem 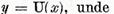
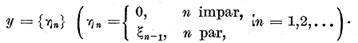
Evident 
Observatie. Intrucat
teoremele din capitolul III demonstrate pentru operatorii compacti, au
folosit doar acele proprietati ale operatorilor compacti care
sunt incluse in teorema I.2.1. si teorema III.2.1.
iar acele teoreme se extind fara modificare
la cazul operatorilor de forma considerata mai sus, rezultatele mentionate
sunt de asemenea adevarate daca se presupune doar ca o
anumita putere a operatorului U
este compacta.

