TRIGONOMETRIE
1. FUNCTIA TRIGONOMETRICǍ
Functia trigonometricǎ intr-un cerc cu razǎ 1 exprimǎ relatia de determinare a
coordonatelor punctelor de pe cerc,cat si de pe perpendiculara dusǎ la raza cercului
la o rotatie a punctului cu 360s in jurul centrului de cerc ( vezi fig. 1).
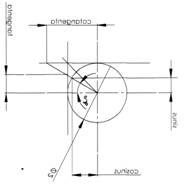
Relatii intre functiile trigonometrice
sinus,cosin,
tangentǎ si
cotangantǎ in
cercul de razǎ 1 :
a) sin ² + cos
² = 1 ;
sin
α 1s
b) tg α=-------
; cotg α = ------ ;
cos
α tg α
1 1
c) sec α=------;
cosec α = -------- .
cos α sin α
Fig. 1
NOTǍ :Unghiul α se exprima in grade sau radiani .Unghiul de un radian este
unghiul care desfǎsoarǎ un arc de cerc de lungime egalǎ cu raza.
Formula de
transformare radiani in grade sexagesimale este :
π 180s
------- == ------
α αs
EXEMPLU 1. Sǎ se determine valoarea unghiului in grade sexagesimale
corespunzǎtor unghiului de un radian : Aplicand formula
obtinem expresia :
3,14 180s
------------- = ----- ----- ------ ;
αs
αs = 180 s · 1/3.14 = 57s 19′ 12″ .
APLICATIE :Determinarea arcului de cerc la un
cerc cu diametru d cǎreia ii
corespunde unghiul αs la centru :
Aplicand regula de trei simplǎ raportatǎ la lungimea cercului se determinǎ
formula de calcul pentru determunarea arcului de cerc :
L ( π.d
) . . . . . . . .. 360s unde L→
lungimea
x . . . . . . . αs cercului.
-------- ----- ------ ----- ----- ---------- x→lungime
arc.
x = L · αs /360s = π · d · αs/360s.
DETERMINAREA VALORILOR FUNCTIILOR
TRIGONOMETRICE CU AJUTORUL TABELULUI
INTR-UN TRIUNGHI DREPTUNGHIC
Triunghiul dreptunghic are un unghi de 90s, un unghi ascutit s
<90s si un unghi optuz s > 90s , care se aflǎ in relatia αs + βs = 90s; de asemenea are o laturǎ
opusǎ unghiului de 90s, care se chiamǎ ipotenuzǎ si douǎ laturi ce se opun unghiu-
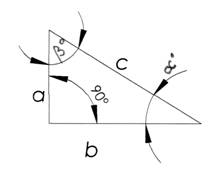 lui αs si unghiului βs ce se numesc catete ( Fig. ).
lui αs si unghiului βs ce se numesc catete ( Fig. ).
- unde : a-
catetǎ ;
b-
catetǎ ; c- ipotenuza
;
αs-unghi ascutit ;
βs-unghi opuz ;
γs-unghi drept = 90s.
Fig. 2
RELATIILE FUNCTIILOR TRIGONOMETRICE IN TRIUNGHIUL DE MAI
SUS:
a b
I) sinαs = -------- ; V) sin βs = --------- ; IX) a = c·sin αs ; XIII) b =c·sinβs;
c c
b a
II) cosαs = -------- ; VI) cos βs = --------- ; X) b = c·cos αs ; XIV) a=c·cosβs ;
c c
a b
III) tg αs = -------- ; VII) tg βs = --------- ; XI) a = b· tg αs ; XV)
b=a·tg βs ;
b a
b a
IV) ctg αs = -------- ; VIII) ctg βs = --------- ;XII) b =
a·ctg αs ; XVI) a=b·ctgβs ;
a b
a b b a a a
XVII) c =----------- = --------- = --------- = --------- ; XVIII) b = -------- = ---------- ;
sin αs sin
βs cos αs cos βs tg αs ctg βs
b b
XIX) a =--------- = ---------- .
tg βs ctg
αs
3. TABEL CU VALOAREA FUNCTIILOR TRIGONOMETRICE
sin, cos, tg, ctg -grade sexagesimale
|
SINUS 0s - 45s
|
|
GRAD ↓ 0′ 10′ 20′ 30′ 40′ 50′ 60′ ----
|
|
0
|
0,0000
|
0,0029
|
0,0058
|
0,0087
|
0,0116
|
0,0145
|
0,0175
|
89
|
|
1
|
0,0175
|
0,0204
|
0,0233
|
0,0262
|
0,0291
|
0,0320
|
0,0349
|
88
|
|
2
|
0,0349
|
0,0378
|
0,0407
|
0,0436
|
0,0465
|
0,0494
|
0,0523
|
87
|
|
3
|
0,0523
|
0,0552
|
0,0581
|
0,0610
|
0,0640
|
0,0669
|
0,0698
|
86
|
|
4
|
0,0698
|
0,0727
|
0,0756
|
0,0785
|
0,0814
|
0,0843
|
0,0872
|
85
|
|
5
|
0,0872
|
0,0901
|
0,0929
|
0,0958
|
0,0987
|
0,1016
|
0,1045
|
84
|
|
6
|
0,1045
|
0,1074
|
0,1103
|
0,1132
|
0,1161
|
0,1190
|
0,1219
|
83
|
|
7
|
0,1219
|
0,1248
|
0,1276
|
0,1305
|
0,1334
|
0,1363
|
0,1392
|
82
|
|
8
|
0,1392
|
0,1421
|
0,1449
|
0,1478
|
0,1507
|
0,1536
|
0,1564
|
81
|
|
9
|
0,1564
|
0,1593
|
0,1622
|
0,1650
|
0,1679
|
0,1708
|
0,1736
|
80
|
|
10
|
0,1736
|
0,1765
|
0,1794
|
0,1822
|
0,1851
|
0,1880
|
0,1908
|
79
|
|
11
|
0,1908
|
0,1937
|
0,1965
|
0,1994
|
0,2022
|
0,2051
|
0,2079
|
78
|
|
12
|
0,2079
|
0,2108
|
0,2136
|
0,2164
|
0,2193
|
0,2221
|
0,2250
|
77
|
|
13
|
0,2250
|
0,2278
|
0,2306
|
0,2334
|
0,2363
|
0,2391
|
0,2419
|
76
|
|
14
|
0,2419
|
0,2447
|
0,2476
|
0,2504
|
0,2532
|
0,2560
|
0,2588
|
75
|
|
15
|
0,2588
|
0,2616
|
0,2644
|
0,2672
|
0,2700
|
0,2728
|
0,2756
|
74
|
|
16
|
0,2756
|
0,2784
|
0,2812
|
0,2840
|
0,2868
|
0,2896
|
0,2924
|
73
|
|
17
|
0,2924
|
0,2952
|
0,2979
|
0,3007
|
0,3035
|
0,3062
|
0,3090
|
72
|
|
18
|
0,3090
|
0,3118
|
0,3145
|
0,3173
|
0,3201
|
0,3228
|
0,3256
|
71
|
|
19
|
0,3256
|
0,3283
|
0,3311
|
0,3338
|
0,3365
|
0,3393
|
0,3420
|
70
|
|
20
|
0,3420
|
0,3448
|
0,3475
|
0,3502
|
0,3529
|
0,3557
|
0,3584
|
69
|
|
21
|
0,3584
|
0,3611
|
0,3638
|
0,3665
|
0,3692
|
0,3719
|
0,3746
|
68
|
|
22
|
0,3746
|
0,3773
|
0,3800
|
0,3827
|
0,3854
|
0,3881
|
0,3907
|
67
|
|
23
|
0,3907
|
0,3934
|
0,3961
|
0,3987
|
0,4014
|
0,4041
|
0,4067
|
66
|
|
24
|
0,4067
|
0,4094
|
0,4120
|
0,4147
|
0,4173
|
0,4200
|
0,4226
|
65
|
|
25
|
0,4226
|
0,4253
|
0,4279
|
0,4305
|
0,4331
|
0,4358
|
0,4384
|
64
|
|
26
|
0,4384
|
0,4410
|
0,4436
|
0,4462
|
0,4488
|
0,4514
|
0,4540
|
63
|
|
27
|
0,4540
|
0,4566
|
0,4592
|
0,4617
|
0,4643
|
0,4669
|
0,4695
|
62
|
|
28
|
0,4695
|
0,4720
|
0,4746
|
0,4772
|
0,4797
|
0,4823
|
0,4848
|
61
|
|
29
|
0,4848
|
0,4874
|
0,4899
|
0,4924
|
0,4950
|
0,4975
|
0,5000
|
60
|
|
30
|
0,5000
|
0,5025
|
0,5050
|
0,5075
|
0,5100
|
0,5125
|
0,5150
|
59
|
|
31
|
0,5150
|
0,5175
|
0,5200
|
0,5225
|
0,5250
|
0,5275
|
0,5299
|
58
|
|
32
|
0,5299
|
0,5324
|
0,5348
|
0,5373
|
0,5398
|
0,5422
|
0,5446
|
57
|
|
33
|
0,5446
|
0,5471
|
0,5495
|
0,5519
|
0,5544
|
0,5568
|
0,5592
|
56
|
|
34
|
0,5592
|
0,5616
|
0,5640
|
0,5664
|
0,5688
|
0,5712
|
0,5736
|
55
|
|
35
|
0,5736
|
0,5760
|
0,5783
|
0,5807
|
0,5831
|
0,5854
|
0,5878
|
54
|
|
36
|
0,5878
|
0,5901
|
0,5925
|
0,5948
|
0,5972
|
0,5995
|
0,6018
|
53
|
|
37
|
0,6018
|
0,6041
|
0,6065
|
0,6088
|
0,6111
|
0,6134
|
0,6157
|
52
|
|
38
|
0,6157
|
0,6180
|
0,6202
|
0,6225
|
0,6248
|
0,6271
|
0,6293
|
51
|
|
39
|
0,6293
|
0,6316
|
0,6338
|
0,6361
|
0,6383
|
0,6406
|
0,6428
|
50
|
|
40
|
0,6428
|
0,6450
|
0,6472
|
0,6494
|
0,6517
|
0,6539
|
0,6561
|
49
|
|
41
|
0,6561
|
0,6583
|
0,6604
|
0,6626
|
0,6648
|
0,6670
|
0,6691
|
48
|
|
42
|
0,6691
|
0,6713
|
0,6734
|
0,6756
|
0,6777
|
0,6799
|
0,6820
|
47
|
|
43
|
0,6820
|
0,6841
|
0,6862
|
0,6884
|
0,6905
|
0,6926
|
0,6947
|
46
|
|
44
|
0,6947
|
0,6967
|
0,6988
|
0,7009
|
0,7030
|
0,7050
|
0,7071
|
45
|
|
-- --- 60′ 50′ 40′ 30′ 20′ 10′ 0′ GRAD
↑
|
|
COSINUS 45s - 90s
|
8
SINUS 45s- 90s
|
|
GRAD↓ 0′ 10′ 20′ 30′ 40′ 50′ 60′ -----
|
|
|
45
|
0,7071
|
0,7092
|
0,7112
|
0,7133
|
0,7153
|
0,7173
|
0,7193
|
44
|
|
|
46
|
0,7193
|
0,7214
|
0,7234
|
0,7245
|
0,7274
|
0,7294
|
0,7314
|
43
|
|
|
47
|
0,7314
|
0,7333
|
0,7353
|
0,7373
|
0,7392
|
0,7412
|
0,7431
|
42
|
|
|
48
|
0,7431
|
0,7451
|
0,7470
|
0,7490
|
0,7509
|
0,7528
|
0,7547
|
41
|
|
|
49
|
0,7547
|
0,7566
|
0,7585
|
0,7604
|
0,7623
|
0,7642
|
0,7660
|
40
|
|
|
50
|
0,7660
|
0,7679
|
0,7698
|
0,7716
|
0,7735
|
0,7753
|
0,7771
|
39
|
|
|
51
|
0,7771
|
0,7790
|
0,7808
|
0,7826
|
0,7844
|
0,7862
|
0,7880
|
38
|
|
|
52
|
0,7880
|
0,7898
|
0,7916
|
0,7934
|
0,7951
|
0,7969
|
0,7986
|
37
|
|
|
53
|
0,7986
|
0,8004
|
0,8021
|
0,8039
|
0,8056
|
0,8073
|
0,8090
|
36
|
|
|
54
|
0,8090
|
0,8107
|
0,8124
|
0,8141
|
0,8158
|
0,8175
|
0,8192
|
35
|
|
|
55
|
0,8192
|
0,8208
|
0,8225
|
0,8241
|
0,8258/
|
0,8274
|
0,8290
|
34
|
|
|
56
|
0,8290
|
0,8307
|
0,8323
|
0,8339
|
0,8355
|
0,8371
|
0,8387
|
33
|
|
|
57
|
0,8387
|
0,8403
|
0,8418
|
0,8434
|
0,8450
|
0,8465
|
0,8480
|
32
|
|
|
58
|
0,8480
|
0,8496
|
0,8511
|
0,8526
|
0,8542
|
0,8557
|
0,8572
|
31
|
|
|
59
|
0,8572
|
0,8587
|
0,8601
|
0,8616
|
0,8631
|
0,8646
|
0,8660
|
30
|
|
|
60
|
0,8660
|
0,8675
|
0,8689
|
0,8704
|
0,8718
|
0,8732
|
0,8746
|
29
|
|
|
61
|
0,8746
|
0,8760
|
0,8774
|
0,8788
|
0,8802
|
0,8816
|
0,8829
|
28
|
|
|
62
|
0,8829
|
0,8843
|
0,8857
|
0,8870
|
0,8884
|
0,8897
|
0,8910
|
27
|
|
|
63
|
0,8910
|
0,8923
|
0,8936
|
0,8949
|
0,8962
|
0,8975
|
0,8988
|
26
|
|
|
64
|
0,8988
|
0,9001
|
0,9013
|
0,9026
|
0,9038
|
09051
|
0,9063
|
25
|
|
|
65
|
0,9063
|
0,9075
|
0,9088
|
0,9100
|
0,9112
|
0,9124
|
0,9135
|
24
|
|
|
66
|
0,9135
|
0,9147
|
0,9159
|
0,9171
|
0,9182
|
0,9194
|
0,9205
|
23
|
|
|
67
|
0,9205
|
0,9216
|
0,9228
|
0,9239
|
0,9250
|
0,9261
|
0,9272
|
22
|
|
|
68
|
0,9272
|
0,9283
|
0,9293
|
0,9304
|
0,9315
|
0,9325
|
0,9336
|
21
|
|
|
69
|
0,9336
|
0,9346
|
0,9356
|
0,9367
|
0,9377
|
0,9387
|
0,9397
|
20
|
|
|
70
|
0,9397
|
0,9407
|
0,9417
|
0,9426
|
0,9436
|
0,9446
|
0,9455
|
19
|
|
|
71
|
0,9455
|
0,9465
|
0,9474
|
0,9483
|
0,9492
|
0,9502
|
0,9511
|
18
|
|
|
72
|
0,9511
|
0,9520
|
0,9528
|
0,9537
|
0,9546
|
0,9555
|
0,9563
|
17
|
|
|
73
|
0,9563
|
0,9572
|
0,9580
|
0,9588
|
0,9596
|
0,9605
|
0,9613
|
16
|
|
|
74
|
0,9613
|
0,9621
|
0,9628
|
0,9636
|
0,9644
|
0,9652
|
0,9659
|
15
|
|
|
75
|
0,9659
|
0,9667
|
0,9674
|
0,9681
|
0,9689
|
0,9696
|
0,9703
|
14
|
|
|
76
|
0,9703
|
0,9710
|
0,9717
|
0,9724
|
0,9730
|
0,9737
|
0,9744
|
13
|
|
|
77
|
0,9744
|
0,9750
|
0,9757
|
0,9763
|
0,9769
|
0,9775
|
0,9781
|
12
|
|
|
78
|
0,9781
|
0,9787
|
0,9793
|
0,9799
|
0,9805
|
0,9811
|
0,9816
|
11
|
|
|
79
|
0,9816
|
0,9822
|
0,9827
|
0,9833
|
0,9838
|
0,9843
|
0,9848
|
10
|
|
|
80
|
0,9848
|
0,9853
|
0,9858
|
0,9863
|
0,9868
|
0,9872
|
0,9877
|
9
|
|
|
81
|
0,9877
|
0,9881
|
0,9886
|
0,9890
|
0,9894
|
0,9899
|
0,9903
|
8
|
|
|
82
|
0,9903
|
0,9907
|
0,9911
|
0,9914
|
0,9918
|
0,9922
|
0,9925
|
7
|
|
|
83
|
0,9925
|
0,9929
|
0,9932
|
0,9936
|
0,9939
|
0,9942
|
0,9945
|
6
|
|
|
84
|
0,9945
|
0,9948
|
0,9951
|
0,9954
|
0,9957
|
0,9959
|
0,9962
|
5
|
|
|
85
|
0,9962
|
0,9964
|
0,9967
|
0,9969
|
0,9971
|
0,9974
|
0,9976
|
4
|
|
|
86
|
0,9976
|
0,9978
|
0,9980
|
0,9981
|
0,9983
|
0,9985
|
0,9986
|
3
|
|
|
87
|
0,9986
|
0,9988
|
0,9989
|
0,9990
|
0,9992
|
0,9993
|
0,9994
|
2
|
|
|
88
|
0,9994
|
0,9995
|
0,9996
|
0,9997
|
0,99975
|
0,9998
|
0,99985
|
1
|
|
|
89
|
0,99985
|
0,99989
|
0,99993
|
0,99996
|
0,99998
|
0,99999
|
1,0000
|
0
|
|
|
-------- 60′ 50′ 40′ 30′ 20′ 10′ 0′ GRAD
↑
|
|
COSINUS 0s - 45s
|
TANGENTǍ 0s - 45s
|
GRAD ↓ 0′ 10′ 20′ 30′ 40′ 50′ 60′ --------
|
|
0s
|
0,0000
|
0,0029
|
0,0058
|
0,0087
|
0,0116
|
0,0145
|
0,0175
|
89
|
|
1
|
0,0175
|
0,0204
|
0,0233
|
0,0262
|
0,0291
|
0,0320
|
0,0349
|
88
|
|
2
|
0,0349
|
0,0378
|
0,0407
|
0,0437
|
0,0466
|
0,0495
|
0,0524
|
87
|
|
3
|
0,0524
|
0,0553
|
0,0582
|
0,0612
|
0,0641
|
0,0670
|
0,0699
|
86
|
|
4
|
0,0699
|
0,0729
|
0,0758
|
0,0787
|
0,0816
|
0,0846
|
0,0875
|
85
|
|
5
|
0,0875
|
0,0904
|
0,0934
|
0,0963
|
0,0992
|
0,1022
|
0,1051
|
84
|
|
6
|
0,1051
|
0,1080
|
0,1110
|
0,1139
|
0,1169
|
0,1198
|
0,1228
|
83
|
|
7
|
0,1228
|
0,1257
|
0,1287
|
0,1317
|
0,1346
|
0,1376
|
0,1405
|
82
|
|
8
|
0,1405
|
0,1435
|
0,1465
|
0,1495
|
0,1524
|
0,1554
|
0,1584
|
81
|
|
9
|
0,1584
|
0,1614
|
0,1644
|
0,1673
|
0,1703
|
0,1733
|
0,1763
|
80
|
|
10
|
0,1763
|
0,1793
|
0,1823
|
0,1853
|
0,1883
|
0,1914
|
0,1944
|
79
|
|
11
|
0,1944
|
0,1974
|
0,2004
|
0,2035
|
0,2065
|
0,2095
|
0,2126
|
78
|
|
12
|
0,2126
|
0,2156
|
0,2186
|
0,2217
|
0,2247
|
0,2278
|
0,2309
|
77
|
|
13
|
0,2309
|
0,2339
|
0,2370
|
0,2401
|
0,2432
|
0,2462
|
0,2493
|
76
|
|
14
|
0,2493
|
0,2524
|
0,2555
|
0,2586
|
0,2617
|
0,2648
|
0,2679
|
75
|
|
15
|
0,2679
|
0,2711
|
0,2742
|
0,2773
|
0,2805
|
0,2836
|
0,2867
|
74
|
|
16
|
0,2867
|
0,2899
|
0,2931
|
0,2962
|
0,2994
|
0,3026
|
0,3057
|
73
|
|
17
|
0,3057
|
0,3089
|
0,3121
|
0,3153
|
0,3185
|
0,3217
|
0,3249
|
72
|
|
18
|
0,3249
|
0,3281
|
0,3314
|
0,3346
|
0,3378
|
0,3411
|
03443
|
71
|
|
19
|
0,3443
|
0,3476
|
0,3508
|
0,3541
|
0,3574
|
0,3607
|
0,3640
|
70
|
|
20
|
0,3640
|
0,3673
|
0,3706
|
0,3739
|
0,3772
|
0,3805
|
0,3839
|
69
|
|
21
|
0,3839
|
0,3872
|
0,3906
|
0,3939
|
0,3973
|
0,4006
|
0,4040
|
68
|
|
22
|
0,4040
|
0,4074
|
0,4108
|
0,4142
|
0,4176
|
0,4210
|
0,4245
|
67
|
|
23
|
0,4245
|
0,4279
|
0,4314
|
0,4348
|
0,4383
|
0,4417
|
0,4452
|
66
|
|
24
|
0,4452
|
0,4487
|
0,4522
|
0,4557
|
0,4592
|
0,4628
|
0,4663
|
65
|
|
25
|
0,4663
|
0,4699
|
0,4734
|
0,4770
|
0,4806
|
0,4841
|
0,4877
|
64
|
|
26
|
0,4877
|
0,4913
|
0,4950
|
0,4986
|
0,5022
|
0,5059
|
0,5095
|
63
|
|
27
|
0,5095
|
0,5132
|
0,5169
|
0,5206
|
0,5243
|
0,5280
|
0,5317
|
62
|
|
28
|
0,5317
|
0,5354
|
0,5392
|
0,5430
|
0,5467
|
0,5505
|
0,5543
|
61
|
|
29
|
0,5543
|
0,5581
|
0,5619
|
0,5658
|
0,5696
|
0,5735
|
0,5774
|
60
|
|
30
|
0,5774
|
0,5812
|
0,5851
|
0,5890
|
0,5930
|
0,5969
|
0,6009
|
59
|
|
31
|
0,6009
|
0,6048
|
0,6088
|
0,6128
|
0,6168
|
0,6208
|
0,6249
|
58
|
|
32
|
0,6249
|
0,6289
|
0,6330
|
0,6371
|
0,6412
|
0,6453
|
0,6494
|
57
|
|
33
|
0,6494
|
0,6536
|
0,6577
|
0,6619
|
0,6661
|
0,6703
|
0,6745
|
56
|
|
34
|
0,6745
|
0,3787
|
0,6830
|
0,6873
|
0,6916
|
0,6959
|
0,7002
|
55
|
|
35
|
0,7002
|
0,7046
|
0,7089
|
0,7133
|
0,7177
|
0,7221
|
0,7265
|
54
|
|
36
|
0,7265
|
0,7310
|
0,7355
|
0,7400
|
0,7445
|
0,7490
|
0,7536
|
53
|
|
37
|
0,7536
|
0,7581
|
0,7627
|
0,7673
|
0,7720
|
0,7766
|
0,7813
|
52
|
|
38
|
0,7813
|
0,7860
|
0,7907
|
0,7954
|
0,8002
|
0,8050
|
0,8098
|
51
|
|
39
|
0,8098
|
0,8146
|
0,8195
|
0,8243
|
0,8292
|
0,8342
|
0,8391
|
50
|
|
40
|
0,8391
|
0,8441
|
0,8491
|
0,8541
|
0,8591
|
0,8642
|
0,8693
|
49
|
|
41
|
0,8693
|
0,8744
|
0,8796
|
0,8847
|
0,8899
|
0,8952
|
0,9004
|
48
|
|
42
|
0,9004
|
0,9057
|
0,9110
|
0,9163
|
0,9217
|
0,9271
|
0,9325
|
47
|
|
43
|
0,9325
|
0,9380
|
0,9435
|
0,9490
|
0,9545
|
0,9601
|
0,9657
|
46
|
|
44
|
0,9657
|
0,9713
|
0,9770
|
0,9827
|
0,9884
|
0,9942
|
1,0000
|
45s
|
|
-------- 60′ 50′ 40′ 30′ 20′ 10′ 0′ GRAD
↑
|
COTANGENTǍ 45s - 90s
|
TANGENTǍ 45s - 90s
|
GRAD ↓ 0′ 10′ 20′ 30′ 40′ 50′ 60′ ------
|
|
45s
|
1,0000
|
1,0058
|
1,0117
|
1,0176
|
1,0235
|
1,0295
|
1,0355
|
44
|
|
46
|
1,0355
|
1,0416
|
1,0477
|
1,0538
|
1,0599
|
1,0661
|
1,0724
|
43
|
|
47
|
1,0724
|
1,0786
|
1,0850
|
1,0913
|
1,0977
|
1,1041
|
1,1106
|
42
|
|
48
|
1,1106
|
1,1171
|
1,1237
|
1,1303
|
1,1369
|
1,1436
|
1,1504
|
41
|
|
49
|
1,1504
|
1,1571
|
1,1640
|
1,1708
|
1,1778
|
1,1847
|
1,1918
|
40
|
|
50
|
1,1918
|
1,1988
|
1,2059
|
1,2131
|
1,2203
|
1,2276
|
1,2349
|
39
|
|
51
|
1,2349
|
1,2423
|
1,2497
|
1,2572
|
1,2647
|
1,2723
|
1,2799
|
38
|
|
52
|
1,2799
|
1,2876
|
1,2954
|
1,3032
|
1,3111
|
1,3190
|
1,3270
|
37
|
|
53
|
1,3270
|
1,3351
|
1,3432
|
1,3514
|
1,3597
|
1,3680
|
1,3764
|
36
|
|
54
|
1,3764
|
1,3848
|
1,3934
|
1,4019
|
1,4106
|
1,4193
|
1,4281
|
35
|
|
55
|
1,4281
|
1,4370
|
1,4460
|
1,4550
|
1,4641
|
1,4733
|
1,4826
|
34
|
|
56
|
1,4826
|
1,4919
|
1,5013
|
1,5108
|
1,5204
|
1,5301
|
1,5399
|
33
|
|
57
|
1,5399
|
1,5497
|
1,5597
|
1,5697
|
1,5798
|
1,5900
|
1,6003
|
32
|
|
58
|
1,6003
|
1,6107
|
1,6213
|
1,6318
|
1,6426
|
1,6534
|
1,6643
|
31
|
|
59
|
1,6643
|
1,6753
|
1,6864
|
1,6977
|
1,7090
|
1,7205
|
1,7321
|
30
|
|
60
|
1,7321
|
1,7438
|
1,7556
|
1,7675
|
1,7796
|
1,7917
|
1,8041
|
29
|
|
61
|
1,8041
|
1,8165
|
1,8291
|
1,8418
|
1,8546
|
1,8676
|
1,8807
|
28
|
|
62
|
1,8807
|
1,8940
|
1,9074
|
1,9210
|
1,9347
|
1,9486
|
1,9626
|
27
|
|
63
|
1,9626
|
1,9768
|
1,9912
|
2,0057
|
2,0204
|
2,0353
|
2,0503
|
26
|
|
64
|
2,0503
|
2,0655
|
2,0809
|
2,0965
|
2,1123
|
2,1283
|
2,1445
|
25
|
|
65
|
2,1445
|
2,1609
|
2,1775
|
2,1943
|
2,2113
|
2,2286
|
2,2460
|
24
|
|
66
|
2,2460
|
2,2637
|
2,2817
|
2,2998
|
2,3183
|
2,3369
|
2,3559
|
23
|
|
67
|
2,3559
|
2,3750
|
2,3945
|
2,4142
|
2,4342
|
2,4545
|
2,4751
|
22
|
|
68
|
2,4751
|
2,4960
|
2,5172
|
2,5387
|
2,5605
|
2,5826
|
2,6051
|
21
|
|
69
|
2,6051
|
2,6279
|
2,6511
|
2,6746
|
2,6985
|
2,7228
|
2,7475
|
20
|
|
70
|
2,7475
|
2,7725
|
2,7980
|
2,8239
|
2,8502
|
2,8770
|
2,9042
|
19
|
|
71
|
2,9042
|
2,9319
|
2,9600
|
2,9887
|
3,0178
|
3,0475
|
3,0777
|
18
|
|
72
|
3,0777
|
3,1084
|
3,1397
|
3,1716
|
3,2041
|
3,2371
|
3,2709
|
17
|
|
73
|
3,2709
|
3,3052
|
3,3402
|
3,3759
|
3,4124
|
3,.4495
|
3,4874
|
16
|
|
74
|
3,4874
|
3,5261
|
3,5656
|
3,6059
|
3,6470
|
3,6891
|
3,7321
|
15
|
|
75
|
3,7321
|
3,7760
|
3,8208
|
3,8667
|
3,9136
|
3,9617
|
4,0108
|
14
|
|
76
|
4,0108
|
4,0611
|
4,1126
|
4,1653
|
4,2193
|
4,2747
|
4,3315
|
13
|
|
77
|
4,3315
|
4,3897
|
4,4494
|
4,5107
|
4,5736
|
4,6383
|
4,7046
|
12
|
|
78
|
4,7046
|
4,7729
|
4,8430
|
4,9152
|
4,9894
|
5,0658
|
5,1446
|
11
|
|
79
|
5,1446
|
5,2257
|
5,3093
|
5,3955
|
5,4845
|
5,5764
|
5,6713
|
10
|
|
80
|
5,6713
|
5,7694
|
5,8708
|
5,9758
|
6,0844
|
6,1970
|
6,3138
|
9
|
|
81
|
6,3138
|
6,4348
|
6,5605
|
6,6912
|
6,8269
|
6,9682
|
7,1154
|
8
|
|
82
|
7,1154
|
7,2687
|
7,4287
|
7,5958
|
7,7704
|
7,9530
|
8,1444
|
7
|
|
83
|
8,1444
|
8,3450
|
8,5556
|
8,7769
|
9,0098
|
9,2553
|
9,5144
|
6
|
|
84
|
9,5144
|
9,7882
|
10,0780
|
10,3854
|
10,7119
|
11,0594
|
11,4301
|
5
|
|
85
|
11,4301
|
11,8262
|
12,2505
|
12,7062
|
13,1969
|
13,7267
|
14,3007
|
4
|
|
86
|
14,3007
|
14,9244
|
15,6048
|
16,3499
|
17,1693
|
18,0750
|
19,0811
|
3
|
|
87
|
19,0811
|
20,2056
|
21,4704
|
22,9038
|
24,5418
|
26,4316
|
28,6363
|
2
|
|
88
|
28,6363
|
31,2416
|
34,3678
|
38,1885
|
42,9641
|
49,1039
|
57,2900
|
1
|
|
89
|
57,2900
|
68,7501
|
85,9398
|
|
|
|
∞
|
0s
|
|
--------- 60′ 50′ 40′ 30′ 20′ 10′ 0′ GRAD
↑
|
COTANGENTǍ 0s - 45s
|
4. APLICATII
EXEMPLU 1. Sǎ se determine valoatrea functiilor trigonometrice sin , cos , tg
,ctg la urmǎtoarele unghiuri :
α = 5s 30′ ;16s ;25s 20′ ;30s si 45s 50′. Folosind cele patru
tabele astfel :
In dreptul fiecǎrui rand corespunzǎtor gradelor si in dreptul fiecǎrei
coloane corespunzǎtor minutelor aflǎm valoarea functiilor sin , cos , tg , ctg :
sin 5s 30′ =
0,0958 ; cos 5s 30′ = 0,9954 ; tg 5s 30′ = 0,0963 ; ctg 5s 30′ = 10,3854 ;
sin16s 0′ = 0,2588 ; cos16s 0′ = 0,9613 ; tg16s 0′ = 0,2867 ; ctg16s 0′ = 3,4874 ;
sin25s20′ =
0,4279 ; cos25s20′ = 0,9038 ; tg25s20′ = 0,4734 ; ctg25s20′ = 2,1123 ;
sin30s 0′ = 0,5000 ; cos30s 0′ = 0,8660 ; tg30s 0′ = 0,5774 ; ctg30s 0′ = 1,7321 ;
sin45s50′ =
0,7173 ; cos45s50′ = 0,6967 ; tg45s50′ = 1,0295 ; ctg45s50′ = 0,9713 .
EXEMPLU In triunghiu dreptunghic din fig. 2 se dǎ cateta b si unghiul alǎturat
αs (b = 40 mm ,αs=
20s) si se cere determinarea catetei a si ipotenuza c .
1. Pentru determinarea catetei a se aplicǎ formula XI :
a =b · tg αs → a = 40 · tg 20s = 40 · 0,3640 = 14,56. a= 14,56 mm.
Pentru determinarea ipotenuzei c se aplicǎ formula XVII :
a 14,56 14,56
c =---------- = -----------=------------ = 42,57 mm. c = 42,57 mm.
sin s sin 20s 0,3420
EXEMPLU 3.In triunghiul dreptunghic din fig. 2 se dǎ cateta a si ipotenuza c
( a = 15 mm ; c = 30 mm ) si se cere determinarea unghiurilor αs si βs.
1.Pentru determinarea unghiului αs se aplicǎ formula I si FUNCTIA
TRIGONOMETRICǍ INVERSǍ .
NOTǍ: FUNCTIA TRIGONOMETRICǍ INVERSǍ SE EXPRIMǍ ASTFEL :
UNGHI = ARC Fct.TRG.
VF. unde ARC.→expresia functiei
trigonome-
trice inversǎ;Fct.TRG. →functia trigonometricǎ( sin ,cos , tg , ctg
) si VF →valoarea
functiei trigonometrice , regǎsitǎ in tabelele cu valoarea functiilor trigonometrice .
a 15
sin αs
= --------- = --------- = 0,5000. αs = arc sin 0,5000 = 30s .
c 30
OBSERVATIE: Pentru determinarea unghiului cu ajutorul Functiei trigonometrice
inversǎ si a tabelului cu valoarea functiei trigonometrice respectivǎ
se procedeazǎ astfel: valoarea functiei rezultatǎ , respective valoarea
raportului celor douǎ laturi se cautǎ in tabelul cu valorile functiei
si pe pozitia care se aflǎ pe coloanǎ sunt minutele , iar pe orizon-
talǎ gradele : in cazul nostru pe coloanǎ se aflǎ 0′
si pe orizontalǎ
30s .
Pentru determinarea unghiului s se aplicǎ o propietate a triunghiu-
lui dreptunghic si anume suma celor douǎ unghiuri opuse catete-
lor este egalǎ cu 90s.
αs + βs = 90s ,
αs = 30s → 90s - 30s = 60s. βs = 60s.
EXEMPLU 4. Sǎ se determine unghiurile in grade sexagesimale,folosind
functia trigonometricǎ inversǎ si tabelele cu valorile functiilor
trigonometrice la urmǎtoarele valori: sin αs =0,0436 ;0,2221 ;
0,5000 ;0,6428 ;0,8660 ;0,9636 ;0,99999
- cos αs = 1,0000 ;0,9426 ;
0,8660 ;0,7193 ;0,7071 ;0,5000 ;0,0058 - tg αs = 0,0175 ;0,3640 ;
0,5774 ;1,0000 ;1,3764 ;6,3138 ;343,7737 -ctg αs = 57,2900 ;2,7475 ;
1,7321 ;1,0000 ;0,5774 ;0,1914 ;0,0000 :
αs = arcsin 0,0436 = 2s 30′ ; αs = arcsin 0,2221 = 12s 50′ ; αs = arcsin 0,5000 =30s 0′ ;
αs = arcsin 0,6428 = 40s 0′ ; αs = arcsin 0,8660 = 60s 0′ ; αs = arcsin 0,9636 =74s30′ ;
αs = arcsin0,99999= 89s 50′ .
s = arccos 1,0000 = 0s 0′ ; s
= arccos 0,9426 = 19s 30′ ; s = arccos0,8860 =30s 0′;
αs = arccos
0,7193 = 44s 0′ ; αs =
arccos 0,7071 = 45s 0′ ; αs = arccos0,5000 =60s 0′;
αs =
arccos 0,0058 = 89s 20′ .
αs = arctg 0,0175 = 1s 0′ ; αs = arctg 0,3640 = 19s 60′ ; αs = arctg 0,5774 =30s 0′;
αs = arctg 1,0000 =45s 0′ ; αs =
arctg 1,3764 = 54s 0′ ; αs = arctg 6,3138 =81s 0′;
αs = arctg343,7737= 89s 50′ .
αs =
arcctg57,2900 = 1s 0′ ; αs = arcctg 2,7475 = 20s 0′ ; αs = arcctg1,7321 =29s60′;
αs = arcctg 1,0000 =45s 0′ ; αs = arcctg 0,5774 = 60s 0′ ; αs = arcctg0,1914 =79s10′;
αs = arcctg 0,0000 = 89s 60′ =90s 0′ .
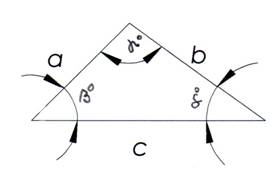
5. TRIUNGHI OARECARE
Triunghiul oarecare este triunghiul care are cele trei unghiuri diferite
ca valoare de 90s, iar suma lor este egalǎ cu 180s.
αs ; βs ; γs # 90s ;
αs + βs + γs = 180s.
RELATII DE CALCUL :
a b c
------ = --------- = --------- ;
sin s sin s sin s
b · sin
αs c · sin αs
a = --------- = ---------- ;
sin βs sin γs
a · sin βs c · sin βs
b = --------- = ---------- ;
sin αs sin γs
a · sin γs b · sin γs
c = --------- = ---------- . Fig . 3
sin αs sin βs
a² = b² + c² - 2·b·c·cos αs ; b² = a² + c² - 2· a· c · cosβs ;
c² = a² + b² - 2 ·
a · b · cos γs .
_____ _______ ______ ______
a = √ b² +c² - 2 ·
b · c · cos αs .