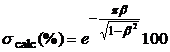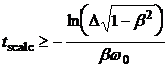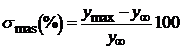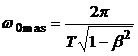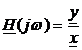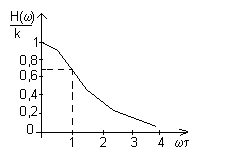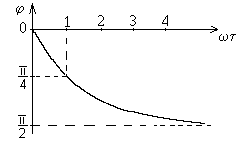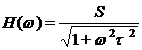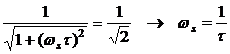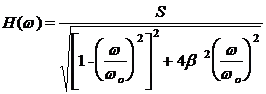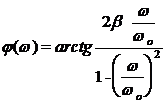CONVERTOARE DE MASURARE IN REGIM DINAMIC
1.Chestiuni de studiat.
Ecuatii de functionare pentru convertoarele de masurare.
1.2. Comportarea convertoarelor in domeniul
timp.
1.2.1.
Convertoare de ordinul I
1.2.2.
Convertoare de ordinul II
1.3.
Comportarea convertoarelor in domeniul frecventa.
Determinarea
experimentala a caracteristicii de frecventa
2.Mod de experimentare.
2.1.Regimul dinamic corespunde situatiei
in care marimea aplicata la intrarea unui mijloc de masurare
(MM) este functie de timp - x(t) - si ca urmare, si marimea
de iesire este functie de timp - y(t).
Cunoasterea comportarii in regim dinamic este importanta
atat pentru mijloacele de masurare a marimilor electrice si
neelectrice cat si pentru sistemele destinate vizualizari si masurarii
variatiei in timp a marimilor.
In procesul de masurare a unei marimi
variabile in timp MM prezinta o eroare dinamica datorata
structurii lantului de masurare si elementelor componente ale
convertoarelor de masurare. Variatiile marimii de intrare x(t)
nu pot fi urmarite instantaneu de catre MM datorita inertiilor
de tip electric, termic sau electromagnetic si a amortiza-rilor, iar evolutia in
timp a marimii de intrare se transmite cu intarziere la iesire,
uneori cu deformari in raport cu caracteristica statica de conversie.
Relatia
intre marimea de intrare si
cea de iesire este, in general, o ecuatie dife-rentiala
liniara cu coeficienti constanti, de ordin n:
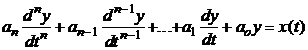
Functie de ordinul n al ecuatiei diferentiale,
convertoarele de masurare cele mai intalnite in structura lanturilor de masurare
se clasifica astfel:
-
convertoare de ordin zero 
-
convertoare de ordin I 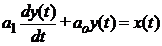
-
convertoare de ordin II 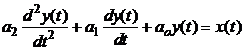
Analiza
comportarii in regim dinamic a unui mijloc de masurare se realizeaza
in domeniul timp si in domeniul frecventa.
Criteriile de apreciere a calitatii MM in
privinta comportarii in domeniul timp, in momentul aplicarii la
intrare a unei functii treapta sunt:
-
timpul de crestere - tcr - timpul in care semnalul creste
de la 10% la 90% din valoarea de regim stabilizat (fig.1)
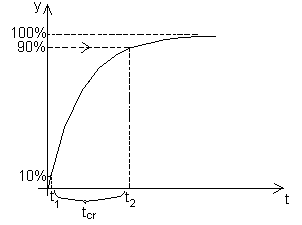
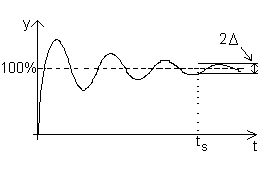
Fig.1. Definirea parametrilor
caracteristici in domeniul timp.
-
timpul de stabilizare -ts - timpul care trece de
la aplicarea marimi de intrare si pana cind marimea de iesire
atinge o valoare care se abate cu mai putin de o valoare prescrisa 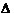 fata de cea
de regim stabilizat;
fata de cea
de regim stabilizat;
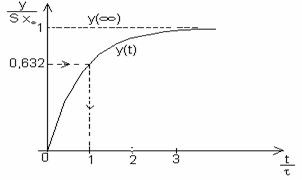
-constanta
de timp - -intervalul de timp dupa care semnalul de iesire
atinge 63,2% din valoarea de regim permanent;
-timpul
de intarziere - tm -decalajul de timp al raspunsului fata de intrare;
-supracresterea
- - depasirea
maxima a valorii de regim permanent a marimii de iesire, la
aplicarea functiei treapta la intrare.
2.2.1. Ecuatia de
functionare pentru convertorul de ordinul I se poate scrie si sub
forma:
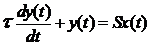
cu: - constanta de
timp, S-sensibilitatea convertorului.
Marimea
de iesire, la aplicarea unei functii treapta 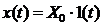 , are expresia:
, are expresia:
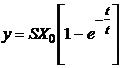
In
fig.2. se prezinta acest raspuns, sub forma adimensionala,
precum si modul de determinare a constantei de timp.
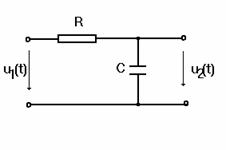
Se
va studia convertorul de ordinul I de tip
electric. Schema montajului utilizat este prezentata in fig.3.
|
Fig.3. Studiul
convertorului de ordinul I in domeniul timp
|
Ecuatia
specifica convertorului este : 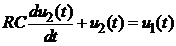
Se
aplica de la un generator de semnal tensiunea u (t) de forma dreptunghiulara cu durata mare a palierului. Se aduc cele
doua semnale la intrarile unui osciloscop cu doua canale. Se masoara
parametrii caracteristici (,
tcr , ts
Datele se trec in tabelul 2.
Tabel 2
|
R
|
C
|
calc = RC
|
mas
|
tcr
|
ts
|
|
F
|
s
|
s
|
s
|
s
|
|
|
|
|
|
|
Constanta de timp se determina in doua moduri:
direct din masurarea cu ajutorul osciloscopului ca fiind timpul in
care semnalul de iesire atinge 63,2 % din valoarea de regim;
prin calcul, functie de valorile masurate.
Pornind
de la:
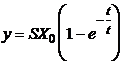
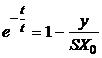
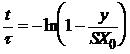
Din valorile masurate , la diferite intervale de
timp t , pentru y=u (t) si pentru SXo=u (t) se poate construi
graficul din fig.4.
|
Fig. 4. Mod de determinare a constantei de timp
|
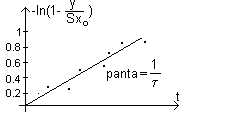
Prin regresie liniara se
construieste dreapta de aproximare cea mai probabila
y = ax + b
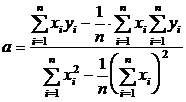
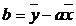
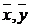 -valori medii
-valori medii
2.2.2.Ecuatia de functionare pentru
convertorul de ordinul II se poate pune
sub forma:
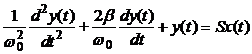
unde:
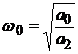 - pulsatia
proprie
- pulsatia
proprie 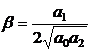 - factor de
amortizare
- factor de
amortizare
In
functie de valorile factorului de amortizare pot exista trei regimuri de functionare (fig.5):
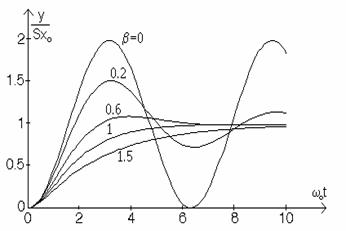
Fig.5. Raspunsurile
convertorului de ordinul II
-oscilator
amortizat
-aperiodic
critic
-aperiodic
supraamortizat
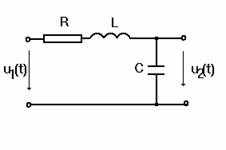
Se vor face masuratori pentru un convertor de ordinul II de tip
electric - fig.6
|
Fig.6.Schema de
montaj pentru convertorul de ordinul II de tip electric
|
Se
aplica de la un generator de semnal tensiunea u (t) de forma dreptunghiulara cu durata mare a palierului. Se aduc cele
doua semnale la intrarile unui osciloscop cu doua canale.
Datele se trec in tabelul 3.
Tabel 3
|
Regim
|
R
|
L
|
C
|
ocalc
|
calc
|
calc
|
tscalc
|
omas
|
mas
|
mas
|
tsmas
|
|
|
H
|
F
|
rad/s
|
|
|
s
|
rad/s
|
|
|
s
|
|
|
|
|
|
|
|
|
|
|
|
|
Valori calculate:

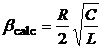
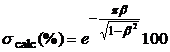
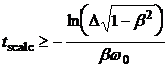 ( sau 0,05).
( sau 0,05).
Valori
masurate: 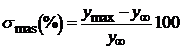
unde: ymax, y -valoarea maxima, respectiv de regim
permanent a marimii de iesire.

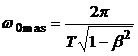 cu T -
perioada primei oscilatii
cu T -
perioada primei oscilatii
Comportarea in domeniul frecventa
se studiaza cu ajutorul caracteristicii de frecventa:
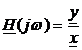
cu cele doua componente ale sale:
-
caracteristica amplitudine -frecventa 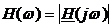
-
caracteristica faza - frecventa 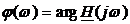
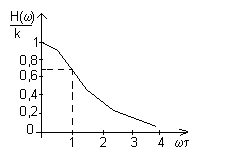
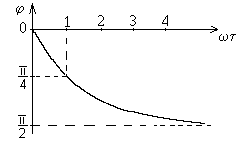
Fig.8.
Caracteristica de frecventa a convertorului de ordin I
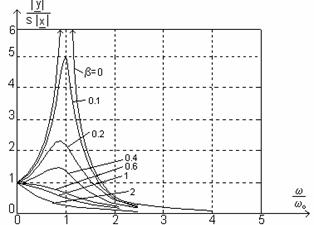
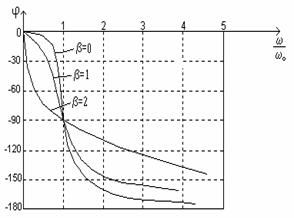
Fig.9.Caracteristica
de frecventa a convertorului de ordinul II
Se vor face
determinari pentru convertoarele de tip electric prezentate in fig.3 si
6. Se vor alimenta montajele, de la un
generator de semnal, cu tensiuni alternative sinusoidale u (t) a caror frecventa se variaza. Se citesc la osciloscop
valorile maxime pentru tensiunile de intrare, respectiv de iesire, precum si
defazajul intre cele doua semnale la fiecare frecventa reglata.
Datele se trec in tabelul 5.
Tabel
5.
|
R
|
L
|
C
|
U1max
|
U2max
|
H
|
mas
|
Bmas
|
H )calc
|
calc
|
|
H
|
F
|
V
|
V
|
|
grad
|
Hz
|
|
grad
|
|
|
|
|
|
|
|
|
|
|
Relatii de calcul:
Convertor de ordin I:
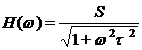
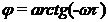
Observatie: Banda de frecventa
B este cuprinsa intre 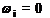 si
si 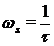 , deoarece:
, deoarece:
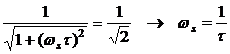
Convertorul de ordin II:
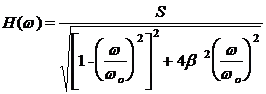
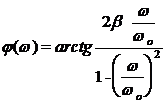 Banda de frecventa B rezulta:
Banda de frecventa B rezulta:
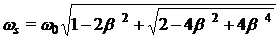
Pentru amortizari slabe,
caracteristica amplitudine - frecventa prezinta un maxim dat de
relatia:
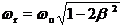
3.Intrebari
recapitulative.
3.1.
Sa se scrie ecuatiile de functionare in domeniul timp pentru
convertoarele de ordinul I si
II.
3.2. Sa se obtina
prin calcul relatiile ce definesc raspunsul la o excitatie
treapta pentru aceste convertoare.
3.3. Deduceti caracteristica de
frecventa pentru convertoarele de ordinul I si II.
3.4.
Care sunt parametrii caracteristici pentru caracterizarea in domeniul timp a convertoarelor de masurare?
3.5.
Care sunt parametrii ce permit caracterizarea in domeniul frecventa a
convertoarelor de masurare?


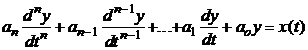
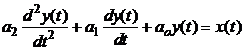


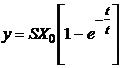


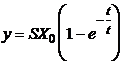
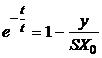
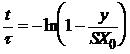

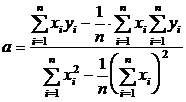
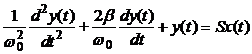
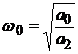
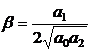 - factor de
amortizare
- factor de
amortizare