Circuite
rezonante RLC
Principalul rezultat al
prelegerii precedente: comportarea in frecventa a circuitelor
descrisa prin functia de raspuns la frecventa.
Exemple: circuitul RC care
atenueza frecventele inalte, incepind cu 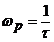 , atenuatorul compensat in frecveta.
, atenuatorul compensat in frecveta.
La cursul de
electrotehnica au fost studiate si alte circuite, cu un singur
element reactiv (un singur element care inmagazineaza energie), pentru
care functia raspuns la frecventa are un numitor de gradul
1 in variabila pulsatie (sau frecventa).
Pentru scopuri de
atenuare selectiva a unor benzi de frecventa se utilizeaza
circuite cu mai mult de un element reactiv. Dintre ele, sint importante cele
numite "rezonante". Ele prezinta fenomenul numit rezonanta, adica
au unul sau mai multe maxime locale in functia raspuns la
frecventa. Frecventa la care apare un astfel de maxim se
numeste frecventa de rezonanta.
Circuitul RLC serie, in regim permanent sinusoidal
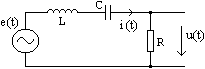
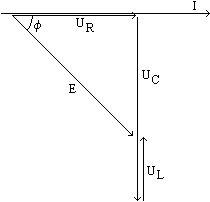
Se observa ca
marimea comuna celor trei elemente este curentul. Diagrama
fazoriala in figura. Ecuatia Kirchhoff II (intre amplitudinile
tensiunilor si curentului):
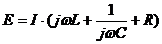 ,
,
de unde 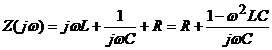 .
.
Se observa ca
exista o frecventa la care efectul inductantei si al
capacitatii se compenseaza reciproc, partea imaginara a
impedantei devine nula, deci impedanta care se vede la borne
este chiar R. Aceasta
frecventa este data de relatia: 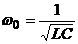 sau
sau 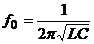 . Valoarea impedantei este minima la rezonanta.
. Valoarea impedantei este minima la rezonanta.
Raspunsul la frecventa
al circuitului, considerind tensiunea pe rezistor ca marime de
iesire:
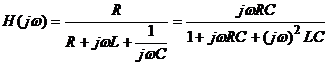 .
.
Se mai poate pune sub
forma:
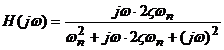 , unde
, unde 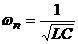 se numeste
pulsatia naturala sau de rezonanta a circuitului iar
se numeste
pulsatia naturala sau de rezonanta a circuitului iar 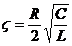 se numeste coeficientul de amortizare.
se numeste coeficientul de amortizare.
Caracteristici de
frecventa: reprezentarea grafica a modulului si defazajului
functiei raspuns la frecventa, in raport cu frecventa.
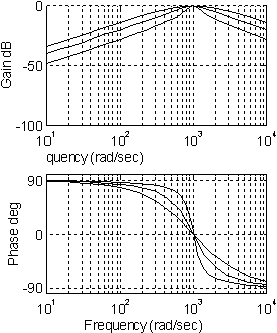
In figura de mai jos, caracteristicile de frecventa, in coordonate
logaritmice, pentru diferite valori ale coeficientului de amortizare: 0,2, 0,5,
1. Pulsatia naturala este de 1000 rad/s. In caracteristica
amplificare-pulsatie, curba cu amplificarea mai mica pentru
coeficient 0,2. In caracteristica faza-pulsatie, curba mai
abrupta pentru coeficient 0,2.
In figura de mai jos, modulul
caracteristicii amplificare-frecventa, in coordonate liniare, intr-o
banda ingusta, in jurul pulsatiei de rezonanta.
Carcteristica de jos pentru coeficient de amortizare 0,2. Se observa caracterul
puternic selectiv. Caracteristica de sus pentru coeficient 1, cind circuitul
este slab selectiv. In mod uzual, in circuitele electronice selective se
folosesc coeficienti de amortizare mult mai mici, deci caracter selectiv
mult mai puternic. Un calcul simplu arata ca:
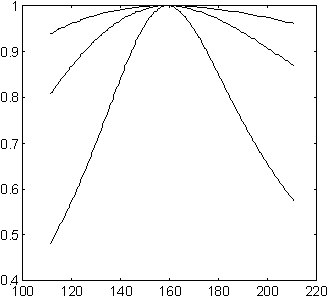
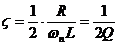 ,
,
adica coeficientul
de amortizare este jumatate din inversul factorului de calitate al
bobinei, calculat la frecventa de rezonanta. Selectivitatea
foarte buna se obtine cu un factor de calitate mare.
Alte
proprietati ale circuitului, aflat in regim permanent sinusoidal, la
frecventa de rezonanta:
defazaj nul intre curent
si tensiunea la borne, defazaj nul intre curent si tensiunea pe
rezistor;
tensiunea pe bobina
egala in modul cu tensiunea pe condensator si defazata cu 180
grade;
energiile medii inmagazinate in
cele doua elemente reactive sint egale;
pe durata unei perioade,
energia inmagazinata se deplaseaza de la bobina la condensator
si invers, schimbul cu exteriorul este nul;
la frecvente mai mici decit
cea de rezonanta, predomina comportarea capacitiva
(curentul si tensiunea de iesire inaintea tensiunii de intrare, maxim
cu 90 grade);
la frecvente mai mari decit cea de
rezonanta, predomina comportarea inductiva (curentul
si tensiunea de iesire in urma tensiunii de intrare, maxim cu 90
grade);
Pentru a ilustra
caracterul selectiv:
Circuitul RLC serie, atacat cu semnal periodic
dreptunghiular
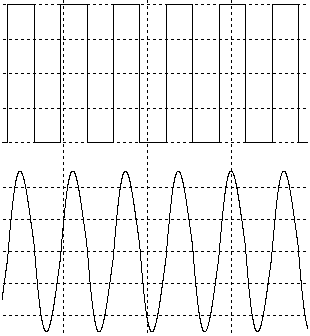
 . Frecventa semnalului de intrare (sus) egala cu
frecventa de rezonanta a circuitului.
. Frecventa semnalului de intrare (sus) egala cu
frecventa de rezonanta a circuitului.
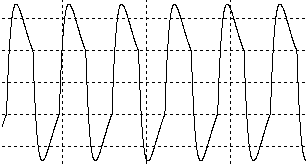
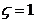 , frecventa de rezonanta
, frecventa de rezonanta
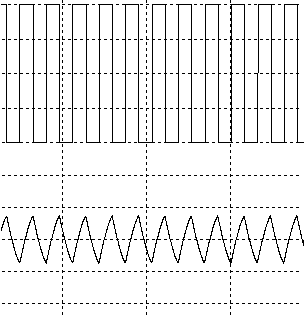
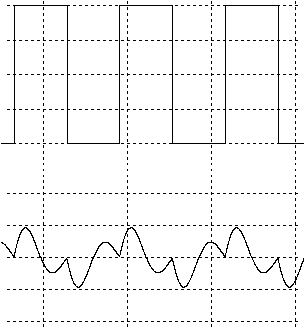
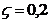 , frecventa de doua ori mai mare decit cea de
rezonanta
, frecventa de doua ori mai mare decit cea de
rezonanta
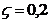 , frecventa de doua ori mai mica decit cea de
rezonanta
, frecventa de doua ori mai mica decit cea de
rezonanta
Utilizari tipice:
cuplare intre doua
circuite, marimea transmisa fiind tensiunea. Semnalul de intrare este
o suma de mai multe componente, dintre care este favorizat semnalul cu
frecventa egala sau apropiata cu cea de rezonanta,
celelalte fiiind atenuate (atenuare foarte mare, daca factorul de calitate
este mare);
selectarea formei pur
sinusoidale a semnalului, dintr-o tensiune periodica nesinusoidala, dar
de frecventa egala cu cea de rezonanta. Semnalul de
iesire este cu atit mai aproape de sinus cu cit coeficientul de amortizare
este mai mic.
Circuitul RLC paralel, in regim permanent sinusoidal
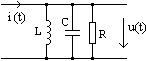
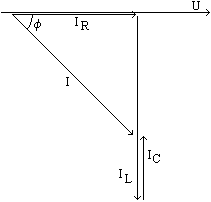
Marimea comuna
celor trei elemente este tensiunea la borne. Impedanta la borne este:
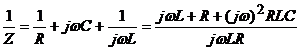 ;
;
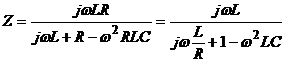 .
.
Din nou, exista o
frecventa la care efectul inductantei si al
capacitatii se compenseaza reciproc, partea imaginara a
impedantei tinde spre infinnit, deci impedanta care se vede la borne
este chiar R. Aceasta
frecventa este data de relatia: 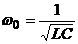 sau
sau 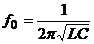 . Valoarea impedantei este maxima la rezonanta.
. Valoarea impedantei este maxima la rezonanta.
Daca
consideram curentul ca marime de intrare iar tensiunea ca marime
de iesire, raspunsul la frecventa este o marime
dimensionala, adica impedanta calculata mai sus. Ea se
poate pune sub forma:
 ,
,
unde pulsatia de
rezonanta este cea de mai sus iar coeficientul de amortizare are
expresia: 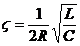 . (Aparent, coeficientul de amortizare ar avea efect invers
fata de cazul precedent, dar trebuie tinut cont de faptul
ca rezistenta R din acest
circuit este in paralel cu bobina, deci poate avea o valoare mare, in timp ce
rezistenta din circuitul serie este de valoare foarte mica. Deci
coeficientul are aceeasi semnificatie cu cea din circuitul
precedent.)
. (Aparent, coeficientul de amortizare ar avea efect invers
fata de cazul precedent, dar trebuie tinut cont de faptul
ca rezistenta R din acest
circuit este in paralel cu bobina, deci poate avea o valoare mare, in timp ce
rezistenta din circuitul serie este de valoare foarte mica. Deci
coeficientul are aceeasi semnificatie cu cea din circuitul
precedent.)
Comportarea circuitului RLC paralel este opusa celei a
circuitului serie. Impedanta are un maxim la frecventa de
rezonanta. Circuitul primeste la intrare un semnal in curent,
suma a mai multor semnale, dintre care selecteaza acel semnal
sinusoidal care are frecventa egala cu frecventa de
rezonanta.
Exercitiu propus
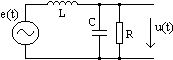
Exprimati impedanta,
functia raspuns la frecventa, caracteristicile de
frecventa, pentru circuitul din figura. Se considera
tensiunea generatorului ca marime de intrare iar tensiunea pe grupul RC ca marime de iesire.
Filtre
In
multe situatii, semnalul de intrare este suma a mai multor
componente, de frecvente diferite. Dintre ele, unele sint utile, altele
dorim sa le rejectam. Circuitele care nu sint exclusiv rezistive (au
componente reactive in compunerea lor) au proprietatea prezentata mai sus,
de a raspunde diferit la semnalele de intrare, in functie de
frecventa lor. Aceasta proprietate este exploatata in filtre. In
general, filtrele sint circuite liniare care atenueaza semnalele dintr-o
banda de frecvente, transmitind neatenuate semnalele din restul
benzii.
Exemple
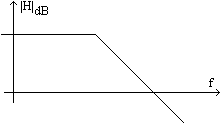
FTJ, care transmite
frecvetele joase si atenueaza frecventele inalte. Circuitul
folosit ca exemplu in paragrafele anterioare este un FTJ. Un exemplu de
utilizare este pastrarea semnalului dat de chitara bas si diminuarea
semnalelor de frecventa mai mare la semnalul muzical.
FTS, care transmite
semnalele de frecvente inalte si le diminueaza pe cele de
frecvente joase. Exemplu de utilizare: circuitul de eliminare a
componentei medii si a semnalelor de frecvente foarte joase (sub 5
Hz) de la intrarea osciloscopului.
FTB, care transmite
semnalele dintr-o banda de frecvente determinata, atenuind pe
cele din afara benzii. Exemple de utilizare: filtru care lasa sa
treaca doar semnalele din banda 20Hz - 20kHz, in amplificatoarele audio,
sau filtrul care lasa sa treaca doar semnalele din banda 450-460
kHz, in amplificatoarele de frecventa intermediara din
receptoarele radio MA.
FOB, care elimina
din semnalul de intrare componentele dintr-o banda fixata. Exemple:
filtre care elimina zgomotul de retea sau zgomotul produs de
aparatele care oscileaza pe o anumita frecventa. Banda de
oprire a filtrului se alege centrata pe frecventa care trebuie
eliminata.
Tehnologie de realizare
pentru filtrele selective (FTB si FOB): ceramica piezoelectrica.
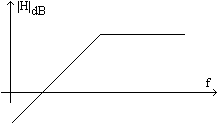
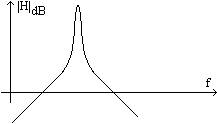
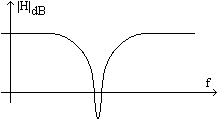
Exemple de functii
raspuns la frecventa, care apartin unor filtre:
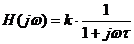 ; (FTJ, ordinul I)
; (FTJ, ordinul I)
 ; (FTS, ordinul I)
; (FTS, ordinul I)
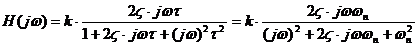 ; (FTB, ordinul II)
; (FTB, ordinul II)
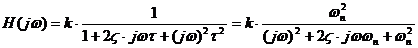 ; (FTJ, ordinul II, posibil cu rezonanta la
pulsatia naturala)
; (FTJ, ordinul II, posibil cu rezonanta la
pulsatia naturala)
Alte
componente electronice
rezonatorul piezoelectric (cuart, ceramice cu efect piezo);
linia de intirziere.
Componente mecanice: carcasa,
radiatoarele, suruburile.
Componente electromecanice:
releul, intrerupatorul, comutatorul (switch), conectorii, borne de test.
Componente electrice:
transformatorul, cablajul, descarcatoare in vid, sigurante fuzibile, becuri,
sunturi, placa de test = breadboard
Cablaj imprimat. Modul
de plantare pe cablaj (pin in gaura, SMD). Componente realizate direct pe
cablaj (inductanta, capacitate - microstrip).
Comportarea
neliniara, solutiile grafice, notiunea de punct de
functionare
Unele componente au
caracteristica neliniara. Sint utilizate special pentru aceasta
proprietate. Exemple: becul cu
incandescenta (baretor), tubul cu descarcare in gaz. Marimile
care caracterizeaza functionarea la un moment dat: punctul de
functionare. Aflarea punctului de functionare: metoda
grafica (chiar si pentru cele care au descriere analitica a
caracteristicii).
Exemplu
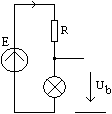
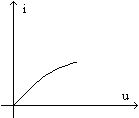
Becul din prelegerea
precedenta, montat intr-un circuit simplu (vezi figura), cu sursa
si un rezistor liniar. Se cer valorile curentului si tensiunilor din
circuit. A fost redesenata caracteristica, in coordonatele i si u.
Formal, cele doua
relatii care descriu functionarea circuitului:
caracteristica neliniara a
becului, 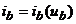
ecuatia Kirchhoff II, 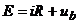 .
.
Prima are expresia
grafica din enunt. A doua are ca expresie grafica o
dreapta, in aceleasi coordonate. Solutia problemei este punctul
de functionare, adica perechea de valori curent - tensiune care
satisface simultan cele doua ecuatii. Grafic, punctul de
functionare este punctul aflat la intersectia celor doua curbe.
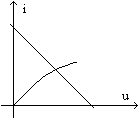
Abilitatea
electronistului de a lucra cu caracteristici neliniare.
Functiuni de circuit
si de prelucrare a semnalelor
Amplificare: mareste puterea
semnalului, de obicei pastrind forma lui (anvelopa).
Oscilatie: produce (genereaza)
semnal de forma dorita, fara a primi alt semnal din exterior
Redresare: furnizeaza semnal de
o singura polaritate, indiferent de polaritatea semnalului de intrare.
Poate avea rol de prelucrare a informatiei sau energetic.
Stabilizare: mentine aceeasi
valoare a unui semnal, indiferent de actiunea perturbatiilor. De
obicei, scop energetic.
Modulare: suprapunere a formei unui
semnal de energie mica (modulator) peste un alt semnal (numit
purtator), astfel incit informatia primului sa se
regaseasca intr-un parametru al semnalului rezultat (numit semnal
modulat). Folosita in radiocomunicatii, aparate de masura,
etc.
Demodulare: recuperarea
informatiei semnalului modulator din semnalul modulat.
Functiuni aritmetice (realizate analogic sau
numeric): adunare, scadere, inmultire, etc.
Conversii AN, NA


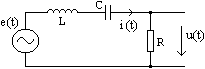

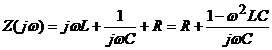 .
.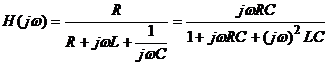 .
.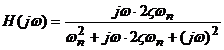 , unde
, unde 





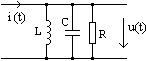

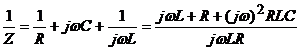 ;
;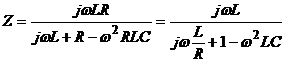 .
. ,
,