Prelucrarea
datelor experimentale - UNITATI DE MASURA
 DEFINITII SI FORMULE
DEFINITII SI FORMULE
Tabelele de date sunt necesare
pentru prezentarea ordonata si sugestiva a rezultatelor
determinarilor experimentale. Exista reguli de intocmire a tabelelor
de date care vor fi prezentate in cuprinsul acestui material.
Reprezentarile
grafice constituie de multe ori un ajutor pretios in efortul de a stabili
corelatii matematice intre datele experimentale. Curba obtinuta
ca grafic poate sugera adesea forma matematica a legii pe care urmam
sa o stabilim in final. De asemenea, reprezentarea grafica a unor
legi ale fizicii sau tehnicii permite gasirea cu usurinta a
unor valori care ar fi identificate relativ dificil in tabele de date (de
exemplu, reprezentarea grafica a presiunii vaporilor saturanti ai
apei in functie de temperatura este o modalitate foarte simpla
de a stabili presiunea de saturatie cunoscand temperatura, in
comparatie cu localizarea aceleiasi valori intr-un tabel de date
intins pe o intreaga pagina de carte). Valoarea unei reprezentari
grafice sta si in modul in care este facuta. Paginile
urmatoare vor cuprinde explicatii care sa va familiarizeze
cu modul corect de realizare a unei reprezentari grafice de calitate.
Utilizand tehnica de calcul si programe adecvate (Excel, Mathcad, Origin, etc.) se pot obtine
reprezentari grafice de foarte buna calitate.
Metoda celor mai
mici patrate sau metoda regresiei liniare
este utilizata pentru trasarea graficelor. O curba experimentala
se traseaza printre punctele experimentale,
lasand de o parte si de alta cam acelasi numar de puncte.
Metoda celor mai mici patrate permite gasirea traseului cel mai
putin departat de fiecare punct in parte, dar care este totusi o
curba continua, fara variatii prea bruste.
Fitarea datelor
experimentale este procedeul prin care dintr-un sir de date experimentale se
pot trage concluzii cu privire la forma matematica a unei anumite legi a
fizicii. In esenta, fitare (din englezescul a potrivi) inseamna
sa cauti functia matematica care sa ofere cea mai
buna corelare intre datele experimentale. Trebuie mentionat ca
functia gasita prin fitare nu
este si in mod necesar adevarata lege dupa care decurge
procesul respectiv ! In functie de domeniul de valori al parametrului
experimental se pot gasi formule aproximative, valabile doar in domeniul
considerat. Diferitele metode de fitare sunt integrate in programe de calcul
cum ar fi Excel, Mathcad, Mathlab si
altele.

ASPECTE TEORETICE
Inregistrarea
datelor experimentale, reprezentare grafica
Inregistrarea
datelor experimentale se face in tabele intocmite in prealabil.
Orice tabel
trebuie sa cuprinda un cap de
tabel. Capul de tabel :
cuprinde in mod obligatoriu simbolul
marimii fizice si unitatea de masura
este asezat in mod obisnuit deasupra
coloanelor rezervate datelor, dar poate fi plasat uneori si la stanga lor
poate cuprinde uneori formula de calcul
utilizata pentru obtinerea valorilor din coloana respectiva
Coloanele
tabelului de date sunt rezervate fie marimilor considerate ca variabile
independente, fie datelor obtinute prin masurare, fie rezultatelor.
Primele coloane din stanga sunt rezervate pentru marimile independente,
iar urmatoarele marimilor masurate. In fine, ultimele coloane cuprind
rezultatele, de multe ori calculate in functie de marimile
masurate. Tabelul de date poate avea un nume, care, de cele mai multe ori,
descrie scopul pentru care sunt facute masuratorile experimentale.
Valorile
marimilor independente sunt trecute in tabel inainte de efectuarea experientei.
Unitatile de masura trebuie astfel alese incat numerele
care sunt trecute in tabel sa nu fie excesiv de mari sau de mici. Astfel,
nu este indicat sa fie trecuta in tabel valoarea (t =) (s), ci valoarea (t =) (ms)
sau valoarea (t =) (10-6 s). Numarul de
zecimale cu care este trecuta in tabel o anumita marime trebuie
sa corespunda preciziei cu care ea a fost determinata. Astfel,
nu este indicat sa fie trecuta in tabel valoarea (v =) (m/s), ci valoarea (v =) (m/s)
daca precizia masuratorii este de ordinul a 1%. In fine, pentru
facilitarea citirii datelor, pe aceeasi coloana, valorile prezentate
vor avea acelasi numar de zecimale, iar virgulele care separa
zecimalele de intregi vor fi plasate una sub alta.
In multe
cazuri prezentarea sau chiar prelucrarea datelor experimentale este facilitata
de reprezentarile grafice.
Avantajele acestora sunt:
permit observarea cu usurinta a
variatiilor marimii studiate in raport cu variatia parametrului
ales, evidentiind eventualele maxime sau minime
curba trasata printre punctele
experimentale este o reprezentare mai exacta a legaturii dintre
marimea studiata si parametru decat fiecare pereche de date
experimentale in parte
sugereaza relatia matematica
dintre marimea studiata si parametru
Intocmirea
unei reprezentari grafice se supune unor reguli practice care vor fi prezentate
in continuare :
T
graficele se traseaza pe hartie
milimetrica sau pe caroiaje intocmite anterior
T
formatul hartiei trebuie sa fie suficient de
mare pentru ca aspectul curbei sa nu aiba de suferit (este recomandat
formatul A5 sau A6)
T
intervalele de valori ale axelor trebuie astfel
alese incat curba obtinuta sa fie repartizata pe intreaga
suprafata a graficului
T
aceasta inseamna si faptul ca
valorile coordonatelor axelor nu trebuie sa inceapa obligatoriu de la
zero, fiind de preferat ca originea axei sa corespunda celei mai mici
valori reprezentate, iar extremitatea sa celei mai mari
T
distanta dintre doua linii ingrosate
pe hartia milimetrica sau distanta dintre doua linii
alaturate ale caroiajului trebuie sa corespunda unui numar
de unitati ale marimii reprezentate care sa permita
reprezentarea cu usurinta a valorilor intermediare (de exemplu,
in cazul hartiei milimetrice, distanta dintre doua linii
ingrosate poate corespunde la o unitate, la doua unitati,
la cinci unitati sau la zece unitati, dar este nepractic ca
ea sa corespunda la sapte unitati)
T
fiecare pereche de date se va reprezenta ca un punct
pe suprafata graficului, iar acest punct va fi bine marcat (insemnat, de
exemplu, cu o steluta)
T
coordonatele punctelor experimentale nu se noteaza pe grafic (ele pot
fi deduse cu ajutorul marcajelor principale de pe axele de coordonate)
T
curba experimentala va fi trasata printre
puncte, lasand de o parte si de alta cam acelasi numar de
puncte
T
este util ca trasarea curbei sa fie
facuta cu un florar
T
se va urmari ca aspectul curbei sa fie cat
mai continuu, fara variatii bruste de panta sau de
curbura
T
daca un punct experimental este plasat mult in
afara curbei, este recomandat ca masuratoarea respectiva sa
fie refacuta
T
daca in acelasi grafic se reprezinta
mai multe curbe, ele vor fi trasate cu culori diferite, iar punctele experimentale
corespunzatoare vor fi marcate in mod diferit
 
|
X
|
12
|
14
|
16
|
18
|
20
|
22
|
24
|
26
|
28
|
|
Y
|
15
|
29
|
21
|
27
|
28
|
36
|
38
|
39
|
50
|
|
|
Cum trebuie facuta
reprezentarea grafica !
|
|

|
Metoda celor
mai mici patrate
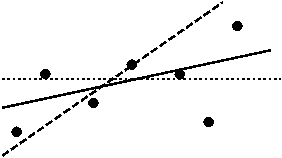
Sa
urmarim exemplul din figura alaturata. Sa presupunem
ca legea fizica pe care o vom pune in evidenta este o lege
liniara. Putem duce printre punctele experimentale mai multe drepte care
sa corespunda criteriilor de intocmire a unei reprezentari grafice.
Care dintre aceste drepte reprezinta
cel mai corect legea cautata
? Metoda celor mai mici patrate raspunde tocmai acestei
intrebari.
Conform metodei celor mai mici patrate, panta
dreptei si coordonata intersectiei sale cu axa Oy vor fi astfel alese incat suma patratelor distantelor
de la fiecare punct experimental la dreapta sa fie minima.
Sa
urmarim figura alaturata. Presupunem ca parametrii xk ai masuratorii
au fost determinati precis (de exemplu, acul instrumentului de
masura era pozitionat exact in dreptul unei gradatii a
scalei). In schimb, marimile corespunzatoare, yk, nu mai sunt stabilite tot atat de precis prin masurare.
Consideram ca valoarea corecta a marimii y corespunde punctului y'k
de pe dreapta. Distanta dintre aceste puncte este :
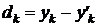
Conform ecuatiei dreptei, obtinem :

si deci :

Suma patratelor distantelor de la dreapta la
toate punctele experimentale este :
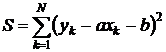
sau :

Impartind la N,
punem in evidenta valorile medii :
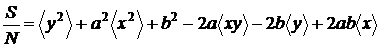
Factorul S/N este o functie de doi parametri
necunoscuti, a si b. Valoarea sa este minima atunci
cand derivatele partiale in raport cu a
si b se anuleaza simultan :
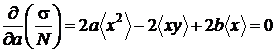

Rezulta :
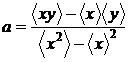
si :
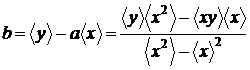
Dreapta
cautata are ecuatia :

unde :

Metoda
celor mai mici patrate se poate utiliza si in cazul altor tipuri de
functii decat cele liniare. De exemplu, in cazul y = cxp,
logaritmam relatia :
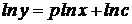
si observam ca ln y este functie liniara de ln x. Constantele p
si ln c pot fi calculate acum
utilizand metoda celor mai mici patrate.
Alte
modalitati de fitare a datelor experimentale
Exista
si numeroase legi ale fizicii care nu sunt exprimabile prin functii
liniare sau exponentiale. Un exemplu ar fi legea spatiului in
miscarea rectilinie uniform variata :

Aceasta lege are o forma
polinomiala. Chiar si legi cu mult mai complicate pot fi puse sub
forma polinomiala, gradul polinomului fiind cu atat mai mare cu cat
intervalul de valabilitate este mai mare si precizia mai necesara. De
exemplu, elongatia unui oscilator armonic 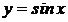 , poate fi aproximata ca functie polinomiala
prin (x masurat in radiani) :
, poate fi aproximata ca functie polinomiala
prin (x masurat in radiani) :

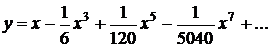
In graficul alaturat, curba ingrosata este
graficul sinusului, iar liniile intrerupte sunt prima si a doua aproximatie
polinomiala. Cea de-a treia aproximatie se suprapune exact peste
graficul sinusului. Se poate face si o teorie care sa explice modul
prin care se gasesc coeficientii polinomului in functie de
datele experimentale. Rezultatele acestei teorii sunt implementate in programe
de calcul tabelar, cum ar fi programul Excel.
EXEMPLU
Sa
presupunem ca dorim sa verificam experimental legea perioadei
micilor oscilatii ale unui pendul gravitational :
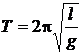
Valoarea acceleratiei
gravitationale este cunoscuta : g
= 9,8 m/s. In cursul experientei vom varia (si masura) lungimea
firului de suspensie si vom calcula perioada impartind timpul
necesar efectuarii unui anumit numar de oscilatii complete la
acest numar. Trebuie sa demonstram prin experiment ca
perioada T este o functie
lineara de 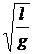 si sa
gasim ca panta dreptei respective este egala cu 2p. In
acest scop, vom folosi metoda regresiei lineare. Ceasul cu care lucram are
precizia de 1 secunda, iar lungimea firului se poate masura cu
precizie de 1 centimetru. Pentru fiecare lungime a firului de suspensie vom
face cate 5 masurari ale perioadei. Sa presupunem ca am obtinut
urmatoarele date experimentale :
si sa
gasim ca panta dreptei respective este egala cu 2p. In
acest scop, vom folosi metoda regresiei lineare. Ceasul cu care lucram are
precizia de 1 secunda, iar lungimea firului se poate masura cu
precizie de 1 centimetru. Pentru fiecare lungime a firului de suspensie vom
face cate 5 masurari ale perioadei. Sa presupunem ca am obtinut
urmatoarele date experimentale :
T
Pentru lungimea de 109 cm, 5 oscilatii se fac
in 10 s, 6 oscilatii in 12 s, 7 oscilatii in 15 s, 8 oscilatii
in 16 s si 9 oscilatii in 19 s
T
Pentru lungimea de 132 cm, 5 oscilatii se fac
in 11 s, 6 oscilatii in 14 s, 7 oscilatii in 16 s, 8 oscilatii
in 18 s si 9 oscilatii in 20 s
T
Pentru lungimea de 182 cm, 5 oscilatii se fac
in 13 s, 6 oscilatii in 16 s, 7 oscilatii in 19 s, 8 oscilatii
in 21 s si 9 oscilatii in 24 s
T
Pentru lungimea de 236 cm, 5 oscilatii se fac
in 15 s, 6 oscilatii in 18 s, 7 oscilatii in 21 s, 8 oscilatii
in 24 s si 9 oscilatii in 27 s
T
Pentru lungimea de 295 cm, 5 oscilatii se fac
in 17 s, 6 oscilatii in 21 s, 7 oscilatii in 24 s, 8 oscilatii
in 27 s si 9 oscilatii in 31 s
Prima
problema pe care o intalnim este aceea de a pune aceste date intr-o
forma mai ordonata, de a calcula perioadele corespunzatoare
si eroarea masurarii. Va pot recomanda sa lucrati
in modul urmator :
T
Deschideti programul Excel
T
Inscrieti in casutele de la A4 la A8
numerele curente ale determinarilor : 1,2,3,4,5
T
Inscrieti in casutele B2, E2, H2, K2,
N2, lungimile firului : 1,09 (m), 1,32 (m), 1,82 (m), 2,36 (m) si 2,95 (m)
T
Inscrieti in casutele B4-8, E4-8,
H4-8, K4-8, N4-8 numerele de oscilatii
T
Inscrieti in casutele C4-8, F4-8,
I4-8, L4-8, M4-8 intervalele de timp corespunzatoare
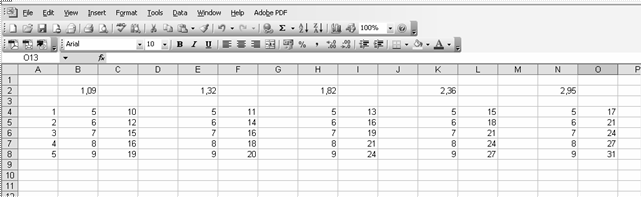
T
Foaia Excel arata acum asa :
T
Selectati casuta D4, si apoi
dati un click in caseta fx,
dupa care tastati semnul "="
T
Selectati casuta C4,
apasati tasta de impartire si apoi selectati
casuta B4. Tastati "Enter"
T
Selectati din nou casuta D4
T
Foaia Excel arata acum asa :
T
Remarcati patratelul din
coltul dreapta-jos al casutei D4. Duceti pointer-ul
mouse-ului pe acest patratel (observati ca el se
transforma intr-o cruciulita), apasati butonul stang
al mouse-ului si, tinandu-l apasat, trageti coltul
(patratelul) in jos, pana la casuta D8.
Eliberati butonul mouse-ului, si selectati o
casuta libera
T
Foaia Excel arata acum asa :
T
Coloana D cuprinde acum valorile perioadelor pentru
cele cinci determinari corespunzatoare lungimii de 1,09 m
T
Eroarea de masurare este destul de mare (1
secunda la 10 pana la 19 secunde). De aceea numarul mare de
zecimale este inutil. Considerand ca eroarea este de ordinul a 1%,
inseamna ca numai primele trei cifre ale unui numar sunt
semnificative. De aceea, valoarea 2,142857 trebuie rotunjita la 2,14.
Pentru a realiza aceasta procedati astfel :
T
Mai intai selectati toate casutele de
la D4 la D8
T
Apoi, deschideti meniul "Format" si
alegeti optiunea "Cells . "
T
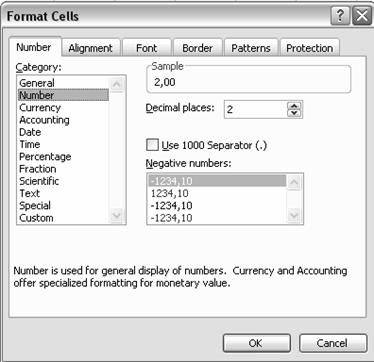
Se va deschide o fereastra noua : "Format
Cells"
T
In meniul "Category" alegeti optiunea
"Number", iar in caseta "Decimal places" introduceti valoarea 2
T
Apasati butonul "OK"
T
Rezultatul va fi ca toate numerele in coloana D
sunt acum rotunjite pana la doua zecimale
T
Realizati aceleasi operatiuni pe
coloanele G, J, M si P (evident folosind coloanele de date
corespunzatoare).
T
Pe pagina urmatoarea puteti vedea modul in
care arata foaia Excel in acest
moment.
T
Este momentul sa alcatuim un tabel care
sa contina si alte elemente decat acelea cuprinse de
programul Excel
T
Fara a inchide programul Excel, deschideti programul Word, iar pentru mai multa siguranta
tastati de cateva ori "Enter"
T
Reveniti la Excel
si selectati toate casutele intre A1 si P8
T
Dati comanda "Copy" (aflata si pe
bara "Standard", sau in meniul "Edit"
T
Reveniti in Word si dati comanda
"Lipire" (sau "Paste"). Rezultatul va fi urmatorul :
T
Nu arata prea bine, dar nu va
descurajati !
T
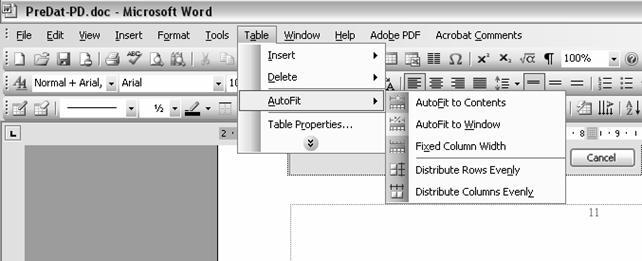
Selectati prima casuta a
tabelului, deschideti meniul "Table" :
T
Alegeti optiunea "AutoFit" si, apoi,
"AutoFit to Window"
T
Rezultatul operatiunii este prezentat in
continuare :
T
Selectati toate celulele tabelului
T
Din bara "Table and Borders" alegeti
optiunile si +, apoi din
bara "Formatting" alegeti optiunile "Center" si "Times New
Roman" "10". Tabelul capata infatisarea :
T
Pe linia a treia a tabelului, incepand cu coloana a
doua, inscrieti urmatoarele informatii (caracterele
grecesti se pot selecta prin apasarea butonului W din bara "Standard") :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T
Selectati prima linie a tabelului si
dati comanda "Merge Cells" (evidentiata in bara "Table and
Borders"). Veti obtine :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T
Selectati prima linie din tabel si
inscrieti textul "PERIOADELE DE
OSCILATIE, IN FUNCTIE DE LUNGIMEA FIRULUI DE SUSPENSIE" (textul este scris
in "Times New Roman", marimea "10")
|
PERIOADELE DE OSCILATIE, IN FUNCTIE DE LUNGIMEA FIRULUI DE
SUSPENSIE
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T
In linia a doua, contopiti casutele
2-5, 6-8, 9-11, 12-14 si 15-17 prin selectare si aplicarea comenzii
"Merge Cells" :
|
PERIOADELE DE OSCILATIE, IN FUNCTIE DE LUNGIMEA FIRULUI DE
SUSPENSIE
|
|
|
|
|
|
|
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T
Adaugati unitatea de masura a
lungimii :
|
PERIOADELE DE OSCILATIE, IN FUNCTIE DE LUNGIMEA FIRULUI DE
SUSPENSIE
|
|
1,09 (m)
|
1,32 (m)
|
1,82 (m)
|
2,36 (m)
|
2,95 (m)
|
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T
In casuta a doua din prima coloana,
inscrieti textul "l
T
In casuta a treia din prima coloana
inscrieti textul " N.C. ".
Obtineti :
|
PERIOADELE DE OSCILATIE, IN FUNCTIE DE LUNGIMEA FIRULUI DE
SUSPENSIE
|
|
l
|
1,09 (m)
|
1,32 (m)
|
1,82 (m)
|
2,36 (m)
|
2,95 (m)
|
|
N.C.
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T
Cu aceasta, primul tabel de date al lucrarii
este terminat. Daca doriti ca el sa fie mai sugestiv il
puteti pune sub forma (cum veti reusi este deja un
exercitiu pentru dumneavoastra !) :
|
PERIOADELE DE OSCILATIE, IN FUNCTIE DE LUNGIMEA FIRULUI DE
SUSPENSIE
|
|
l
|
1,09 (m)
|
1,32 (m)
|
1,82 (m)
|
2,36 (m)
|
2,95 (m)
|
|
N.C.
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
N
|
Dt (s)
|
T
(s)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T
Este deja momentul sa ne indreptam
catre finalizarea prelucrarii datelor
T
Va trebui sa determinam valorile medii ale
perioadelor, eroarea de masura si valorile factorului 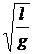
T
Pentru inceput deschideti din nou tabelul Excel
T
In coloana A12-16 inscrieti numerele curente
1,2,3,4,5
T
In coloana D12-16 inscrieti valorile lungimilor
firului de suspensie
T
Selectati casuta E12 si apoi
dati un click in caseta fx,
tastati "=", apoi scrieti SQRT(D12/9,81) si finalizati
tastand "Enter"
T
Selectati din nou casuta E12 si
trageti coltul din dreapta-jos, acoperind coloana E, pana la E16
T
Rotunjiti la doua zecimale numerele din
coloana E. In acest moment aveti calculate valorile lui 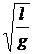 pentru toate cele
cinci lungimi considerate
pentru toate cele
cinci lungimi considerate
T
Pentru a calcula valorile medii ale perioadelor,
precum si abaterile patratice medii, procedati asa cum v-a
fost indicat in lucrarea "Teoria erorilor de masura". Mediile
perioadelor le treceti in coloana B, iar abaterile patratice in
coloana C. Daca este nevoie, rotunjiti din nou rezultatele la
doua zecimale
T
Portiunea din foaia Excel cu care ati
lucrat ar trebui sa arate asa :
T
Este momentul sa importati acest tabel in
documentul Word
T
Selectati toate casutele de la A10 la
E16 si procedati in acelasi mod ca la operatia anterioara
de importare si formatare a unui tabel de date
T
Ar trebui sa obtineti :
|
PERIOADELE DE OSCILATIE SI ABATEREA PATRATICA
MEDIE
|
|
Nr. crt.
|
<T> (s)
|
sT
|
l
(m)
|
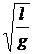 (s) (s)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T
Ultima etapa consta in trasarea
graficului, utilizand metoda celor mai mici patrate
T
Reveniti la foaia Excel
T
Deschideti meniul "Insert" si alegeti
optiunea "Chart"
T
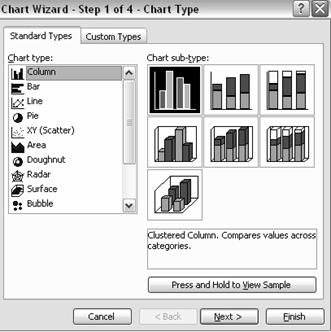
Se va deschide o noua fereastra :
T
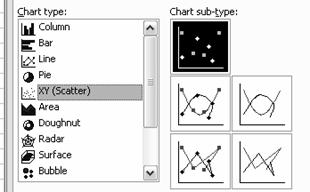
In lista "Chart type" alegeti optiunea "XY
(Scatter)". Pe ecranul monitorului apare :
T
Daca casuta aflata sub
inscriptia "Chart sub-type" este innegrita apasati butonul
"Next >". In caz contrar,
selectati mai intai casuta si apoi apasati "Next >
T
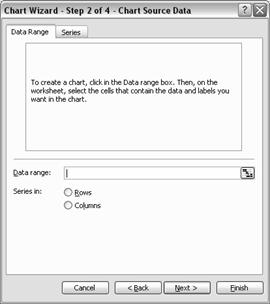
Infatisarea ferestrei cu care
lucrati se modifica dupa cum urmeaza :
T
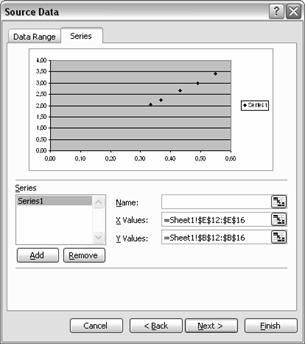
Dati un click pe "Series"
T
Fereastra isi schimba infatisarea
si arata ca in imaginea din dreapta. Apasati butonul "Add"
si din nou veti observa ca fereastra isi schimba
infatisarea :
T
Trebuie acum sa introduceti datele
experimentale Acestea se introduc in casetele "X Values" si "Y Values".
Procedati astfel :
T
Dati un click in caseta "X Values"
T
Apoi selectati toate valorile numerice din
coloana E12-16 (adica valorile factorului 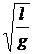 )
)
T
Dupa aceea dati un click in caseta "Y
Values" si selectati tot cuprinsul ei
T
In continuare, selectati toate valorile
numerice din coloana B12-16
T
Dupa aceste operatii, fereastra din foaia
Excel ar trebui sa arate ca in imaginea urmatoare :
T
Apasati butonul "Next"
T
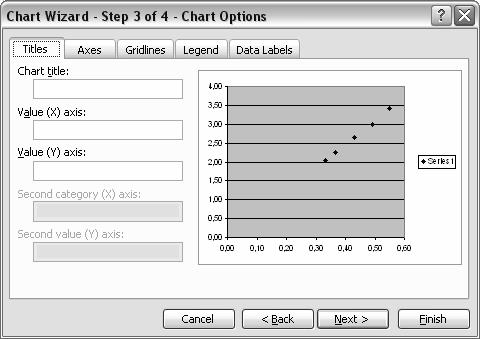
Fereastra isi schimba din nou infatisarea
T
In meniul "Titles", caseta "Chart title",
scrieti "PERIOADA DE OSCILATIE A PENDULULUI GRAVITATIONAL IN
FUNCTIE DE LUNGIMEA FIRULUI DE SUSPENSIE"
T
Treceti la meniul "Gridlines" si
marcati casuta "Major gridlines" de sub titlul "Value (X) axis"
T
In meniul "Legend", deselectati optiunea
"Show legend"
T
In fine, apasati butonul "Finish"
T
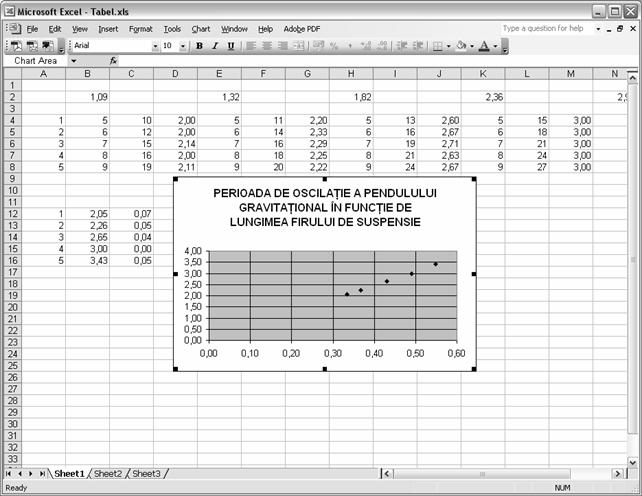
Fereastra "Chart Options se inchide si pe foaia
Excel apare un grafic
T
Pe pagina urmatoare puteti vedea
infatisarea pe care o capata acum foaia Excel
T
Graficul mai trebuie prelucrat pentru a ajunge la
forma finala
T
Mai intai, fixand cursorul mouse-ului pe el il
veti "trage" intr-o portiune a foii, in care sa nu obtureze
tabelele de date
T
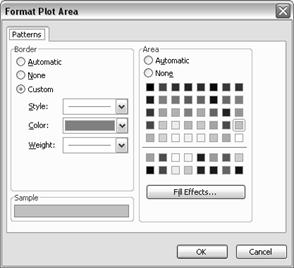
Apoi, veti da un dublu click pe suprafata
sa in portiunea cenusie, fara ca varful cursorului sa
atinga nici liniile de marcaj, nici punctele experimentale :
T
Se va deschide o noua fereastra :
T
Selectati optiunea "None" din zona "Area"
si apoi apasati butonul "OK"
T
Dati un dublu click pe una din liniile de
marcaj verticale
T
Din nou se deschide o fereastra, in care
alegeti tab-ul "Scale" :
T
Aceasta fereastra va solicita
sa alegeti valorile extreme pe axa Ox. Deoarece x = 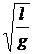 are valoarea
minima egala cu 0,33 si cea maxima egala 0,55, este
bine sa inscrieti in caseta "Minimum" valoarea 0,3, iar in caseta
"Maximum" valoarea 0,6
are valoarea
minima egala cu 0,33 si cea maxima egala 0,55, este
bine sa inscrieti in caseta "Minimum" valoarea 0,3, iar in caseta
"Maximum" valoarea 0,6
T
Apasati butonul "OK"
T
Dati acum un dublu click pe o linie de marcaj
orizontala
T
Va aparea o fereastra
asemanatoare cu cea anterioara, dar care face referire la
valorile minima sau maxima ale lui y = T. Dati valoarea
minima 2 si cea maxima 3,6, dupa care apasati din
nou butonul "OK"
T
Zona graficului se modifica asa cum este
aratat mai jos :
T
Urmeaza sa trasati dreapta prin metoda
celor mai mici patrate si sa aflati panta ei
T
Pentru inceput dati un click-dreapta pe unul
dintre punctele experimentale
T
Apare pe ecran o caseta avand si optiunea
"Add Trendline". Selectati-o !
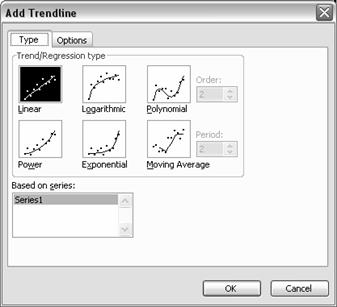
T
Din nou se deschide o fereastra, numita
Add Trendline" :
T
Marcati casuta "Linear" si apasati
butonul "OK"
T
Rezultatul este aparitia pe grafic a unei
drepte, care este chiar dreapta cautata :
T
Pentru a afla panta acestei drepte procedati
astfel :
T
Dati un click intr-un punct oarecare al dreptei
T
Se deschide o caseta, in care selectati
optiunea "Format Trendline"
T
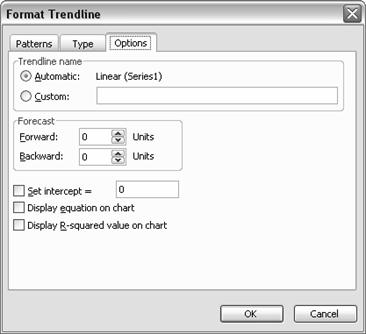
Efectul este deschiderea unei noi ferestre,
numita "Format Trendline"
T
Selectati tab-ul "Options", iar fereastra va
arata ca in figura alaturata
T
Selectati casuta "Display equation on
chart", dupa care apasati butonul "OK"
T
Fereastra se inchide, iar in interiorul graficului
apare o casuta de text, care, de obicei nu este pozitionata
convenabil
T
De aceea, asezati cursorul mouse-ului pe
ea, apasati butonul stang si, tinandu-l apasat
"trageti" casuta de text intr-o pozitie convenabila.
Puteti chiar formata textul din casuta, schimband fontul
si marimea acestuia, inlocuind literele care de la bun inceput sunt
"y" si "x" prin acelea pe care le doriti dumneavoastra. De
asemenea se poate reduce numarul zecimalelor. Dupa aceste
operatii, graficul ar trebui sa arate asa :
T
Ultima etapa pe care trebuie s-o
parcurgeti este importul graficului in documentul Word
T
Pentru aceasta, dati un click in interiorul
suprafetei graficului
T
Veti observa ca el arata ca in figura
de mai sus
T
Dati comanda "Copy"
T
Redeschideti documentul Word si dati
comanda "Lipire" ("Paste")
T
Rezultatul va fi urmatorul :

T
Dati un click pe suprafata figurii (in
acest mod o selectati) si apoi incadrati-o intr-un chenar
(comanda "Insert Frame") :
T
In acest moment, graficul poate fi deplasat in orice
punct al foii si poate fi redimensionat.
T
Redimensionarea se face prin selectarea graficului
si actiunea asupra celor opt patratele care sunt
marcate pe marginile cadrului
T
O alta modalitate de redimensionare este
selectarea graficului, urmata de deschiderea meniului "Format" si
alegerea comenzii "Picture". Se va deschide o fereastra care va
ofera informatii despre modul in care puteti face
redimensionarea, precum si alte operatii.
In mare, cam acestea sunt
operatiunile necesare pentru a face o prezentare de calitate a
rezultatelor pe care le-ati obtinut in urma masuratorilor
experimentale. Mai ramane de discutat un aspect : valoarea pe care am
obtinut-o pentru panta este de 6,323, putin diferita
fata de cea teoretica : 2p = 6,283. Evident,
diferenta se datoreaza erorilor experimentale. Eroarea relativa
este :

Avand in vedere
ca abaterea patratica medie la determinarea perioadei a avut
chiar si valori de 7%, rezultatul obtinut este neobisnuit de bun
pentru conditiile experimentale mentionate la inceputul acestui
material.
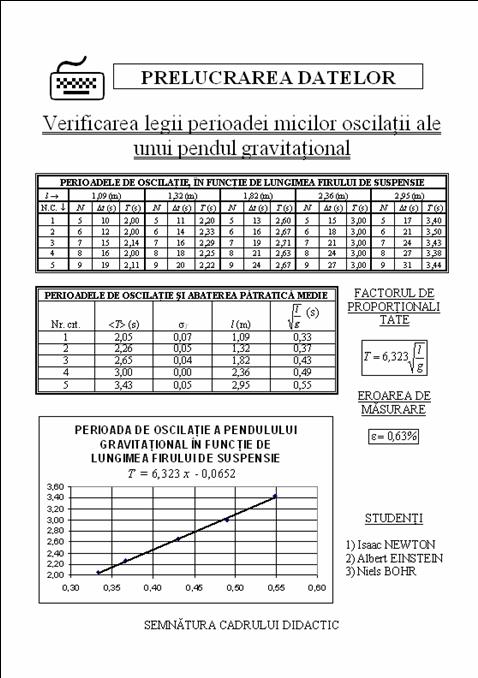
In fine, cum trebuie sa arate in
cele din urma modul de prezentare a rezultatelor?
Iata un exemplu
:

TEME
Urmariti
pas cu pas instructiunile expuse in exemplul precedent si incercati
sa obtineti o pagina de prezentare a datelor,
asemanatoare cu cea pe care v-o sugereaza acest referat. Nu ar
fi neindicat sa va stabiliti o cale proprie, chiar diferita
de aceea pe care am expus-o. Nu uitati ca Isaac Newton, Albert
Einstein si Niels Bohr nu aveau la dispozitie decat creionul si
hartia !
Legea Boyle-Mariotte (valabila
pentru transformarea izoterma a unei cantitati de gaz ideal) are
forma pV = const. Incercati
sa verificati experimental aceasta lege. Variati volumul
ocupat de gaz cu cate 1 cm3, incepand de la 29 cm3
pana la 20 cm3. La volumul de 29 cm3, presiunea
gazului este egala cu presiunea atmosferica normala : 760 mmHg
(760 torr). Masurarea diferentei de presiune intre gazul examinat
si presiunea atmosferica consta in determinarea diferentei
de nivel intre mercurul cuprins in doua ramuri ale unui tub in forma
de U. Diferentele de nivel inregistrate experimental sunt : 0, 27 mm, 56
mm, 88 mm, 122 mm, 138 mm, 199 mm, 242 mm, 290 mm, 342 mm. Intocmiti un
tabel de date si verificati in ce masura produsul dintre
presiune si volum este constant. Calculati abaterea
patratica medie. Reprezentati grafic functia p = p(V). Considerand ca p este o functie de o putere
necunoscuta a lui V,
determinati aceasta putere. Puteti folosi in acest scop metoda
celor mai mici patrate.
Vom
prezenta in continuare un tabel cu date experimentale privind presiunea
vaporilor saturanti ai apei la diverse temperaturi. Tabelul mai cuprinde
si umiditatea absoluta a aerului, exprimata in g(apa)/cm3.
Se cere sa prelucrati datele oferite in acest tabel. Trebuie sa
obtineti graficul presiunii vaporilor saturanti in functie
de temperatura si graficul umiditatii absolute in
functie de temperatura. De asemenea, trebuie sa determinati
functiile polinomiale de gradele 1 pana la 5 care ofera legile
de variatie ale presiunii vaporilor saturanti si
umiditatii absolute in functie de temperatura. Apreciati
ce grad are polinomul care exprima cel mai simplu aceste legi.
Presiunea si umiditatea
absoluta a vaporilor de apa saturanti la diferite temperaturi
|
Temperatura
(°C)
|
Presiunea
(torr)
|
Umiditatea absoluta
(g/m3)
|
Temperatura
(°C)
|
Presiunea
(torr)
|
Umiditatea absoluta
(g/m3)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dupa
ce ati rezolvat problema precedenta, verificati care
aproximatie polinomiala va ofera, si cu ce precizie,
presiunea vaporilor saturanti ai apei la temperatura de 100 C : 760 torr. Daca
rezultatul nu va satisface, ce explicatie puteti da ?
Stiind
ca apa fierbe la temperatura la care presiunea vaporilor saturanti
egaleaza presiunea atmosferica si ca presiunea
atmosferica variaza dupa legea 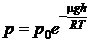 , unde p0
= 760 torr, m = 29 kg/kmol, g = 9,8 m/s2, R = 8310 J/kmol K si T = 300 K, iar h este altitudinea fata de nivelul marii,
aflati la ce altitudine, fierband un ou, indiferent de intervalul de timp,
acesta va ramane crud ? Temperatura minima la care trebuie sa
fiarba un ou pentru a se intari este de minimum 70 C.
, unde p0
= 760 torr, m = 29 kg/kmol, g = 9,8 m/s2, R = 8310 J/kmol K si T = 300 K, iar h este altitudinea fata de nivelul marii,
aflati la ce altitudine, fierband un ou, indiferent de intervalul de timp,
acesta va ramane crud ? Temperatura minima la care trebuie sa
fiarba un ou pentru a se intari este de minimum 70 C.
Umiditatea relativa este raportul
procentual intre presiunea partiala a vaporilor de apa la o
anumita temperatura si presiunea vaporilor saturanti la
aceeasi temperatura. Presiunea partiala se calculeaza
dupa ecuatia de stare a gazului perfect 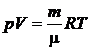 , unde m este masa
gazului (sau vaporilor), iar V este
volumul ocupat de tot amestecul de gaze (vapori). Masa molara a aerului
este 29 kg/kmol, iar masa molara a apei este 18 kg/kmol. Presupunand
ca la temperatura de 20 C umiditatea absoluta este de 20% si ca
amestecul aer-apa este separat de exterior, determinati umiditatea
absoluta a amestecului la 40 C. Confortul termic depinde de umiditatea relativa
(cu cat umiditatea relativa este mai mare, cu atat avem o senzatie de
zapuseala mai accentuata). La care dintre cele doua
temperaturi confortul termic este mai favorabil ?
, unde m este masa
gazului (sau vaporilor), iar V este
volumul ocupat de tot amestecul de gaze (vapori). Masa molara a aerului
este 29 kg/kmol, iar masa molara a apei este 18 kg/kmol. Presupunand
ca la temperatura de 20 C umiditatea absoluta este de 20% si ca
amestecul aer-apa este separat de exterior, determinati umiditatea
absoluta a amestecului la 40 C. Confortul termic depinde de umiditatea relativa
(cu cat umiditatea relativa este mai mare, cu atat avem o senzatie de
zapuseala mai accentuata). La care dintre cele doua
temperaturi confortul termic este mai favorabil ?






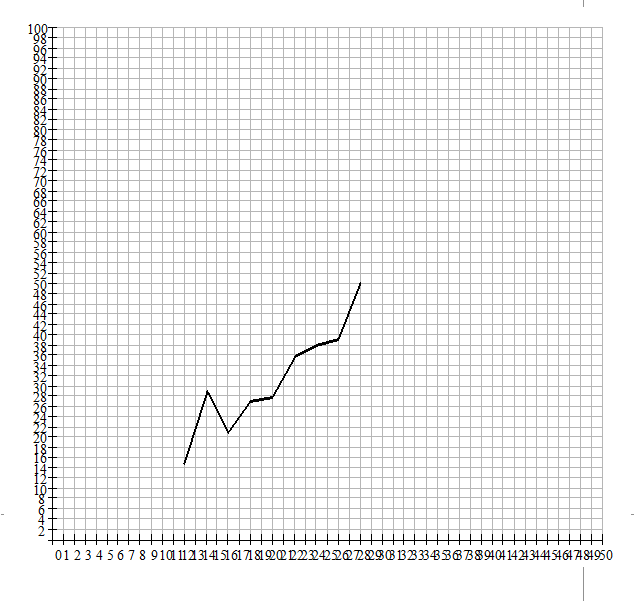




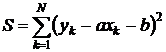

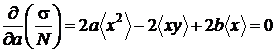

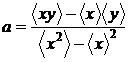
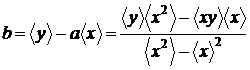




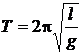















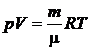 , unde m este masa
gazului (sau vaporilor), iar V este
volumul ocupat de tot amestecul de gaze (vapori). Masa molara a aerului
este 29 kg/kmol, iar masa molara a apei este 18 kg/kmol. Presupunand
ca la temperatura de 20
, unde m este masa
gazului (sau vaporilor), iar V este
volumul ocupat de tot amestecul de gaze (vapori). Masa molara a aerului
este 29 kg/kmol, iar masa molara a apei este 18 kg/kmol. Presupunand
ca la temperatura de 20