TESTAREA IPOTEZEI PRIVIND
DIFERENTA DINTRE DOUA MEDII PENTRU ESANTIOANE DE VOLUM REDUS
In cazul in care dorim sa testam
semnificatia diferentei dintre mediile a doua esantioane de
volum redus, va trebui sa construim, ca si in cazul anterior, o
statistica t, Student. Pentru aceasta vom presupune ca:
- ambele colectivitati generale din care
s-au extras esantioanele sunt normal sau aproximativ normal distribuite;
- dispersiile in cele doua
colectivitati generale sunt egale;
- esantioanele aleatoare sunt selectate
independent unul de celalalt.
In conditiile in care presupunem ca cele
doua colectivitati generale au dispersii egale (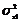 =
= 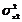 =
= ), un estimator al dispersiei (variabilitatii)
totale din cele doua populatii combinate este:
), un estimator al dispersiei (variabilitatii)
totale din cele doua populatii combinate este:

sau
 .
.
Asadar, dispersia combinata  este media
aritmetica pon-derata a dispersiilor celor doua
esantioane,
este media
aritmetica pon-derata a dispersiilor celor doua
esantioane, 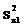 si
si  .
.
Daca dispersiile nu sunt egale (σ2x1≠σ2x2),
atunci testul statistic are forma:
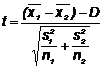
cu gradele de libertate:
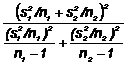
Ipotezele statistice vor fi, in aceste conditii:
- pentru test bilateral;
H0: μ1 = μ2
(μ1 μ2
= D),
H1: μ1 ≠ μ2
(μ1 μ2
≠ D),
- pentru test unilateral dreapta;
H0: μ1 = μ2
(μ1 μ2
= D),
H1: μ1 > μ2
(μ1 μ2
> D),
- pentru test unilateral stanga;
H0: μ1 = μ2
(μ1 μ2
= D),
H1: μ1 < μ2
(μ1 μ2
< D).
Testul statistic t va avea forma:
 .
.
Regiunea critica este data de:
- pentru test bilateral:
t< -t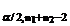 sau t> t
sau t> t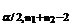 ;
;
- pentru test bilateral dreapta: t> t ;
;
- pentru test bilateral stanga: t< - t .
.
Exemplu:
Presupunem ca dorim sa
testam ipoteza conform careia intre doua marci de
autoturisme nu exista diferente semni-ficative privind cheltuielile
de functionare. Pentru aceasta 20 de posesori de autoturisme (8 posesori
ai primei marci si 12 posesori ai celei de-a doua) sunt rugati
sa tina, cu acuratete, evidenta cheltuielilor de
functionare pe o perioada de un an de zile. Pentru α=0,1
(probabilitate de garantare a rezultatelor (1-α)100 = 90%) sa se
testeze aceasta ipoteza, daca rezultatele prelucrarii
datelor in esantioane sunt:
Marca 1 Marca 2
n1=8 n2=12
 mil. lei
mil. lei 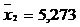 mil. lei
mil. lei
sx1=0,485
mil. lei sx2=0,635 mil. lei

Ipotezele
statistice sunt:
H0: μ1
= μ2 (μ1 - μ2 = 0),
H1: μ1
≠ μ2 (μ1 - μ2 ≠ 0)
[μ1> μ2
sau μ1< μ2].
Testul statistic este:

Cum tα/2,n1+n2-2=
t0,05;18 = 1,734, se observa ca t < tα/2,n1+n2-2, asadar nu
ne aflam in regiunea critica.
Rezulta, deci, ca nu
exista suficiente dovezi pentru a concluziona ca sunt diferente
semnificative intre cheltuielile de functionare ale celor doua
marci de autoturisme.
Trebuie sa facem o remarca asupra
presupunerilor privind normalitatea distributiei in colectivitatea
generala: teoria statistica a dezvoltat teste pentru verificarea normalitatii
distributiilor, teste prin care se verifica ipoteza nula
conform careia legea de
repartitie este cea normala N(μ, σ2), cu μ si 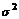 parametrii
necunoscuti ce urmeaza a fi estimati pe baza datelor
esantionului considerat. Cele mai cunoscute teste pentru verificarea normalitatii
sunt: testul χ2 de concordanta cu legea normala,
testul Kolmogorov Smirnov, testul de
normalitate al lui Lilliefors.
parametrii
necunoscuti ce urmeaza a fi estimati pe baza datelor
esantionului considerat. Cele mai cunoscute teste pentru verificarea normalitatii
sunt: testul χ2 de concordanta cu legea normala,
testul Kolmogorov Smirnov, testul de
normalitate al lui Lilliefors.
Daca ipoteza
nula nu este acceptata, vom putea apela la teste statistice neparametrice, in cadrul carora nu se fac
presupuneri speciale asupra formei distributiei.
TESTAREA IPOTEZEI PRIVIND
DISPERSIA UNEI POPULATII
Suma patratelor diferentelor  (care este, de fapt,
egala cu
(care este, de fapt,
egala cu 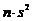 sau
sau  pentru esantioane
mici), impartita la dispersia colectivitatii generale,
are o distributie hi-patrat (
pentru esantioane
mici), impartita la dispersia colectivitatii generale,
are o distributie hi-patrat ( ) (daca populatia esantionata este normal
distribuita).
) (daca populatia esantionata este normal
distribuita).
Asadar, testul statistic utilizat in testarea
ipotezei privind  este:
este:
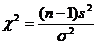 ,
,
care are o distributie  cu (n-1) grade de
libertate, cand populatia esantionata este normal
distribuita, cu dispersia
cu (n-1) grade de
libertate, cand populatia esantionata este normal
distribuita, cu dispersia 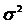 .
.
Valoarea lui  pentru care aria de
sub curba (situata la dreapta ei) este egala cu α, se
noteaza
pentru care aria de
sub curba (situata la dreapta ei) este egala cu α, se
noteaza  . Nu putem folosi notatia
. Nu putem folosi notatia  pentru a reprezenta
punctul la care aria din stanga este α, deoarece statistica
pentru a reprezenta
punctul la care aria din stanga este α, deoarece statistica  este intotdeauna mai
mare decat zero. Dar
este intotdeauna mai
mare decat zero. Dar 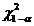 reprezinta
punctul pentru care aria de sub curba situata la stanga lui este
α.
reprezinta
punctul pentru care aria de sub curba situata la stanga lui este
α.
Spre exemplu:
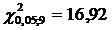
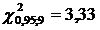
Ipoteza nula este:
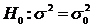
cu ipoteze alternative:
pentru test bilateral 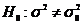 ,
,
pentru test unilateral drept 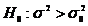 ,
,
pentru test unilateral stang  .
.
Regiunea critica este data de:
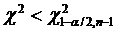 sau
sau 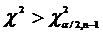 pentru test bilateral,
pentru test bilateral,
 pentru test unilateral
dreapta,
pentru test unilateral
dreapta,
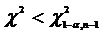 pentru test unilateral
stanga.
pentru test unilateral
stanga.
Exemplu:
Pentru urmatoarele date
privind cererea unui produs (selectate dintr-o colectivitate normal
distribuita), sa se testeze (pentru o probabilitate de 95%),
ipotezele:
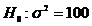 ,
,
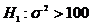 .
.
Datele sunt: 85, 59, 66, 81, 35,
57, 55, 63, 63, 66.
In esantion: 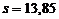 ,
, 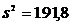 .
.
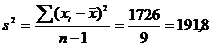 .
.
Testul statistic este:
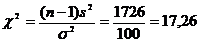 .
.
Cum 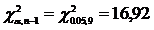 ,
,
si  vom respinge ipoteza
nula si vom accepta ipoteza alternativa,
vom respinge ipoteza
nula si vom accepta ipoteza alternativa,  .
.
Factorii ce identifica
testul  privind dispersia unei
populatii:
privind dispersia unei
populatii:
Obiectiv: caracterizarea unei
colectivitati;
Aspectul vital: variabilitatea;
Tipul datelor: cantitative.
TESTAREA IPOTEZEI PRIVIND
RAPORTUL DINTRE DOUA DISPERSII
Am vazut ca testarea ipotezei privind
dispersia poate fi utilizata pentru a trage concluzii referitoare la
consistenta unor procese economice ori privitoare la riscurile asociate.
In continuare vom compara doua dispersii, ceea ce ne va permite sa
comparam consistenta a doua procese sau riscurile a doua
portofolii de investitii etc.
Statisticienii testeaza, adesea, egalitatea
dintre doua dispersii inainte de a decide ce procedeu sa
foloseasca in verificarea ipotezei privind diferenta dintre doua
medii.
Vom compara dispersiile a doua populatii,
determinand raportul dintre ele. In consecinta, parametrul ce ne
intereseaza este 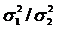 . Daca dispersia esantionului este (asa cum am
vazut) un estimator nedeplasat si consistent al dispersiei
colectivitatii generale, sa notam ca raportul
. Daca dispersia esantionului este (asa cum am
vazut) un estimator nedeplasat si consistent al dispersiei
colectivitatii generale, sa notam ca raportul  este estimator
punctual al raportului de dispersii
este estimator
punctual al raportului de dispersii 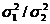 .
.
Distributia de esantionare a raportului  este o
distributie F, daca esantioanele au fost extrase independent din
populatii normal distribuite.
este o
distributie F, daca esantioanele au fost extrase independent din
populatii normal distribuite.
Valoarea lui F pentru care aria de sub curba
(situata la dreapta ei) este α, se noteaza cu Fα
(cu gradele de libertate gl1 si gl2).
Din matematica stim
ca raportul dintre doua variabile hi-patrat independente
impartite la gradele lor de libertate are o distributie F.
Gradele de libertate ale distributiei F sunt identice cu gradele de
libertate ale celor doua distributii hi-patrat. Atunci:
 ,
,
cu  si
si  grade de libertate.
grade de libertate.
In cele ce urmeaza, ipoteza nula este
intotdeauna specificata ca egalitatea intre doua dispersii,
adica sub forma egalitatii raportului cu unitatea.
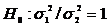 .
.
Ipoteza alternativa poate fi construita
astfel: fie ca raportul este diferit de 1, fie mai mare, fie mai mic decat
1.
Tehnic, testul statistic este  , dar in conditiile ipotezei nule, adica
, dar in conditiile ipotezei nule, adica  , testul statistic devine:
, testul statistic devine: 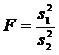 , care urmeaza o distributie F cu
, care urmeaza o distributie F cu  si
si  grade de libertate.
grade de libertate.
Regiunea critica este data de:
 sau
sau 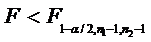 pentru test bilateral,
pentru test bilateral,
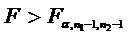 pentru test unilateral
dreapta,
pentru test unilateral
dreapta,
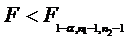 pentru test unilateral
stanga.
pentru test unilateral
stanga.
Trebuie facuta observatia ca:

unde:
Exemplu:
Un analist
doreste sa compare imprastierea veniturilor pe familie,
pentru colectivitatea turistilor ce prefera turismul litoral, cu
imprastierea veniturilor, pentru colectivitatea turistilor ce
prefera turismul balnear. Presupunand ca distributiile
veniturilor (mil. lei), in cele doua colectivitati sunt
aproximativ normale au fost selectate doua esantioane, de volum 60
si 50 de persoane, iar abaterile medii patratice (mil. lei) sunt:  si
si 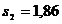 . Se utilizeaza o probabilitate de garantare a
rezultatelor de 95%.
. Se utilizeaza o probabilitate de garantare a
rezultatelor de 95%.
Ipotezele statistice sunt:
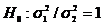 ,
,
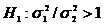 .
.
Testul statistic are valoarea:
 .
.
Regiunea critica (pentru 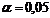 ) este data de:
) este data de:
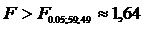 .
.
Cum 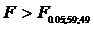 ipoteza nula se
respinge (aceea ca raportul dintre dispersii este 1) si se
accepta ipoteza alternativa. Acest lucru inseamna ca se
accepta ipoteza conform careia imprastierea veniturilor
pentru turistii din zona litorala este semnificativ mai mare decat
cea a turistilor din zona balneara.
ipoteza nula se
respinge (aceea ca raportul dintre dispersii este 1) si se
accepta ipoteza alternativa. Acest lucru inseamna ca se
accepta ipoteza conform careia imprastierea veniturilor
pentru turistii din zona litorala este semnificativ mai mare decat
cea a turistilor din zona balneara.
In general - daca la numarator se trece dispersia cea mai
mare - testul F este un test unilateral dreapta.



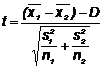
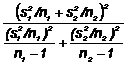
 .
.
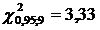
 ,
, , dar in conditiile ipotezei nule, adica
, dar in conditiile ipotezei nule, adica 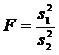 , care urmeaza o distributie F cu
, care urmeaza o distributie F cu 