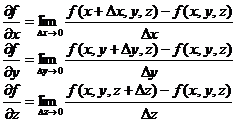Gradientul
unei functii scalare
Fie 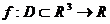 o functie
scalara oarecare de coordonate, continua si
diferentiabila.
o functie
scalara oarecare de coordonate, continua si
diferentiabila.
Cu ajutorul derivatelor ei partiale:
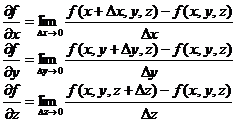 (A.4.1)
(A.4.1)
se poate construi in
fiecare punct din spatiul de definitie, un vector ale carui
componente sunt derivatele partiale respective. Acest vector se
numeste gradientul lui f si
se noteaza:
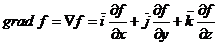 (A.4.2)
(A.4.2)
unde:
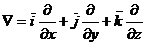 (A.4.3)
(A.4.3)
este operatorul vectorial diferential nabla,
iar 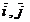 si
si 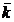 versorii axelor Ox, Oy
si respectiv, Oz.
versorii axelor Ox, Oy
si respectiv, Oz.
Gradientul unei functii intr-un punct este vectorul
a carui directie coincide cu directia de cea mai mare curbura
(raza este minima) si a carui marime este egala cu
panta masurata in aceasta directie. Directia
vectorului gradf intr-un punct
oarecare este directia care pornind de la acest punct permite
cresterea cea mai rapida a functiei f.
Produsul scalar dintre gradf si vectorul deplasare infinitezimala:
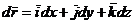 (A.4.4)
(A.4.4)
este diferentiala
functiei f:
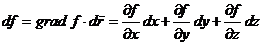 (A.4.5)
(A.4.5)