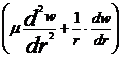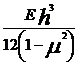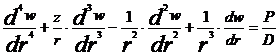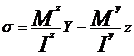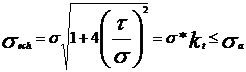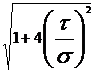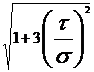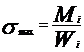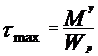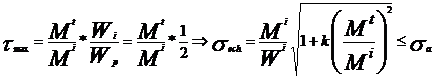CALCULUL MECANIC - POMPE CENTRIFUGE
1 Forta axiala la pompele centrifuge si metode de preluare a
acestora
In timpul functionarii pompelor centrifuge,
lichidul refulat de motor patrunde in spatiile
dintre acesta si stator, creand forte axiale ce tind sa
deplaseze ansamblul rotoric.
Forta
axiala ce actioneaza asupra ansamblului rotoric, ia
nastere, ca urmare a faptului ca in conditii normale de
functionare ( etansare normala intre rotor si stator)
presiunile ce actioneaza de o parte si de cealalta a
discului rotorului, pe portiunea BD nu sunt egale.

Fig. 1 Distributia presiunii lichidului in spatiile dintre
rotor si stator si notatiile corespunzatoare pentru
calculul fortei axiale.
In stanga, lichidul din interstitiul "2" dupa
laminare in dispozitivul de etansare comunica cu lichidul aspirat a
carei presiune este "P1". In dreapta, lichidul din
interstitiul "i" necomunicand cu cel aspirat va avea o presiune
diferita de presiunea "P1".
Pentru determinarea legii de variatie a presiunii
lichidului in cele doua interstitii 1 si 2 in general se fac
urmatoarele ipoteze simplificatoare:
la intrarea
lichidului in fantele 1 si 2 energia hidrostatica Hp este egala.
lichidul aflat intre rotor si stator este
antrenat intr-o miscare de rotatie cu o viteza unghiulara
egala cu semisuma vitezelor unghiulare a celor doua elemente,
adica:
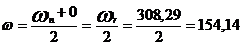 rad/s
rad/s
unde 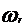 - viteza unghiulara a
rotorului
- viteza unghiulara a
rotorului
Pe portiunea
rotorului cuprinsa in zona BD presiunile nefiind egale apare o
forta rezultanta ce tinde sa deplaseze ansamblul rotoric
catre conducta de aspiratie.
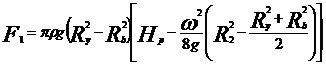
in care 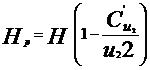 - inaltimea hidrostatica la iesirea
lichidului din rotorul cu numar finit de pale
- inaltimea hidrostatica la iesirea
lichidului din rotorul cu numar finit de pale
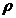 - masa specifica a
lichidului vehiculat
- masa specifica a
lichidului vehiculat
Ry, Rb - razele rotorului la nivelul
interstitiului de etansare si butucului.
Concomitent cu forta "F1"
in timpul functionarii pompelor centrifuge datorita
schimbarii directiei vinei de lichid la intrarea in rotor apare o
noua forta (F2).
Aceasta
forta poate fi calculata pe baza teoremei impulsului cu formula:
F2 ·Q·C0
La pompele centrifuge cu
arborele de antrenare orizontal, forta totala ce actioneaza
asupra ansamblului rotoric va fi data de suma celor doua forte:
Fr=F1+(-F2)
In situatia unor
pompe multietajate, ca urmare a uzurii elementelor de etansare dintre
etaje (diafragmelor), forta axiala se calculeaza inlocuind Ry cu
raza monsonului de protectie sau bucsei de fixare a rotorului pe
arbore.
Pentru
echilibrarea fortelor axiale, urmatoarele procedee sunt cele mai
raspandite:
a)
Dispunerea rotoarelor astfel incat fortele axiale
sa se echilibreze reciproc;
b)
Utilizarea dispozitivelor hidraulice de preluare
fortelor axiale.
Dispunerea
rotoarelor in pompa este posibila in mai
multe variante, fiecare varianta prezentand avantajele si
dezavantajele corespunzatoare.
Primul procedeu este
larg raspandit la pompele de procesdatorita sigurantei in
functionare si a unei exploatari usoare.
Acest procedeu consta in dispunerea
rotoarelor cu aspiratia intr-o parte si cealalta fiind usor
de utilizat la pompele centrifuge cu numar par de trepte. In situatia unui numar impar de trepte, pentru
utilizarea acestui procedeu, prima treapta se realizeaza cudublu
flux.
Folosirea
acestui procedeu pentru pompele centrifuge cu numar de trepte mai mare
decat patru conduce la dificultati de realizare.
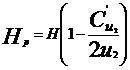
unde H=180 mcA
u2=42.79 m/s
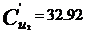 m/s
m/s 
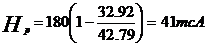
In cazul vehicularii titeiului Hp=65.11 m
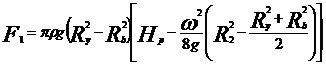
unde Ry=R0=58 mm
Rb=db/2=72/2=36
mm.
R2=138.5 mm.
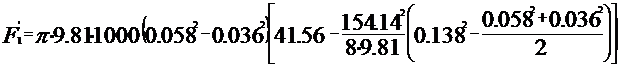
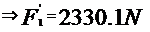
In cazul vehicularii titeiului :
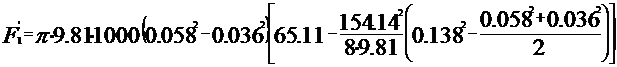
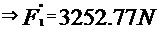
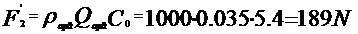
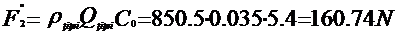
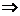
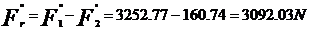
Deci forta axiala ce apare la pompa centrifuga prin
vehicularea titeiului va fi: Fa=3092,03 N
2 Calculul de alegere al rulmentilor
Reprezentarea in desen a
rulmentilor se face tinandu-se seama de regulile stabilite prin STAS
105-64 si STAS 188-64, cu respectarea formelor constructive si a
dimensiunilor prevazute in standardele pentru rulmenti. Modul de reprezentare
a rulmentilor in desenele de executie este stabilit prin STAS
8953-71.
Schema de incarcare a
rulmentilor este reprezentata in figura urmatoare:
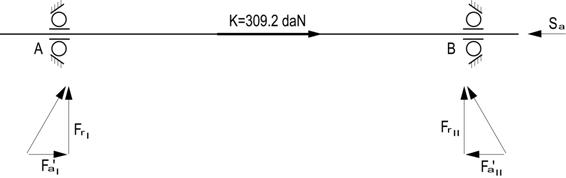
Fig. 2.1 Schema de incarcare a rulmentilor
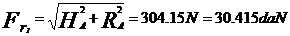
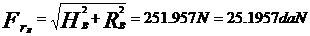 , unde FrI, FrII - fortele radiale
din rulmenti
, unde FrI, FrII - fortele radiale
din rulmenti
Fortele interioare axiale din rulmenti sunt:
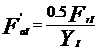
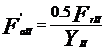
Forta axiala
K=309,2 daN
Se aleg rulmenti radiali- axiali cu bile pe un rand
care au diametrul interior d=50 mm
Pentru 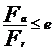 x=1; y=0; e=1.14; x0=0.5; y0=0.26
x=1; y=0; e=1.14; x0=0.5; y0=0.26
Pentru 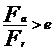 x=0.35; y=0.57; e=1.14;
x=0.35; y=0.57; e=1.14;
Avand urmatoarele caracteristici :
D mm. B=20 mm C=2750
daN
Sau
D=110 mm. B=27 mm C=4800 daN,
unde D este diametrul exterior al rulmentului, B este
latimea lui, C este capacitatea dinamica, C0=2000 daN
respectiv C0=3650 daN reprezinta capacitatea statica.
Comparatia caracteristicilor functionale ala principalelor tipuri
de rulmenti radiali axiali cu bile pe un rand:
capacitatea de
incarcare - radiala - buna (B); axiala - foarte buna(FB); combinata - foarte buna (FB);
turatia foarte buna; compensarea abaterilor de aliniere
nesatisfacatoare.
Se merge pe solutia constructiva ca
rulmentii sa fie identici pe cele doua reazeme.
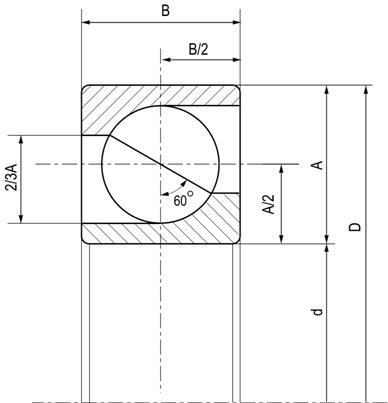
Fig. 2.2 Rulmentul radial axial
cu bile pe un rand.
Se calculeaza fortele axiale interioare:
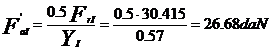
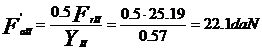
Se calculeaza fortele axiale din rulmenti,
observandu-se ca:
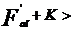

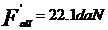
Rezulta ca
rulmentul (II) este cel mai incarcat. Pentru echilibru este necesar
sa se introduca o forta exterioara Sa
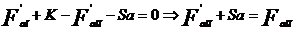 , deci
, deci
FaII= K+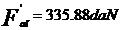
FaI=
Se fac rapoartele :
FaI/FrI=26.68/30.45=0.877 < e=1.14
FaII/FrII=335.88/25.19=13.33 > e=1.14
Calculul fortelor echivalente :
PI=(V·XI·FrI+YI·FaI)·Kt·Kd
PII=(V·XII·FrII+YII·FaII)·Kt·Kd
Se considera ca rulmentii lucreaza la o
temperatura mai mica de 1000C, iar coeficientul dinamic Kd=1,1..1,3
pentru socuri moderate, coeficientul de temperatura Kt=1. Se alege
Kd=1.3
V - coeficient ce tine seama de inelul care se roteste;
V=1 daca se roteste inelul interior
X - coeficient radial
Y - coeficient axial
Dupa valorile
rapoartelor 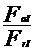 si
si 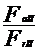 sarcinile echivalente sunt:
sarcinile echivalente sunt:
PI=V·XI·FrI·Kt·Kd=1·1·30.415·1·1.3=39.54 daN
PII=(V·XII·FrII+YII·FaII)·Kt·Kd=(1·0.35·25.19+0.57·335.88)01.3
PII=260.35
daN
Se calculeaza capacitatea
dinamica a rulmentilor cu:
P= max(pI;pII)=260.35 daN
L=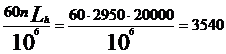 milioane rotatii
milioane rotatii
C=p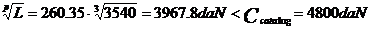
Deci
rulmentul este bine ales avand urmatoarele
caracteristici:
d=50 mm.
D=110 mm.
B=27 mm.
C=4800 daN
-capacitatea dinamica
C=3650 daN
- capacitate statica
Cu valorile din catalog se recalculeaza durabilitatea rulmentului : L=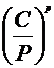 unde p=3 pentru rulmenti cu bile
unde p=3 pentru rulmenti cu bile
L=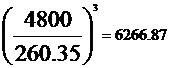 milioane rotatii
milioane rotatii
Iar durata de functionare Lh 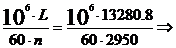 Lh=35406.04 ore
Lh=35406.04 ore
Capacele frontale pentru lagarele cu rulmenti se aleg in
functie de diametrul exterior D al rulmentului.
Astfel, pentru diametrul
D=110 mm vom alege un capac avand urmatoarele dimensiuni:
D1=170
mm b=12 mm
D2=140
mm d1=14
mm
D3=96
mm e=20 mm
numarul
de suruburi ns=6
dimensiunile
locasului garniturii
d=65 mm; D0=82 mm
d0=66 mm; b0=7 mm
Montajul rulmentilor
Se da o deosebita
atentie acestei operatii. Este
facuta de obicei de muncitorii cu calificare inalta.
Deosebita atentie se
da ajustajelor rulmentilor. La alegerea unui ajustaj este necesar
sa se evite marimea exagerata a strangerilor si jocurilor.
Strangerile prea mari pot produce spargerea rulmentului chiar in faza de
montaj. Jocurile prea mari dauneaza rigiditatii
asamblarii ducand la o uzura prematura in zona de contact.
2.2 Ungerea rulmentilor
Se face in scopurile:
Sa
micsoreze frecarea dintre partile componente in miscare
Sa
asigure protejarea anticoroziva a rulmentilor;
Sa
impiedice patrunderea impuritatilor din afara;
Sa
uniformizeze repartitia si cedarea de caldura;
Sa
micsoreze in anumite limite zgomotul produs de rulment.
O ungere corespunzatoare o asigura cresterea duratei de
functinare
a
rulmentului. Ungerea se face cu lubrifianti de buna calitate.
Lubrifiantii trebuie sa indeplineasca urmatoarele
conditii fundamentale:
Sa
aiba o stabilitate fizica si chimica;
Sa nu
contina elemente metalice;
Sa fie
substante neutre;
Sa fie
faar continut de acizi sau baze;
Sa
aiba continut mic de cenusa.
Lubrifiantii se impart in trei grupe:
a)
Lubrifianti
lichizi
b)
Lubrifianti
consistenti
c)
Lubrifianti
solizi.
3.1. Alegerea cuplajului
dintat
Legatura dintre arborele pompei
centrifuge si arborele motorului de antrenare este asigurata de un
cuplaj dintat care sa poata prelua abaterile axiale, radiale
si de rotire si sa poata transmite momente mari de
torsiune.
Alegerea cuplajului dintat se
face conform STAS 6589
Standardul se refera la
cuplajele mecanice permanente, compensatoare, de uz general, tip cuplaje
dintate, destinate cuplarii arborilor coaxiali cu capete conice lungi
cu filet interior, avand diametrul capatului de arbore de la 30 la 560 mm.
Tipuri si variante de
executie:
cuplajele se
executa in doua tipuri:
a)
cuplaj dublu
dintat, simbol CDD;
b)
cuplaj simplu
dintat, simbol CD.
Cuplajele simbol CD se executa in varianta s de baza,
pozitia de functionare H.
Dimensiunile cuplajului sunt:
dH7=45 mm d4h6=87 mm D1h8=155 mm
d1h0=14 mm dSr6=124 mm D2=140 mm
d0=15 44 mm d6filet=M8 D3=120 mm
44 mm d6filet=M8 D3=120 mm
d2=60 mm d7=60 mm D4=85 mm
d3=42.6 D=135 mm D5=124 mm
Db1=72 mm Db2=85 mm l=82 mm
l1=59 mm
Cuplajul poate functiona
pana la turatii nmax = 4500 rot/min si la un moment nominal Mn
= 1250 (Nm) avand masa Mc = 6.7kg si
momentul de inertie j = 0.068 kgm2.
Notarea unui cuplaj cuprinde:
a)
Denumirea
cuplajului si simbolul lui;
b)
Marimea
cuplajului;
c)
Simbolurile
variantei si pozitiei de functionare, urmate de o linie
orizontala;
d)
Simbolul
executiei, dupa caz, a unui butuc dintat sau a unei semicuple si valoarea diametrului
nominal al alezajului, urmat de o linie oblica;
e)
Simbolul
executiei, dupa caz, a celuilalt butuc dintat sau a celeilalte
semicuple, valoarea diametrului nominal al alezajului urmat de o linie
orizontala;
f)
Numarul
prezentului standard.
In cazul nostru cuplaj CD = SH-CMI 45/Ki50 - STAS 6589/2-81
Cuplajele se aleg in functie de diamtetrele capetelor de arbori pe
care
ii cupleaza si in functie de momentul de
lucru M8 necesar de transmis.
Verificarea prin calcul a cuplajelor
se face cu ajutorul relatiei:
Mn
>= Me
in care
Mn momentul nominal (Nm)
Me - mom entul de lucru necesar de transmis determinat prin relatia:
Me = Mc Cs in care
Mc - momentul de calcul
determinat prin relatia:
Mc = 9550·N/n, unde
N - puterea necesara;
N (CP)
n turatia
arborelui
n = 2950 rot/min
Cs = coeficient de
serviciu, se alege in functie de tipul masini antrenoare si de
regimul de lucru al masinii antrenate.
Cs = 1.12
A = Mmax/Mn <=
1,8
Mc=9550· [Nn]
[Nn]
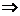 Mc=1.12 1080.98=1210.69 Nn
< Mn=1250Nn
Mc=1.12 1080.98=1210.69 Nn
< Mn=1250Nn
Butucii dintati se
executa dupa cum urmeaza:
a)
pregauriti - executie P
b)
cu alezaj la
diametru nominal (la cerere)
executie C, cu alezaj cilindric
executie Ki cu
alezaj conic.
Butucii
dintati in executie P si C sunt destinati pentru toate
marimile de cuplaj pentru marimea cuplajului 2:
l2
= 60mm; l3 = 60mm
Cuplajele
dintate sunt alcatuite din: doi butuci danturati exterior, un manson cu doua bucati, cu flanse
asamblate prin suruburi de fixare; capace frontale cu garnituri de
pasla care impiedica scurgerea lubrifiantului.
Dintii celor
doua semicuple cu profilul in evolventa modificat prin bombare
si deplasare.
Asamblarea semicuplajelor pe capetele
arborilor se face prin pene paralele. Pentru reducerea
fortelor de frecare pe dinti, cuplajele se executa cu
dintii durificati si se ung cu ulei de vascozitate mare.
Avantaje:
capacitate mare de transmitere a momentelor de torsiune la dimensiuni da
gabarit reduse si turatii relativ mari.
Butucii dintati se
executa din otel marca 34 Mo Cr Ni 15, semicuplele din 0T60-3,
materiale din care se executa si celelalte elemente componente ale
cuplajului, conform documentatiei de executie.
3.2. Calculul penelor
Penele sunt organe de asamblare
demontabile, cu forma in general apropiata de prisma, cu
sectiune constanta sau cu una din fete inclinata. Dupa
pozitia lor fata de axa pieselor asamblate si dupa
rolul functional, se deosebesc doua mari categorii:
a)
Pene transversale, care se monteaza perpendicular
pe axa pieselor, respectiv pe directia sarcinii, ele sunt totdeauna
prevazute cu inclinare;
b)
Pene
longitudinale - cu sau fara inclinare - care se monteaza paralel
cu axa geometrica a pieselor de solidarizat (arbore - butuc) si
transmit momente de torsiune.
Dupa forma lor si
dupa functionarea organelor de asamblat, penele longitudinale
asigura legatura dintre butuc si arbore, prin strangere -
realizand numai transmiterea momentelor de torsiune; sau fara
strangere - in paralel cu transmiterea acestor momente, permitand
deplasarea axiala a piesei montate pe arbore.
Penele longitudinale sunt montate
paralel cu axa arborelui, intr-un canal prelucrat fie numai in butuc -
forma speciala - fie partial in butuc si partial in
arbore - cazul general. Penele paralele cu sectiunea dreptunghiulara
constanta pe intreaga lor lungime, fiind lipsite de inclinare. Ca principiu ele sunt pene de antrenare, fara
strangere, transmiterea momentului facandu-se prin presiunea
exercitata de butuc si arbore pe fetele lor laterale. Penele
paralele pot avea capetele drepte sau rotunde. La acestea din urma,
canalul are exact forma penei.
Asemenea pene sunt intrebuintate,
de obicei, cand se cere posibilitatea de deplasare axiala a butucului pe
arbore, ceea ce implica realizarea asamblarii cu un ajustaj
alunecator.
Pentru asigurarea contactului cu butucul
in orice pozitie, pana fiza in arbore capata lungimea
determinata de cursa butucului.
Neavand actiunea de ovalizare a
butucului, uneori penele sunt folosite si pentru fizare, ceea ce
implica un ajustaj fortat.
Prin apasarea laterala,
exista tendinta de smulgere a penei din canalul arborelui,
conjugata cu cresterea presiunilor de contact. Pentru preantampinarea
acestui neajuns, ca si pentru retinerea penei in pozitia ei,
cand butucul este mobil, se aplica masura constructiva de fixare
a penelor paralele in arbore cu unul sau doua suruburi.
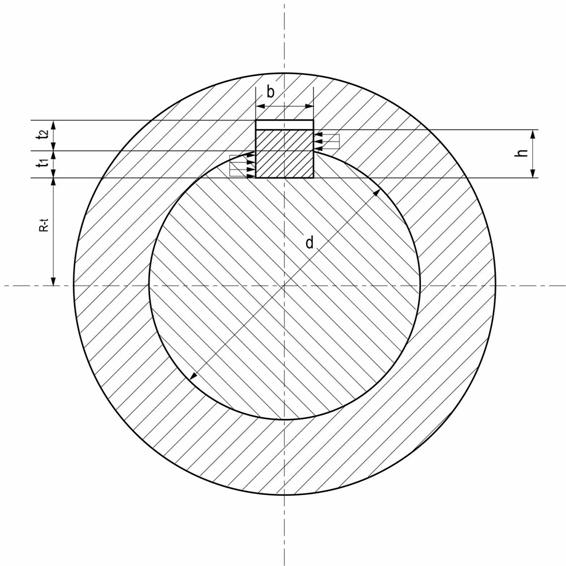
Fig. 3.2.1, Asamblare cu pana paralela
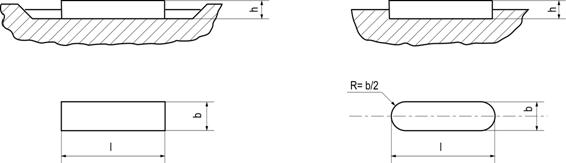
Fig. 3.2.2. Fig. 3.2.3.
Fig. 3.2.2. Pana
paralela cu capete drepte
Fig.
3.2.3. Pana
paralela cu capete rotunde
Prezenta gaurilor in arbore micsoreaza
resistenta lui la oboseala, deci folosirea suruburilor
trebuie limitata la cazurile strict necesare.
Penele longitudinale se executa din
oteluri de buna calitate, cu rezistenta de rupere de 50 ÷ 60
daN/mm , mai rar din
oteluri aliate.
Canalele din butuc se obtin prin
mortezare sau, daca numarul de piese justifica costul sculei,
prin brosare.
Canalul arborelui se frezeaza, de
obicei, cu freza disc pentru penele cu capete drepte si cu freza degetm,
pentru cele cu capete rotunde.
Toate penele longitudinale au muchiile
tesite, iar canalele au peretii racordati cu fundul (pentru
micsorarea efectului de concentrare); marimea tesiturilor
si razelor de racordare este prescrisa prein STAS 1004-59 si
STAS 1007-59.

Figura 3.2.4. Efectul
prezentei canalului de pana in cazul solicitarilor de: a)
inconvoiere; b) torsiune.
Alegerea
penelor se face conform STAS 1004-71 si STAS 1005-71
pentru
diametrul arborelui d = 45 mm se alege pana paralela avand dimensiunile:
b = 14 mm; h = 9 mm.
dimensiunile canalului:
in arbore t1
= 5,5 mm,
in butuc t
= 3,8 mm,
raza rmax = 0,25 mm.
Pentru
diametrul arborelui d = 60 mm se alege pana paralela avand dimensiunile:
b = 18 mm; h = 11 mm.
dimensiunile canalului:
in arbore t1
= 7 mm,
in butuc t
= 4,4 mm,
raza rmax = 0,25 mm.
Lungimile nominale sunt date in STAS 1005-71.
Presiunile
de contact admisibile pentru pana paralela utilizata pentru fixare
supuse actiunii unor sarcini fara socuri, au valori Pa =
800 . 1.500 kgf/cm
≈ 800 . 1.500 daN/cm ,
dupa materialul butucului (valorile minime se adopta pentru butucii
din fonta), iar daca butucul are deplasare axiala presiunile
admisibile se reduc la Pa = 100 . 300 daN/cm .
Se adopta o presiune
admisibila de contact pentru pana paralela utilizata pentru
fixare, de Pa = 120 N/mm ,
rezultand lungimea l'
a penei.
 mm.
mm.
Se adopta conform STAS 1005-71 o
lungime a penei l = 90 mm.
Pentru fixarea rotoarelor pe arbore se
alege o pana paralela conform STAS 1004-71 pentru diametrul d = 60
mm.
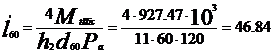 mm.
mm.
Se adopta conform STAS 1005-71 o
lungime a penei l = 50 mm.
4.1 Calculul diafragmei
Calculul diafragmei se face considerand-o placa plana
inelara incastrata pe conturul exterior si libera pe
conturul interior, incarcata cu o sarcina uniform
distribuita.
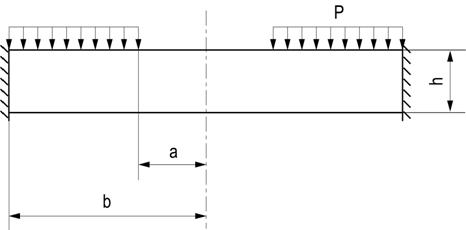
Fig. 4.1.1 Elementele geometrice
ale difragmei si repartitia sarcinii.
Dimensiunile placii plane (diafragmei) sunt:
a 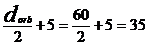 mm,
mm,
b 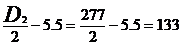 mm.
mm.
Se considera cazul placilor
circulare plane incarcate cu sarcini normale P = p(r), repartizate uniform
si rezemate continuu pe contururi circulare. Ca urmare, datorita
simetriei incarcarii si rezemarii, pe elmentul de placa rd dr vor apare numai tensiuni normale r in directia razei), (in directia tangenta) si tensiunea
tangentiala pe suprafata cu vector de orientare 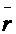
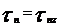 in directia Z,
normala la planul placii.
in directia Z,
normala la planul placii.
Prin ipoteza , se admite ca planele
paralele cu suprafata mediana nu se apasa intre ele si deci
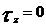
Reducand tensiunile de pe fiecare
fata a elementului, in raport cu centrul de greutate al fetei se
obtin eforturile sectionale:
Mr=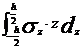
M 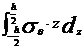 (1)
(1)
T=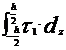
unde Z reprezinta distanta
unui plan oarecare fata de planul median al placii.
Din punct de vedere dimensional, Mr, M se exprima in N m/m iar T in
N/m.
Determinarea
tensiunilor si deplasarilor se face prin studiul celor trei aspecte:
geometric, fizic si satatic.
Aspectul
geometric: se admite:
a)
indeformabilitatea suprafetei mediane in planul
ei, in baza careia punctele O si O de pe
suprafata mediana din figura urmatoare se gasesc pe
verticalele lor,
b)
ipoteza normalelor drepte, care presupune ca
toate punctele de pe normala Δ se gasesc dupa
deformare pe dreapta Δ , normala pe suprafata mediana
deformata,
c)
ipoteza
micilor deplasari pe baza careia 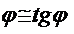
notand cu w deplasarea in directia normalei la planul
placii (axa z) din analiza aspectului geometric, rezulta:
 (2)
(2)
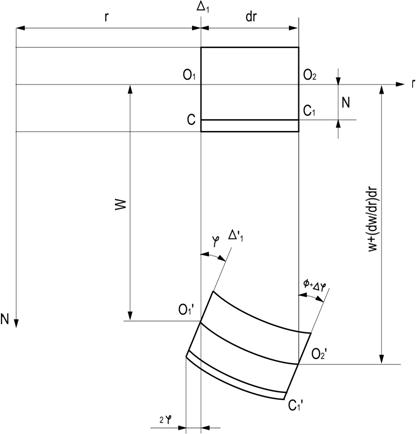
Fig. 4.1.2. Indeformabilitatea
sectiunii mediane.
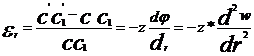 (3)
(3)
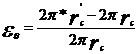 =-z·
=-z·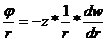 (4)
(4)
Aspectul fizic. Intrucat 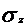 = 0, legea generalizata a
lui Hooke pentru directiile ortogonale r
si
= 0, legea generalizata a
lui Hooke pentru directiile ortogonale r
si 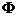 are forma:
are forma:
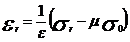 (5)
(5)
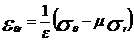 (6)
(6)
Explicitand din aceste relatii (5)
si (6) pe 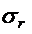 si
si 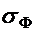 si tinand seama de relatiile
(2), (3), (4) se obtin tensiunile in functie de w:
si tinand seama de relatiile
(2), (3), (4) se obtin tensiunile in functie de w:
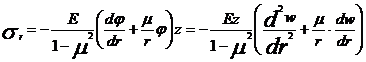 (7)
(7)
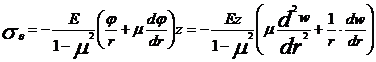 (8)
(8)
Prin introducerea acestor relatii in (1)
rezulta:
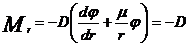
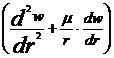 (9)
(9)
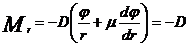
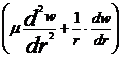 (10)
(10)
unde prin D s-a notat rigiditatea cilindrica a
placii.
D=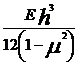 (11)
(11)
Aspectul static: se izoleaza
elementul de placa al suprafetei mediane si se introduc
eforturile sectionate corespunzatoare si se scriu ecuatiile
de echilibru.
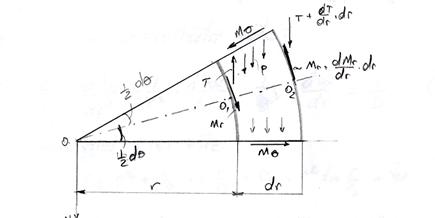
Fig. 4.1.3. Eforturile
sectionate in elementul de placa al suprafetei mediane.
Datorita
simetriei, din cele trei ecuatii de echilibru posibile raman
distincte numai doua:
- ecuatia de proiectie pe axa z.
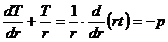 (12)
(12)
- ecuatia de
momente fata de tangenta din O
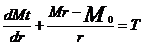 (13)
(13)
Ecuatia
diferentiala a rotirilor si a
sagetilor.
Introducand
in (13) expresiile (9) si (10) se obtine ecuatia
diferentiala a rotirii:
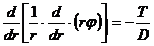 (14)
(14)
Daca
T din (14) si 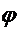 din (2) se inlocuiesc
in (12) se obtine ecuatia diferentiala a
sagetii w:
din (2) se inlocuiesc
in (12) se obtine ecuatia diferentiala a
sagetii w:
 (15)
(15)
a carei forma dezvoltata este:
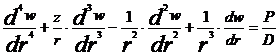 (16)
(16)
Solutia energiei este:
w1=c1+c2 r2+c3 ln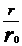 +c4 r2 ln
+c4 r2 ln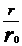
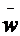 (17)
(17)
Pentru sarcini uniform distribuite
solutia particulara este:
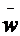 =
=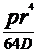 (18)
(18)
Calculul greutatii rotorului
Pentru calculul greutatii
rotorului, se va adopta o forma constructiva simplificata ca in
figura de mai jos:
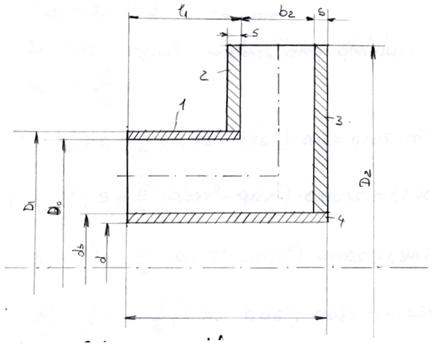
Fig. 4.2.1 Schema simplificata a rotorului
b mm = o,oo748 m
D = 122 mm =
0,122 m
D = 277 mm =
0,277 m
D = 116 mm =
0,116 m
db
= 72 mm = 0,072 m
d = 60 mm = 0,060 m
s = 3
mm = 0,0035 m
l = 10 mm =
0,01 m
l = 35 mm =
0,035m
mrot=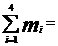 m1+m2+m3+m4
m1+m2+m3+m4
Greutatea rotorului Grot=mrot·g
unde: mrot=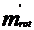 +
+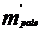 [kg] - masa
rotorului,
[kg] - masa
rotorului,
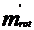 - masa
rotorului fara a lua in consideratie palele,
- masa
rotorului fara a lua in consideratie palele,
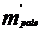 -
- 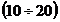 %·
%·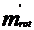 = masa palelor rotorice,
= masa palelor rotorice,
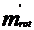 =
=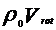 , in care:
, in care:
 kg/m3
kg/m3
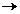 densitatea otelului.
densitatea otelului.
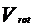 =
= ,
,
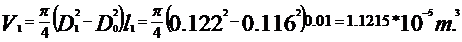
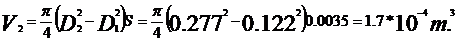

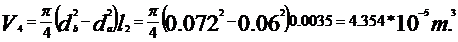
Vrot=V1+V2+V3+V4=4.214·10-4
m3
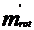 =7850·4.214·10-4=3.308 kg
=7850·4.214·10-4=3.308 kg
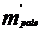 =
=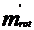 ·0.15=0.496 kg
·0.15=0.496 kg
Deci: mrot=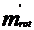 +
+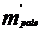 =3.308+0.496=3.8 kg
=3.308+0.496=3.8 kg 
Grot=
mrot·g=3.8·9.81=3278 N
Rotorul pompei centrifuge se va realiza din FC.200
prin turnare si va avea urmatoarele caracteristici conform STAS
568-82:
- rezistenta la
tractiune 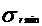 =Rmin=280 N/mm2
=Rmin=280 N/mm2
- rezistenta la incovoiere Ri=410 N/mm2
- sageata de
incovoiere 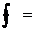 2 mm.
2 mm.
- duritatea Brinell
HB=170 210
210
Arborele
pompei centrifuge
Energia mecanica se transmite la
rotoul pompei centrifuge de la motorul de antrenare prin intermediul arborelui.
Arborele este de forma
cilindrica, de dimensiuni variabile, ce are
prevazute locasuri de pana pentru fixarea rotoarelor.
Asezarea arborelui pe reazeme se
poate face prin lagare cu cuzineti de bronz sau de cele mai multe ori
pe rulmenti.
Una din extremitati se prevede
cu cuplaje elastice pentru realizarea legaturii la motorul de antrenare.
Arborele pompei se va realiza din OLC 60
conform STAS 880-86.
|
Marca
otelului
|
Calitatea
|
Compozitia
chimica
|
|
C
|
Mn
|
S
|
P
|
|
OLC
60
|
s
|
0,57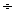 0,65 0,65
|
0,5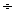 0,8 0,8
|
Max
0,045
0,020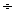 0,045 0,045
|
Max
0,04
|
|
X
xs
|
Max
0,035
0,020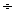 0,040 0,040
|
Max
0,035
|
Tabel 5.1 Compozitia chimica a
otelului carbon de calitate pentru tratament termic (STAS 880-86)
Observatie: Simbolurile S si X
semnifica: S - otel cu continut controlat de sulf; X - otel
carbon de calitate superior.
Caracteristicile mecanice ale
otelului carbon de calitate pentru tratament termic conform STAS 880-86
sunt:
-
limita de curgere 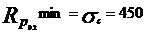 N/mm2
N/mm2
- rezistenta la rupere Rm 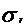
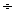 880 N/mm2
880 N/mm2
- alungirea la rupere Amin=14%
rezistenta
la rupere la un ciclu alternant simetric
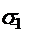 =350 N/m2
=350 N/m2
- efortul de forfecare la un
ciclu alternant simetric 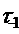 =200 N/m2
=200 N/m2
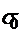 =380 N/mm2- pentru un
ciclu pulsator.
=380 N/mm2- pentru un
ciclu pulsator.
- Valorile sunt garantate numai
pentru tipul 4 de livrare
- Limita superioara a
rezistentei la rupere Rm se garanteaza numai la otelurile carbon
superioare cu continut controlat de sulf.
- Tratamentul termic este de
imbunatatire (calire + revenire inalta)
Arborele pompei este solicitat la
incovoiere cu torsiune.
Se va cerceta punctul cel mai solicitat
al sectiunii in care dezvolta atat tensiuni normale cat si
tangentiale. Dimensionarea se face dupa una din teoriile de
rezistenta. Singurele cu valabilitate sunt:
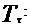
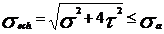
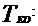
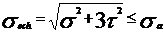
in care :
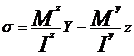
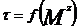
Conditia de rezistenta 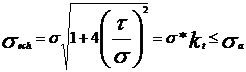
in care 
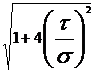
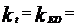
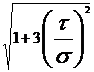
Aceasta
conditie de rezistenta se poate transforma intr-o formula
de dimensionare in toate cazurile in care 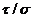 este
independent de parametrul geometric care defineste sectiunea (in
cazul sectiunilor dreptunghiulare, circulare sau unele casetate).
este
independent de parametrul geometric care defineste sectiunea (in
cazul sectiunilor dreptunghiulare, circulare sau unele casetate).
In
cazul nostru al sectiunii circulare:
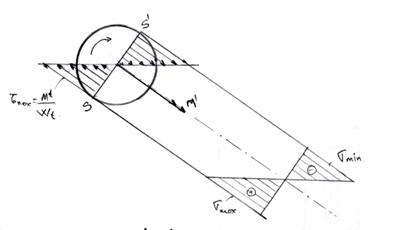
Fig. 5.2. Distributia de
tensiuni intr-o sectiune transversala a arborelui
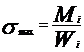 , unde
, unde
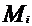 - momentul de incovoiere;
- momentul de incovoiere;
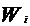 - modulul
de rezistenta la incovoiere;
- modulul
de rezistenta la incovoiere;
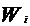
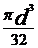 [mm3]
[mm3]
d -
diametrul arborelui [mm]
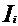
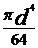 [mm4] - momentul de inertie axial
[mm4]
[mm4] - momentul de inertie axial
[mm4]
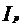
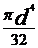 [mm4] - momentul de inertie polar
[mm4]
[mm4] - momentul de inertie polar
[mm4]
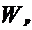 =
=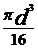 =2
=2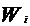 - modul de rezistenta polar
- modul de rezistenta polar
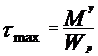
Mz - moment de torsiune.
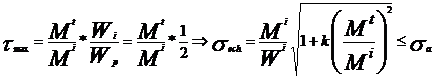
unde: k = 1 daca adoptam teoria 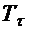
k daca
adoptam teoria TED
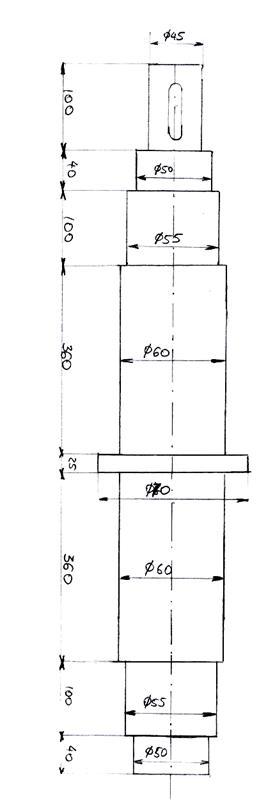
Fig. 5.3. Arborele pompei centrifuge



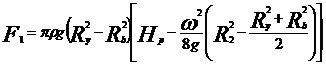
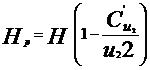 - inaltimea hidrostatica la iesirea
lichidului din rotorul cu numar finit de pale
- inaltimea hidrostatica la iesirea
lichidului din rotorul cu numar finit de pale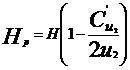
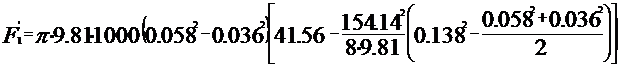
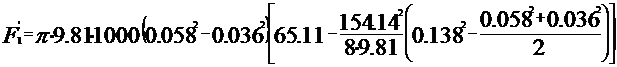

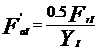
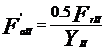
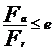
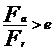

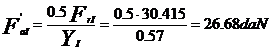
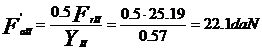
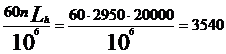
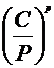 unde p=3 pentru rulmenti
unde p=3 pentru rulmenti 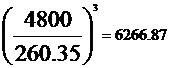 milioane rotatii
milioane rotatii



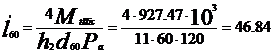

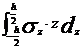
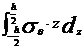
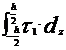

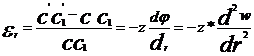 (3)
(3)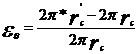 =-z·
=-z·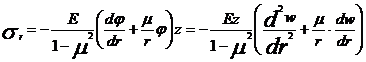
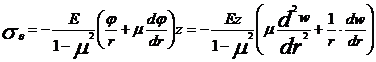
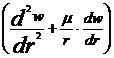 (9)
(9)