Inele principale
Definitia
1. Vom numi un inel principal sau
inel cu ideal principal un inel integru in care orice ideal este principal.
Din aceasta definitie
rezulta ca cprpurile comutative sunt inele principale. De asemenea,
inelul intregilor Z este un inel principal. Urmatoarea teorema ne
da posibilitatea sa dam si alte exemple de inele principale.
Teorema
2. Un inel euclidian este principal.
Demonstratie. Demonstratia
acestei teoreme este o generalizare fireasca a demonstratiei faptului
ca Z este inel principal (v cap II, 2 si cap. III). Fie A un inel
euclidian 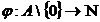 functia
respectiva si I un ideal in A. Vom arata ca I este ideal
principal. Daca I=(0), afirmatia este evidenta. Daca I
functia
respectiva si I un ideal in A. Vom arata ca I este ideal
principal. Daca I=(0), afirmatia este evidenta. Daca I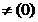 ,
consideram submultimea
,
consideram submultimea 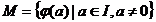 al lui N. Deoarece N este o multime
bineordonata, rezulta ca exista un element b
al lui N. Deoarece N este o multime
bineordonata, rezulta ca exista un element b I, b
I, b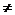 0 astfel ca
0 astfel ca (b) sa fie elementul minimal in M. Vom arata
ca bA=I. Incluziunea
(b) sa fie elementul minimal in M. Vom arata
ca bA=I. Incluziunea 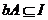 este evidenta,
deoarece b
este evidenta,
deoarece b I si I este ideal in A. Reciproc, fie a
I si I este ideal in A. Reciproc, fie a I. Deoarece b
I. Deoarece b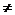 0, existp q,r
0, existp q,r  A astfel ca a=bq+r, unde r=0 sau
A astfel ca a=bq+r, unde r=0 sau  (r) <
(r) < (b). Va fi suficient sa observam ca r=0,
ca atunci a
(b). Va fi suficient sa observam ca r=0,
ca atunci a bA. Daca r
bA. Daca r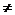 0, atunci din faptul ca r=a-bq
0, atunci din faptul ca r=a-bq I si
I si  (r) <
(r) < (b) rezulta o contradictie cu alegerea lui b.
(b) rezulta o contradictie cu alegerea lui b.
Din
aceasta teorema rezulta ca inelul intregilor lui Gauss 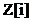 , inelul
, inelul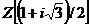 si orice inel de
polinoame de o nedeterminata cu coeficienti intr-un corp sunt inele
principale, fiindca acestea sunt inele euclidiene . Urmatoarea
propozitie ne permite sa dam exemple de inele care nu sunt
principale.
si orice inel de
polinoame de o nedeterminata cu coeficienti intr-un corp sunt inele
principale, fiindca acestea sunt inele euclidiene . Urmatoarea
propozitie ne permite sa dam exemple de inele care nu sunt
principale.
Propozitia
Fie A un inel integru care nu este
corp. Atunci inelul polinoamelor de o nedeterminata cu A[X] nu
este inel principal.
Demonstratie. Din faptul
ca A nu este corp rezulta ca exista un element a A,
a
A,
a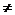 0 si a neinversabil. Sa aratam
ca idealul generat de a si X nu este principal. Sa presupunem
ca a A[X] +XA[X]=(f),
cu f
0 si a neinversabil. Sa aratam
ca idealul generat de a si X nu este principal. Sa presupunem
ca a A[X] +XA[X]=(f),
cu f A. Atunci din a=fg cu g
A. Atunci din a=fg cu g A[X] rezulta ca f
A[X] rezulta ca f A, iar din faptul ca X=fg', g'
A, iar din faptul ca X=fg', g' A[X], rezulta ca
f este inversabil in A si deci rezulta ca A[X]
+XA[X]= A[X] . De aici rezulta relatia 1=a
A[X], rezulta ca
f este inversabil in A si deci rezulta ca A[X]
+XA[X]= A[X] . De aici rezulta relatia 1=a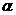 +X
+X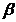 , cu a,b
, cu a,b A[X],
relatie imposibila caci
A[X],
relatie imposibila caci 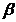
 0,
fiindca a nu este inversabil.
0,
fiindca a nu este inversabil.
Din
aceasta propozitie rezulta ca Z[X] nu este inel
principal si orice inel de polinoame de n>1
nedeterminate cu coeficienti intr-un corp nu este inel principal si
deci nici euclidian.
Vom demonstra acum cateva
proprietati aritmetice ale inelelor principale.
Propozitia
4. Fie A un inel principal si a,b A.
Atunci:
A.
Atunci:
i)
Elementul
d A este cel mai mare divizor comun al elementelor a
si b daca si numai daca Aa+bB=dA.
A este cel mai mare divizor comun al elementelor a
si b daca si numai daca Aa+bB=dA.
ii)
Elementul
m A este cel mai mic multiplu comun al elementelor a
si b daca si numai daca mA=
A este cel mai mic multiplu comun al elementelor a
si b daca si numai daca mA=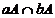 .
.
Demonstratie. i) Daca d A
este cel mai mare divizor comun al elementelor a si b, atunci avem evident
a
A
este cel mai mare divizor comun al elementelor a si b, atunci avem evident
a dA, b
dA, b dA si deci aA+bA
dA si deci aA+bA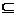 dA. Insa aA+bA este ideal principal, deci aA+bA=d'A.
Atunci rezulta d' divizor comun al lui a si b, deci d' divide pe d,
adica d'A= aA+bA
dA. Insa aA+bA este ideal principal, deci aA+bA=d'A.
Atunci rezulta d' divizor comun al lui a si b, deci d' divide pe d,
adica d'A= aA+bA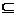 dA. Reciproc, daca d
dA. Reciproc, daca d A
este astfel incat aA+bA=dA, atunci evident d este divizor comun al lui a
si b si in plus exista relatia d= a
A
este astfel incat aA+bA=dA, atunci evident d este divizor comun al lui a
si b si in plus exista relatia d= a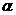 +b
+b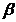 , cu a,b
, cu a,b A
din care rezulta ca orice divizor comun al lui a si b divide pe
d.
A
din care rezulta ca orice divizor comun al lui a si b divide pe
d.
ii)
Daca m este cel mai mic multiplu comun al elementelor a si b, atunci
evident mA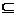
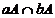 .
Insa idealul
.
Insa idealul 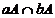 este principal,
deci
este principal,
deci 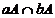 =m'A si deoarece m' este evident multiplu comun al
elementelor a si b, rezulta ca m divide pe m', adica mA
=m'A si deoarece m' este evident multiplu comun al
elementelor a si b, rezulta ca m divide pe m', adica mA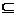 m'A=
m'A=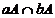 , si deci egalitatea ceruta.
, si deci egalitatea ceruta.
Reciproc,
daca m  A este astfel ca mA=
A este astfel ca mA=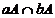 , atunci m este un multiplu comun al lui a si b.
Fie m' alt multiplu comun al lui a si b; atunci m'
, atunci m este un multiplu comun al lui a si b.
Fie m' alt multiplu comun al lui a si b; atunci m' A si m'
A si m' bA, deci m'A
bA, deci m'A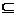
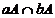 =mA, deci m divide pe m'.
=mA, deci m divide pe m'.
Asadar
intr-un inel principal A idealul generat de un numar finit de elemente 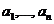 coincide cu idealul generat de cel mai mare divizor
comun al acestor elemente. De aici provine notatia (
coincide cu idealul generat de cel mai mare divizor
comun al acestor elemente. De aici provine notatia (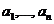 ); utilizata atat pentru c.m.m.d.c al elementelor
); utilizata atat pentru c.m.m.d.c al elementelor 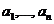 cat si
pentru idealul generat de aceste elemente.
cat si
pentru idealul generat de aceste elemente.
Corolarul 5. Intr-un inel principal
orice doua elemente au cel mai mare divizor comun si cel mai mic
multiplu comun, iar daca d A este cel mai mare divizor comun al elementelor a
si b din A, atunci exista
A este cel mai mare divizor comun al elementelor a
si b din A, atunci exista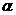 ,
,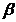
 A
astfel ca d=
A
astfel ca d= 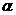 a+
a+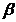 a.
a.
Din acest corolar si din
propozitia 1.15 rezulta:
Corolarul 6. Intr-un inel principal
orice element ireductibil este prim. Din acest corolar deduce ca inelul 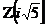 nu este inel principal.
nu este inel principal.
Teorema 7. Intr-un inel principal
orice element nenul si neinversabil se descompune in produs finit de
elemente prime.
Demonstratie. Deoarece orice
element ireductibil este prim in inelele principale (corolarul precedent), este
suficient sa aratam ca orice element nenul este produs de
elemente ireductibile. Vom demonstra prin reducere la absurd, adica vom
presupune ca exista in inelul A un element nenul si neinversabil
a care nu este produs finit de elemente ireductibile si vom ajunge la o contradictie.
In adevar, a nu poate fi ireductibil, deci exista o descompunere a
lui de forma a= 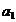
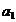 ', in care
', in care 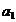 si
si 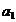 ' nu sunt asociati cu a si sunt elemente
neinversabile si nenule. Este clar ca atunci cel putin unul
dintre elemetele
' nu sunt asociati cu a si sunt elemente
neinversabile si nenule. Este clar ca atunci cel putin unul
dintre elemetele 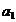 si
si 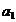 ' are proprietatea lui a, adica nu este produs
finit de elemente ireductibile (caci altfel a ar fi produs finit de
elemente ireductibile impotriva ipotezei). Rationand analog cu
' are proprietatea lui a, adica nu este produs
finit de elemente ireductibile (caci altfel a ar fi produs finit de
elemente ireductibile impotriva ipotezei). Rationand analog cu 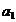 , gasim un divizor
, gasim un divizor 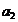 lui
lui 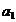 , care este neinversabil si neasociat cu
, care este neinversabil si neasociat cu 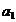 si care are
aceeasi proprietate s.a.m.d. Se obtine astfel un sir infinit de
elemente neinversabile din A:
si care are
aceeasi proprietate s.a.m.d. Se obtine astfel un sir infinit de
elemente neinversabile din A:
a= 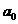 ,
, 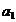 ,
, 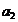 , . ,
, . ,
cu proprieatatea 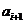 divi pe
divi pe 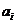 si nu este asociat cu acesta, i=0,1, . Din acest
sir rezulta strict crescator infinit ideale ale inelului A:
si nu este asociat cu acesta, i=0,1, . Din acest
sir rezulta strict crescator infinit ideale ale inelului A:
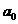 A
A
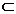
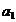 A
A 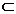
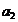 A
A 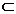
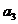 A
A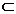 .
.
Lema urmatoare arata insa ca
un astfel de sir nu poate exista intr-un inel principal.
Lema 8. Fie A un inel principal si
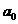 A
A
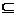
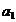 A
A 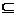
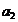 A
A 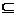 .
.
un sir crescator infinit de ideale din
A. Exista atunci n>0 astfel ca 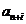 A=
A=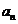 A pentru orice i
A pentru orice i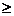 0
0
Demonstratie. Fie 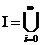
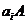 .
Atunci I este ideal in A, caci daca b,c
.
Atunci I este ideal in A, caci daca b,c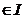 , atunci exista i,j
, atunci exista i,j 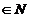 astfel
ca b
astfel
ca b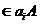 , iar daca k=max(i,j), atunci b,c
, iar daca k=max(i,j), atunci b,c 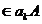 . Deoarece
. Deoarece 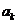 A este ideal, rezulta
A este ideal, rezulta
b-c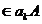 si pentru orice
si pentru orice 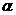
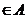 , ab
, ab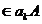 , deci b-c
, deci b-c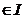 si a,b
si a,b 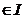 . Inelul A fiind principal, exista
. Inelul A fiind principal, exista 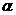
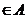 astfel ca I=aA.
Cum a
astfel ca I=aA.
Cum a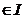 , rezulta ca exista un numar
natural n astfel ca a
, rezulta ca exista un numar
natural n astfel ca a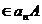 . Atunci deduce aA
. Atunci deduce aA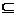
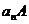 si din incluziunile
si din incluziunile 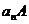
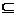
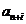 A
A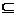 aA, pentru i
aA, pentru i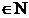 , se deduce afirmatia lemei.
, se deduce afirmatia lemei.
In
incheierea acestui paragraf sa observam ca in demonstratia
faptului ca orice inel euclidian este principal am folosit din
definitia inelelor euclidiene numai proprietatea ii), adica teorema
impartirii intregi. S-ar putea crede ca aceasta proprietate
este eventual satisfacuta de o clasa mai larga de inele.
Propozitia urmatoare arata insa ca in definitia
inelelor euclidiene este esentiala numai proprietatea ii).
Propozitia 9. Fie A un inel
integru si 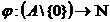 o functie
care are proprietatea ii) din definitia 2.1. Atunci functia
o functie
care are proprietatea ii) din definitia 2.1. Atunci functia 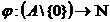 , definita prin
, definita prin
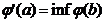
cand b parcurge toate elementele asociate cu a,
satisface i) si ii) si din aceeasi definitie.
Demonstratie. Vom verifica mai
intai ca  '
satisface pe ii). Fie a si b elemente din A, b
'
satisface pe ii). Fie a si b elemente din A, b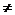 0 si b' un element asociat cu b pentru care
0 si b' un element asociat cu b pentru care  '(b)=
'(b)=  (b'). Atunci evident b'
(b'). Atunci evident b'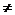 0 deoarece
0 deoarece  satisface ii),
rezulta ca exista q si r astfel ca a=b'q+r, cu r=0 sau
satisface ii),
rezulta ca exista q si r astfel ca a=b'q+r, cu r=0 sau  (r) <
(r) < (b'). Insa b'=bu, cu u element inversabil in A
si deci avem ca a=buq+r si ca
(b'). Insa b'=bu, cu u element inversabil in A
si deci avem ca a=buq+r si ca  '(r)
'(r) 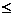
 (r) <
(r) < (b')=
(b')=  '(b), daca r
'(b), daca r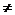 0.
0.
Pentru
a verifica pe i), observam ca din modul in care s-a definit  ' rezulta ca pentru a asociat cu a' avem
' rezulta ca pentru a asociat cu a' avem  '(a)=
'(a)=  (a'). Sa presupunem acum ca a|b si a,b
(a'). Sa presupunem acum ca a|b si a,b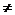 0.
Atunci, din faptul ca
0.
Atunci, din faptul ca  satisface ii)
si din demonstratia teoremei 2, rezulta ca idealul aA este
ideal principal generat de un element a', cu proprietatea ca a'
satisface ii)
si din demonstratia teoremei 2, rezulta ca idealul aA este
ideal principal generat de un element a', cu proprietatea ca a'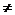 0,
0,  (a')
(a') 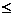
 (c) pentru orice c
(c) pentru orice c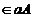 . Dar din aA=a'A
rezulta ca a si a' sunt asociate, deci
. Dar din aA=a'A
rezulta ca a si a' sunt asociate, deci  '(a)=
'(a)=
 (a'), de unde
(a'), de unde  '(a)=
'(a)=  (a')
(a') 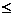
 '(b), pentru orice element asociat cu b este idealul
aA.
'(b), pentru orice element asociat cu b este idealul
aA.


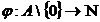 functia
respectiva si I un ideal in A. Vom arata ca I este ideal
principal. Daca I=(0), afirmatia este evidenta. Daca I
functia
respectiva si I un ideal in A. Vom arata ca I este ideal
principal. Daca I=(0), afirmatia este evidenta. Daca I