Fie K(=R) un corp
comutativ si (V, +) un grup abelian. Spunem ca V este K-spatiu vectorial daca
este definita o operatie algebrica
externa pe V, notata tot multiplicativ:
".": K x V 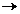 V, (a,x)=ax,
astfel incat sa fie indeplinite urmatoarele conditii: V, (a,x)=ax,
astfel incat sa fie indeplinite urmatoarele conditii:
i)
(a+b)x=ax+bx 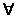 a,b a,b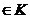 , ,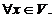
ii)
a(x+y)=ax+ay, 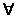 a a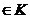 , ,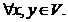
iii)
a(bx)=(ab)x,
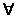 a,b a,b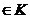 , ,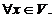
iv)
1x=x, 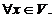 Elementele din K
se numesc scalari iar cele din V se numesc vectori. Elementele din K
se numesc scalari iar cele din V se numesc vectori.
Exemple.
Fie R2=. R2 este spatiu vectorial
peste R in raport cu operatiile:
"+"":
(a, b)+(c, d)=(a+c, b+d);
"."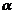 (a,b) = (a,b) =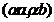 .
2.R3=. R3 este spatiu vectorial
peste R in raport cu operatiile: .
2.R3=. R3 este spatiu vectorial
peste R in raport cu operatiile:
"+"":
(a, b, c)+(d, e, f)=(a+d, b+e, c+f);
"."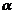 (a,b,c) = (a,b,c) =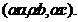
Definitie.
Fie V un spatiu vectorial peste corpul K. Fie 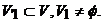 V1 se numeste subspatiu vectorial al spatiului
vectorial V daca V1 se numeste subspatiu vectorial al spatiului
vectorial V daca
i)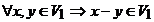 ; ;
ii) 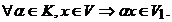 Notam acest lucru prin Notam acest lucru prin 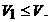
Exemplu. Avem R2
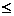 R3. R3.
Definitie. Fie V un K-spatiu vectorial si S= un sistem de n
vectori din V.
i) Spunem
ca S este un sistem liniar independent daca din orice relatie de forma a1x1+.+anxn=0
rezulta a1=.=an=0,
pentru orice i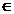 . Suma a1x1+.+anxn
se numeste combinatie liniara a elementelor x1,..,xn cu coeficienti din corpul K. . Suma a1x1+.+anxn
se numeste combinatie liniara a elementelor x1,..,xn cu coeficienti din corpul K.
ii) Daca exista
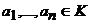 nu toate nule astfel
incat a1x1+.+anxn=0
spunem ca sistemul S este liniar dependent. nu toate nule astfel
incat a1x1+.+anxn=0
spunem ca sistemul S este liniar dependent.
iii) Sistemul
S formeaza sistem de generatori
pentru spatiul vectorial V daca pentru orice vector 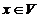 exista scalarii exista scalarii 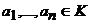 asatfel incat x= a1x1+.+anxn. asatfel incat x= a1x1+.+anxn.
iii) Sistemul
S formeaza o baza in spatiul
vectorial V daca este in acelasi
timp sistem de generatori si formeaza sistem de vectori liniar independenti.
Un spatiu vectorial poate avea mai multe baze, dar numarul vectorilor dintr-o
baza este mereu acelasi si se numeste dimensiunea
spatiului vectorial V.
Exemplu.
Sa se
arate ca vectorii x1=(1, 5, 2), x2=(-1, 1, 0), x3=(2, 1,
5) formeaza baza in R3.
Rezolvare. Verificam liniar independenta. Formam
combinatia liniara a1x1+a2x2+a3x3=0
si obtinem sistemul omogen 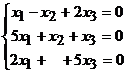 . Deoarece determinantul sistemului este 24, rezulta ca
sistemul omogen are doar solutia nula, deci vectorii sunt liniar
indepenedenti. . Deoarece determinantul sistemului este 24, rezulta ca
sistemul omogen are doar solutia nula, deci vectorii sunt liniar
indepenedenti.
Aratam
ca formeaza sistem de generatori. Fie x=(a,
b, c)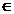 R3. Verificam
daca exista scalarii x1, x2,
x3 astfel incat R3. Verificam
daca exista scalarii x1, x2,
x3 astfel incat 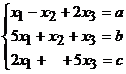 . Sistemul este de tip Cramer, decia admite solutie unica.
Deci sistemul formeaza sistem de generatori. . Sistemul este de tip Cramer, decia admite solutie unica.
Deci sistemul formeaza sistem de generatori.
Rezulta
ca formeaza baza.
|


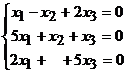 . Deoarece determinantul sistemului este 24, rezulta ca
sistemul omogen are doar solutia nula, deci vectorii sunt liniar
indepenedenti.
. Deoarece determinantul sistemului este 24, rezulta ca
sistemul omogen are doar solutia nula, deci vectorii sunt liniar
indepenedenti.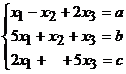 . Sistemul este de tip Cramer, decia admite solutie unica.
Deci sistemul formeaza sistem de generatori.
. Sistemul este de tip Cramer, decia admite solutie unica.
Deci sistemul formeaza sistem de generatori.