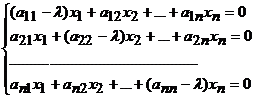Fie V un spatiu vectorial peste corpul comutativ K si f: V V o aplicatie liniara, cu dimV=n. Un vector x V o aplicatie liniara, cu dimV=n. Un vector x V- se numeste vector
propriu al aplicatiei liniare f daca exista V- se numeste vector
propriu al aplicatiei liniare f daca exista 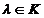 astfel ca f(x)= astfel ca f(x)=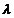 x. Scalarul x. Scalarul 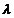 se numeste valoare proprie a aplicatiei liniare
f corespunzatoare vectorului
propriu x. se numeste valoare proprie a aplicatiei liniare
f corespunzatoare vectorului
propriu x.
Fie A=(aij)ij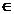 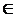 Mn(K), matrice
patratica de ordin n
cu coeficienti in corpul comutativ K si X Mn(K), matrice
patratica de ordin n
cu coeficienti in corpul comutativ K si X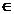 Mnx1(K). Daca exista Mnx1(K). Daca exista 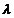 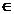 K astfel incat AX= K astfel incat AX=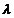 X, atunci X se numeste vector propriu al matricei A
, iar X, atunci X se numeste vector propriu al matricei A
, iar 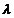 se numeste valoare
proprie pentru matricea A. Multimea
S se numeste valoare
proprie pentru matricea A. Multimea
S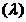 ={ ={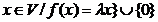 este subspatiu vectorial al patiului vectorial V si se
numeste subspatiu propriu
corespunzator valorii proprii este subspatiu vectorial al patiului vectorial V si se
numeste subspatiu propriu
corespunzator valorii proprii 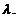
Fie In matricea unitate de ordin n, In 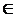 Mn(K). Atunci, cu
notatiile de mai sus, ecuatia matriceala AX= Mn(K). Atunci, cu
notatiile de mai sus, ecuatia matriceala AX=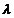 X devine ( A- X devine ( A-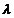 In) X=0 si este echivalenta cu sistemul liniar omogen: In) X=0 si este echivalenta cu sistemul liniar omogen:
 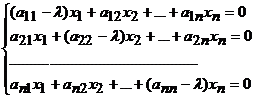 , ,
care are solutii nebanale
daca si numai daca det(A-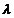 In)=0. Polinomul PA( In)=0. Polinomul PA(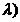 =det(A- =det(A-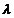 In) se numeste polinom
caracteristic al matricei A iar ecuatia det(A- In) se numeste polinom
caracteristic al matricei A iar ecuatia det(A-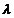 In)=0 cu In)=0 cu 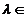 K se numeste ecuatia
caracteristica a matricei A. K se numeste ecuatia
caracteristica a matricei A.
Putem concluziona ca
valorile si vectorii proprii ai unei aplicatii liniare sunt valorile si
vectorii proprii ai matricei sale
asociate intr-o baza data.
|