CORELATIA
- PROBLEME
0,11
valoarea obtinuta de noi este 0,11 < 0,576
(corelatia este mai mare decat 5% din cazuri
nu ne putem exprima, suspendam decizia)
daca aveam rezultatul de 0,630 ne putem asuma decizia ca
este mai mic decat pragul de risc de 5%.
PROBLEMA 2
Unui grup de subiecti i se administreaza o
proba; o parte sunt respinsi, o parte sunt admisi (cu note
(rezultate) de la 1 la 10)
|
 rezultat test rezultat test
rezultat. examen
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
T
|
|
respinsi
|
|
4
|
9
|
15
|
10
|
5
|
1
|
|
|
|
44
|
|
admisi
|
1
|
0
|
1
|
2
|
9
|
15
|
18
|
13
|
5
|
3
|
67
|
|
Total:
|
1
|
4
|
10
|
17
|
19
|
20
|
19
|
13
|
5
|
3
|
11
|
T
Varianta continua: de la 1 - 10 - notele de la test
T
Varianta dihotomica: admis / respins
T
Numarul de subiecti > 50
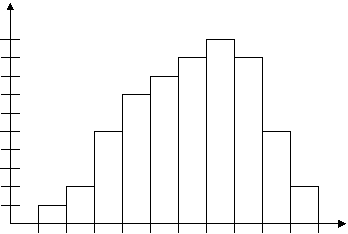
Variabila continua trebuie sa prezinte distributie normala (notele
de la test) pentru toti
subiectii - se observa o tendinta de simetrie.
20
18
16
14
12
10
8
6
4
2
1 2 3 4 5 6 7 8 9 10
distributie asimetrica
p = 44 /111 = 0,397
q = 67 / 111 = 0,603
q = 1 - p (x - f)
m' = 4,13 (respinsi) m' = 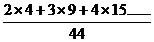
m' = 6,74 admisi
In tabel exista valori pana la 0,5
Valoarea noastra mai mica este 0,397
din tabel raportul pq/y = 0,6209
r.bis = 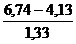 × 0,6209 = 0,83
trebuie interpretat
× 0,6209 = 0,83
trebuie interpretat
s = 1,33 (sa calculam acasa s - abaterea
standard)
Pentru interpretarea coeficientului de corelatie
biserial se calculeaza o eroare tip (gradul de eroare (estimare)
Eroarea tip:
E = 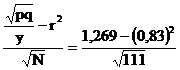 = 0,055
= 0,055
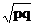

 /y - se ia din tabel
/y - se ia din tabel
0,055 = cat este eroarea pe care am comis-o cand am
calculat coeficientul biserial de corelatie
(patratul coeficientului de corelatie ne
arata cat)
Interpretare (0,83)2 = ~65% - proba este buna
predictia criteriului
PROBLEMA 3
COEFICIENTUL
ENEAHORIC (se
prezinta in 3 categorii)
Studiul relatiei dintre nivelul
stresului perceput la o clasa de elevi si nivelul
agresivitatii
Evaluarea pentru fiecare elev a fost facuta pe o
scala care indica:
stresul: -1: scazut
0: mediu
+1: ridicat
agresivitatea: -1: scazuta
0: medie
+1: ridicata
(valoarea medie intre m s
|
 nivel stres nivel stres
agresivitate
|
-1
|
0
|
+1
|
|
|
+1
|
13 n4
|
20
|
27 n1
|
D = 13 + 27 = 40
|
|
0
|
8
|
14
|
11
|
|
|
-1
|
6 n3
|
7
|
8 n2
|
C = 6 + 8 = 13
|
|
B = 13 + 6 = 19
|
|
A = 27 + 8 = 35
|
N = 114
|
Interpretare:
r = 0,16
N = 114
df. = 114 - 2 = 112 (in tabele pana la 100)
|
  p p
df
|
0,05
|
0,02
|
0,01
|
|
100
|
0,19
|
0,23
|
0,25
|
r = 0,16 - suspendam decizia
COEFICIENTI
NEPARAMETRICI
PROBLEMA 4
COEFICIENTUL j
cand cele 2 variabile sunt dihotomice prin natura lor si nu
dupa o regrupare
variabila trebuie sa indice prezenta sau absenta unei caracteristici, se noteaza
cu + sau -, 0 si 1.
Intr-o cercetare care sa vizeze relatia dintre
initiativa si promptitudine, avem un lot de 100 de
subiecti, sa se stabileasca relatia dintre
initiativa si promptitudine (2 variabile dihotomice prin natura
lor)
N = 100
I = 42 - initiativa =
y (b)
P = 29 = promptitudine = x (a)
I + P = 12 (si
initiativa si promptitudine) (c)
|
 y y
x
|
0
|
1
|
|
|
|
1
|
a
|
b 12 (c)
|
29 (a)
|
0 = absenta
|
|
0
|
c
|
d
|
|
1 = prezenta
|
|
|
42 (b)
|
|
|
frecvente relative sau proportii: 42%
initiativa, 29% promptitudine, 12% I+P
j = 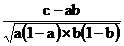 =
= 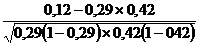 = .
= .
Tema
pentru acasa: Sa calculam:
c2
= 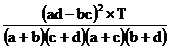 0
- absenta, 1 - prezenta
0
- absenta, 1 - prezenta
|
 y y
x
|
0
|
1
|
|
|
1
|
a 17
|
b 12 (c)
|
(a) =29 = a + b
|
|
0
|
c 41
|
d 30
|
71 = c + d
|
|
a+c = 58
|
b + d = 42 (b)
|
T = 100
|
j = 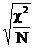
PROBLEMA 5
COEFICIENTUL DE
CORELATIE A RANGURILOR SPEARMAN r
In invatamant, cautam sa
vedem daca exista o relatie intre evaluarea facuta de
corpul didactic si autoapreciere. Scopul este de a se evidentia
gradul de obiectivitate al elevilor.
x: evaluare profesori: A B C D E F G H I K L M
1 2 3 4 5 6 7 8 9 10 11 12
y: autoevaluarea: C D A K B H L E G F M I
1 2 3 4 5 6 7 8 9 10 11 12
(literele inlocuiesc numele copiilor)
clasa medie: datele sub forma de clasamente: mai putin
de 30
Pasi:
1)
Decidem ce coeficient de corelatie folosim
2)
r = 1 - 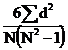 r
ia valori intre -1 si +1 (ca si r)
r
ia valori intre -1 si +1 (ca si r)
Atribuim rangurile (cifrele)
|
Subiecti:
|
x
|
y
|
dif.
|
ad2
|
|
1
|
1
|
3
|
-2
|
4
|
|
2
|
2
|
5
|
-3
|
9
|
|
3
|
3
|
1
|
-2
|
4
|
|
4
|
4
|
2
|
-2
|
4
|
|
5
|
5
|
8
|
-3
|
9
|
|
6
|
6
|
10
|
-4
|
16
|
|
7
|
7
|
9
|
-2
|
4
|
|
8
|
8
|
6
|
2
|
4
|
|
9
|
9
|
4
|
5
|
25
|
|
10
|
10
|
12
|
-2
|
4
|
|
11
|
11
|
7
|
4
|
16
|
|
12
|
12
|
11
|
1
|
1
|
|
N=12
|
|
|
|
100=ad2
|
r = 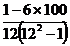 = 0,650, d = x - y
= 0,650, d = x - y
Coeficientul de corelatie r
Spearman se transforma in coeficientul 'r' - tabele de
echivalare
PROBLEMA 6
COEFICIENTUL DE
CONCORDANTA KENDALL
permite corelarea concordantei intre mai multe clasamente ale
acelorasi obiecte sau subiecti
ne spune cat de fidele sunt masuratorile facute (in
ce masura se acorda rangurile intre ele)
|
 subiecti subiecti
observator
|
A
|
B
|
C
|
D
|
E
|
|
|
M
|
2
|
1
|
3
|
4
|
5
|
|
|
N
|
1
|
2
|
4
|
5
|
3
|
|
|
P
|
5
|
3
|
4
|
1
|
2
|
|
|
Q
|
2
|
3
|
4
|
5
|
1
|
|
|
R
|
2
|
4
|
3
|
1
|
5
|
|
|
S
|
3
|
4
|
5
|
1
|
2
|
|
|
T
|
4
|
3
|
2
|
1
|
5
|
|
|
Rj
|
19
|
20
|
25
|
18
|
23
|
105 = a Rj
|
coeficientul ne spune cat de fidele sunt masuratorile
sau evaluarile facute
Avem 5 subiecti evaluati de 7 observatori; N = 5
(nr. subiecti)
S = 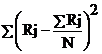 , unde Rj = suma rangurilor acordate fiecarui subiect
, unde Rj = suma rangurilor acordate fiecarui subiect
aRj = 105, 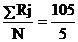 = 21
= 21
|
Rj - 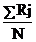
|
-2
(19-21)
|
-1
(20-21)
|
4
(25-21)
|
-3
(18-21)
|
2
(23-21)
|
T S
= 4 + 1 + 16 + 9 + 4 = 34 se
raporteaza la un tabel special
(-2)2 (-1)2 (+4)2 (-3)2 (2)2
W = 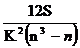 W
=
W
= 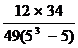


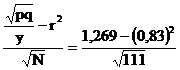 = 0,055
= 0,055



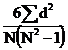
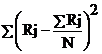 , unde Rj = suma rangurilor acordate fiecarui subiect
, unde Rj = suma rangurilor acordate fiecarui subiect