Categorii carteziene inchise
In teoria categoriilor, o categorie de cartezian
este inchisa daca, relativ vorbind, orice morfism definit pe
un produs de doua obiecte poate fi identificat cu un firesc morphism
definit pe unul din factori. These categories are
particularly important in mathematical logic and the theory of programming , in that they provide a natural setting for lambda calculus . Aceste categorii sunt
deosebit de importante in logica matematica si teoria de programare in
care acestea prevad o setare naturala pentru  -calcul. For generalizations of this notion to monoidal categories , see closed monoidal category .
-calcul. For generalizations of this notion to monoidal categories , see closed monoidal category .
Categoriile
carteziene inchise sunt un tip din
categorie formala are aceeasi
putere expresiva ca  -calcul. In sectiunile 1 si 2, vom defini aceste
notiuni si vom prezenta cateva din
-calcul. In sectiunile 1 si 2, vom defini aceste
notiuni si vom prezenta cateva din
proprietatile lor. In sectiunea 3 vom descrie conceptul de  -calcul. Sectiunea 4 descrie
-calcul. Sectiunea 4 descrie
constructii implicate in traducerea de la un formalism la altul, fara dovada.
Categoriile de produse carteziene inchise considerate in stiinta
calculatoarelor satisfac o proprietate puternica, adica 'a fi inchise cartezian' la nivel local,
inseamna ca fiecare parte din categorie
este inchisa cartezian.
Categorii carteziene inchise
Functii
de doua variabile
Daca S si T sunt doua seturi, apoi
un element din S×T poate fi vizualizat ca o pereche de elemente, unul din S
si celalalt din T, sau ca un singur element al produsului. Daca V
este un alt set, fie functia  poate fi privita ca o
functie de o singura variabila variind pe S×T sau ca o
functie de doua variabile, una din S si una de la T. Conceptual, noi
trebuie sa distingem intre aceste doua puncte de vedere, dar ele sunt
echivalente.
poate fi privita ca o
functie de o singura variabila variind pe S×T sau ca o
functie de doua variabile, una din S si una de la T. Conceptual, noi
trebuie sa distingem intre aceste doua puncte de vedere, dar ele sunt
echivalente.
Intr-o categorie mai
generala, notiunea de functie de doua variabile ar trebui
sa fie inteleasa ca o sageata al carui domeniu
este un produs. In anumite conditii, o astfel de functie poate fi
transformata intr-o functie de o
variabila, cu valori in functia 'obiect'. Ne vom indrepta atentia asupra acestui fenomen.
O functie de
doua variabile se poate transforma intr-o functie de o variabila al carei valori
sunt functii de o variabila. Mai precis, fie S, T si V sunt seturi si  o functie.
o functie.
Fie [S→ T] repezentand un set de
functii de la S la T. Apoi, fie functia 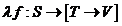 unde
unde  va fi o functie care va avea volorile
va fi o functie care va avea volorile 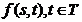 .Trecerea de la f la
.Trecerea de la f la 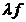 este numit currying .
este numit currying .
Un exemplu ar fi definitia functorului  dintr-un monoid care
prin currying se obtine
dintr-un monoid care
prin currying se obtine 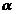 ..In alta directie, daca
..In alta directie, daca  este o functie,
va induce
este o functie,
va induce  definita prin
definita prin

Aceasta
constructie pentru a produce un invers  caredetermina un izomorfism
caredetermina un izomorfism
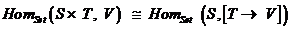
Aceste constructii pot fi usor de
recunoscut in limbaj categoric. Rezultatul acestei teorii este echivalent la  -calcul si are multe avantaje.
-calcul si are multe avantaje.
Definitie
Fie C o categorie se numeste o
categorie cartezian inchisa daca
satisface urmatoarele afirmatii:
exista un obiect 1.
fiecare pereche de obiecte A
si B din C este un produs A×B cu proiectiile
 si
si 
Vom presupune ca C va avea produse finite
si am uitilizat doua proiectii  si
si 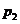 pentru un produs binar.
Vom utiliza acum
pentru un produs binar.
Vom utiliza acum
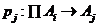
pentru j = 1, . ,n pentru a desemna j proiectii
din n produse.Aceasta utilizare nu ar trebui sa conflict cu exemplele
anterioare utilizate, deoarece am prezentat clar care va fi domeniu.
Propozitie In orice categorie de
produse carteziene inchise, pentru orice obiecte  si pentru orice
i=1,..,n va fi un obiect
si pentru orice
i=1,..,n va fi un obiect 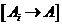 si functia
si functia
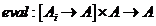
Daca pentru orice 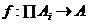 va fi o unica functie
va fi o unica functie
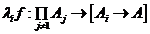
astfel incat diagrama urmatoare sa comute
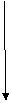

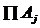


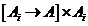 A
A
In Set, 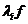 sunt functii de la
sunt functii de la
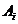 la A pentru fiecare
(n-1) - uplu
la A pentru fiecare
(n-1) - uplu

Fie A
si B doua obiecte fixate intr-o categorie de produse carteziene inchise si 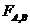 denota functorul Hom(-
× A,B), astfel incat g : D → C,
denota functorul Hom(-
× A,B), astfel incat g : D → C, 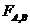 (g) : Hom(C×
A,B) → Hom(D×A,B) va lua f : C ×A →B in f
(g) : Hom(C×
A,B) → Hom(D×A,B) va lua f : C ×A →B in f  (g × A).
(g × A).
Rezulta ca
o categorie de produse finite poate fi o
categorie cu produse carteziene inchise doar daca adjunctii sunt unici.
Propozitie Fie C o categorie de produse finite .
Presupunem ca pentru fiecare pereche de obiecte A si B, sunt obiecte
[A → B] si [A→B]', eval: [A→B] × A→B si eval':
[A
→B]'× A→B. Presupunem aceste au proprietatea ca pentru orice functie
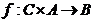 , impreuna cu functiile unice
, impreuna cu functiile unice
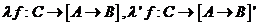
pentru ficare
 .
.
Apoi, pentru toate obiectele A si B,
exista o unica functie  , astfel incat pentru fiecare
, astfel incat pentru fiecare 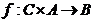 urmatoarele
diagrame sa comute:
urmatoarele
diagrame sa comute:
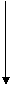
[A→B]'×A

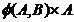
[A→B]×A
 [A→B]'
[A→B]'
C
[A→B]
 este un izomorfism.
este un izomorfism.
Exemple
Primul exemplu de categorie cartezian inchisa este categoria de
seturi. Pentru oricare doua seturi A si B, [A→B] este un set de
functii de la A la B, si 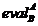
B este evaluarea sau functia aplicata. Retinem
ca, in cazul Set, [A→B] este
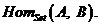
2. O algebra booleana B este un set partial ordonat , deci va corespunde
unei categorii C (B).Aceasta categorie este o categorie de produse
carteziene inchise. Obiectul final al algebrei B este 1, deci C(B) satisface conditia
1 din definitie. Deoarece B are minimul din oricare doua elemente, C(B) are
produse binare si am demonstrat conditia 2.
Pentru a dovedi conditia 3 vom defini
[a→b] pentru a fi  Pentru a demonstra
ca
Pentru a demonstra
ca
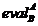 exita vom arata
ca exista
exita vom arata
ca exista  .Acest lucru se poate vedea din urmatorul calcul, care
utilizeaza legile distributive:
.Acest lucru se poate vedea din urmatorul calcul, care
utilizeaza legile distributive:

Existenta functiei  necesita sa
aratam ca atunci
necesita sa
aratam ca atunci 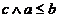 si
si  ( unicitatea lui
( unicitatea lui
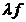 si faptul ca
si faptul ca 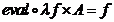 sunt automate, deoarece nu sunt Hom stabilite in categoria
determinata de catre un set partial ordonat care are mai mult de un
element). Fie urmatorul rezultat:
sunt automate, deoarece nu sunt Hom stabilite in categoria
determinata de catre un set partial ordonat care are mai mult de un
element). Fie urmatorul rezultat:
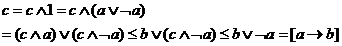
Un set partial ordonat finit care este categorie de produse carteziane
inchise
se numeste algebra Heyting.
Un algebra Heyting algebra este o generalizare a algebrei booleene. Algebrei
Heyting ii corespunde logica intuitionistica asa cum Algebrei booleene ii
corespunde logica clasica.Un
algebra Heyting este completa daca are sups? in toate subseturile.
O analiza aprofundata de proprietati elementare ale Algebrei
Heyting pot fi gasite in [Mac Lane si Moerdijk, 1992],
Un exemplu de categorie a caror obiecte sunt grafice si functiile
sunt homomorfsme de grafuri este de asemenea, cartezian inchisa. Daca
G si H sunt grafuri, atunci exponentiala [G H ] (care trebuie sa fie un graf) poate fi descrisa dupa cum
urmeaza. Fie NO un graf care contine un singur nod si fara sageti si AR graful cu o
sageata si doua noduri distincte, fiind nodurile sursa
si tinta din sageata.
Vom fixa doua
functii din NO in AR declarate astfel 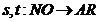 . Inca o data, faptul ca iau singur nod de la
sursa la tinta in graful AR. Apoi [G H ] este un graf care are ca seturi de noduri Hom (G ×NO,H ) din graful homomorfismelor de la G ×NO la H si setul de sageti este stabilit
de Hom (G ×AR,H ) cu functiile
sursa si tinta oferite de Hom (G ×s,H ) si Hom (G ×t,H ),
respectiv. Retineti ca, in cazul grafurilor, obiect [G H ] nu este un
set Hom (G H
. Inca o data, faptul ca iau singur nod de la
sursa la tinta in graful AR. Apoi [G H ] este un graf care are ca seturi de noduri Hom (G ×NO,H ) din graful homomorfismelor de la G ×NO la H si setul de sageti este stabilit
de Hom (G ×AR,H ) cu functiile
sursa si tinta oferite de Hom (G ×s,H ) si Hom (G ×t,H ),
respectiv. Retineti ca, in cazul grafurilor, obiect [G H ] nu este un
set Hom (G H
Deoarece [G H ] este un
obiect dintr-o categorie, trebuie sa fie un graf; dar
nici un set de obiecte nu este este Hom
(G H ). In special, pentru a
dovedi ca o categorie de
seturi cu structura carteziana nu este inchisa, nu este de ajuns sa demonstram
ca in incercarea de a pune o structura in Hom setul sa esueze.
5. Daca C este o categorie apoi Func (C; Set) este o categorie, obiectele sunt
functorii
si sagetile sunt transformarile naturale. Categoria Func (C; Set) este cartezian inchisa.
Daca F, G: C →Set sunt doi functori, F×G
produsul lor. Obiectul exponential [F →G] este tot functor. Pentru un
obiect C, [F →G] (C) este un set de
transformari naturale de la de functor Hom (C ; -) ×F la G. Pentru f : C → D o functie din C si 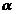 : Hom (C ;-) F → G o tranformare naturala, [F →G]
(f) (
: Hom (C ;-) F → G o tranformare naturala, [F →G]
(f) (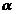 ) are in componenta un obiect A care va lua perechea
) are in componenta un obiect A care va lua perechea  cu
cu 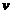 : D →A si
: D →A si  de la un element
de la un element  la G(A).
la G(A).
6. Categoria Cat ale micilor
categorii si functori este cartezian inchisa. In acest caz, pentru doua
categorii C si D C D] este
categoria ale caror obiecte sunt
functori de la C laD si a
caror sageti sunt transformari naturale intre ele. Daca F: B, C D este un functor, atunci  F: B C D] este functor definit in acest mod: daca B este un obiect din B, atunci pentru un obiect C din C,
F: B C D] este functor definit in acest mod: daca B este un obiect din B, atunci pentru un obiect C din C,  F (B ) (C ) = F (B ,C ) si, pentru o functie g: C→C',
F (B ) (C ) = F (B ,C ) si, pentru o functie g: C→C',  F (B) (g) este F (B,g): (B, C) →(B,C') din D. Pentru functia
f: B → B' din B,
F (B) (g) este F (B,g): (B, C) →(B,C') din D. Pentru functia
f: B → B' din B,  F (f) este transformare naturala de la
F (f) este transformare naturala de la  F (B) la
F (B) la  F (B') cu componentele
F (B') cu componentele  F (f) (C) = F (f; C), la un obiect C din C. Este instructiv
pentru a verifica faptul ca acest lucru da o transformare naturala.
F (f) (C) = F (f; C), la un obiect C din C. Este instructiv
pentru a verifica faptul ca acest lucru da o transformare naturala.
7. (Pentru cei familiarizati cu comenzi
complet partiale.) Categoria care contine  -CPOs -
-CPOs -
si functiile sunt continue este o catgeorie cartezian inchisa, desi
subcategoria stricta al  - CPOs nu este .Categoria
laticelor continue si a functiilor continue intre ele este cartezian
inchisa. Multe alte categorii de domenii au fost propuse pentru limbajul
de programare semantica, dar nu toate, sunt cartezian inchise.
- CPOs nu este .Categoria
laticelor continue si a functiilor continue intre ele este cartezian
inchisa. Multe alte categorii de domenii au fost propuse pentru limbajul
de programare semantica, dar nu toate, sunt cartezian inchise.
. Am descris modul de prezentare
al unui limbaj de programare functional ca o categorie.
Daca un astfel de limbaj este o categorie cartezian inchisa, atunci pentru
orice tip A si B, este [A →B] functii de la A la B. Se pot aplica programe de acest tip de date:
functii pot fi exploatate de catre programe. Aceasta inseamna
ca functiile sunt pe acelasi nivel ca alte
date, adesea descris prin a spune ca "functiile sunt primele clase de
obiecte'. Propunerea pune constrangeri puternice pentru a face din
functii prima clasa de obicete; daca veti face
anumite cerinte rezonabile pe tipuri [A →B], in esenta,
exista doar un mod de a face acest lucru.
Proprietati
ale categoriilor cartezian inchise
Multe din proprietati sunt consecintele unor
teoreme privind adjunctii. Vom prezenta acum cateva din proprietatile de baza
ale categoriilor
Avand in vedere f: B → C este o categorie cartezian inchisa intr-o
, avem compozite
[A →B]× A  C
C  C
C
Avand in vedere g: B →A vom avea
[A → C] ×B
Acestea vor fi utilizate in
urmatoarele propozitii
Fie A un obiect din categoria cartezian inchisa C
Exista functorii F: C C si G: C  C, pentru care
C, pentru care
(i) F(B) = [A→B] pentru oricare obiect B, si pentru orice functie f: B →C,
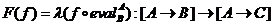
(ii) g(C) = [A→C] pentru oricare obiect C, si pentru orice
functie g: B →A
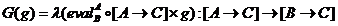
Valoarea lui F la f: B → C este in mod normal scris
[A
→ f]: [A → B] →[A → C]
si valoarea lui G la g: B →A este scris
[g
→ C]: [A→C]→[B→C]
Acestia sunt numiti Hom functori interni din categoria cartezian inchisa.
Vom dovedi ca F isi pastreaza
compozitia, pentru G este similar.
Noi trebuie sa aratam ca, pentru f:
B →C si g: C → D, [A → f]  [A →g] = [A → g
[A →g] = [A → g f].Prin definitie pentru orice h: X → Y, [A →h]
este unic, astfel incat urmatoarea diagrama sa comute:
f].Prin definitie pentru orice h: X → Y, [A →h]
este unic, astfel incat urmatoarea diagrama sa comute:
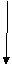
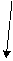
 [A→X]×A [A→Y]×A
[A→X]×A [A→Y]×A
eval
 X Y
X Y
In urmatoarea diagrama dreptunghiul exterior
va comuta astfel incat
[A→g] [A→f] = [A→g
[A→f] = [A→g  f].
f].


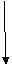
 [A→B]×A [A→C]×A [A→D]×A
[A→B]×A [A→C]×A [A→D]×A
eval

 B C D
B C D
In ceea ce priveste atat Hom (C×A,B) cat
si Hom (C, [A →B]) sunt priviti ca functori de oricare dintre cele trei variabile. Astfel pentru A si
B fixati , definim functorii
Hom (- A,B) si Hom ( -, [A →B]) care sunt functori natural
izomorfic.
Deoarece C×A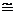 A×C si C, A pot fi tratate in acelasi mod ca
si C. Pentru A si C fixate definim functorii covarianti Hom (C×A ,
-) si Hom (C,[A → -]),.
A×C si C, A pot fi tratate in acelasi mod ca
si C. Pentru A si C fixate definim functorii covarianti Hom (C×A ,
-) si Hom (C,[A → -]),.
Teorema Functia  defineste un izomorfism natural
defineste un izomorfism natural
Hom(C×A,-)
→ Hom(C,[A→ -])
Propozitia de mai sus prezinta modul in care
[A→ - ] se comporta ca un Hom functor.
Propozitie
Urmatoarele izomorfisme se pastreaza pentru (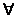 ) obiecte A, B si C in orice categorie cartezian
inchisa .Ultimele doua izomorfisme se pastreaza ori de cate ori obiectul initial sau suma
exista.
) obiecte A, B si C in orice categorie cartezian
inchisa .Ultimele doua izomorfisme se pastreaza ori de cate ori obiectul initial sau suma
exista.
(i) [A →1] 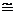 1.
1.
(ii) [1→A] 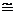 A.
A.
(iii) [A ×B→C] 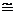 [A →[B →C]].
[A →[B →C]].
(iv [A→B]× [A→C] 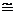 [A →B ×C].
[A →B ×C].
(v) [0 → A] 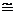 1.
1.
(vi) [A + B → C] 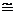 [A →C] ×[B →
C].
[A →C] ×[B →
C].
Este instructiv sa rescriem aceste izomorfisme utilizand notatia 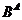 pentru obiectul [A →B].
pentru obiectul [A →B].
Aceste izomorfisme sunt " naturale in toate variabilele'. Apoi ambele
parti ale izomorfismului sunt functori din variabilele ramase intr-o maniera similara
cu propozitia de mai sus si va fi un izomorfism natural intre acesti
functori. Un exemplu, fie A si C fixate. Vom avea un izomorfism natural al
functorilor [A→-]×[A→C] si
[A →(- C)]. Avand in vedere f: B →B', [A →f] este ca o functie
si deci [A →f] ×[A → C], adica [A→f]×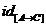 este produsul a doua functii,[A→(-C)] este definit in mod similar ca un compozitie
de functors.
este produsul a doua functii,[A→(-C)] este definit in mod similar ca un compozitie
de functors.
Fiecare din izomorfismele pot fi demonstrate prin utilizarea incluziunii Yoneda .
Vom demonstra (iii). Pentru B si C
doua obiecte fixate, vom avea functorul [- × B → C]
si
→[B → C]] de la C la C  . Apoi, avem urmatorul lant de
izomorfisme naturale.
. Apoi, avem urmatorul lant de
izomorfisme naturale.
Hom(1,[-
× B → C]) 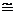 Hom( - × B, C)
Hom( - × B, C)
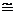 Hom(- , [B → C])
Hom(- , [B → C])
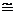 Hom(1,[- →[B → C]])
Hom(1,[- →[B → C]])
Propozitie
Fie C o categorie cartezian inchisa
cu obiectele A si B. Apoi,
 (eval) = id
(eval) = id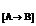 : [A → B] →[A → B]
: [A → B] →[A → B]
Prin eval ((
(( (eval))× A) = eval: [A → B] ×A →B din unicitate va
reiesi
(eval))× A) = eval: [A → B] ×A →B din unicitate va
reiesi
( (eval))× A = [A →B] ×A
(eval))× A = [A →B] ×A
(functia identitate), astfel incat primul
component a lui ( (eval)× A) trebuie sa fie identitatea.
(eval)× A) trebuie sa fie identitatea.
 -calcul
-calcul
In scopul de a
descrie conexiunea dintre categoriile cartezian inchise si  -calcul, vom da o scurta descriere a acestuia din urma.
Materialul este in esenta, adaptat de [Lambek si Scott, 1984]
si [Lambek si Scott, 1986].
-calcul, vom da o scurta descriere a acestuia din urma.
Materialul este in esenta, adaptat de [Lambek si Scott, 1984]
si [Lambek si Scott, 1986].
Definitie Un  -calcul este o teorie formala, constand in tipuri,
termeni, variabile si ecuatii. Pentru fiecare termen a,ii corespunde
un tip A, denumit "tipul lui a". Vom scrie
-calcul este o teorie formala, constand in tipuri,
termeni, variabile si ecuatii. Pentru fiecare termen a,ii corespunde
un tip A, denumit "tipul lui a". Vom scrie 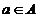 pentru a indica faptul ca a este un termen de tip A.
Acestea sunt supuse urmatoarelor
reguli:
pentru a indica faptul ca a este un termen de tip A.
Acestea sunt supuse urmatoarelor
reguli:
1) exista tipul 1.
2) Daca A si B sunt tipuri, atunci exista tipuri A×B si [A →B].
3) Exista un termen * de tip 1.
4) Pentru fiecare tip A, exista un set de termeni numarabili 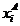 de tip A, denumite
variabilele de tip A.
de tip A, denumite
variabilele de tip A.
5) Daca a si b sunt termeni de
tip A si B,exista un termen (a,b) de tip A ×B.
6) Daca c este un termen de tip A×B, exista termenii proj (c) si proj
(c) si proj (c) de tip A si B,
(c) de tip A si B,
7) Daca a este un termen de tip A
si f este un termen de tip [A →B], atunci exista un termen f' de
tip B.
8) Daca x este o variabila de tip A si  (x) este un termen de
tip B, apoi
(x) este un termen de
tip B, apoi