PROIECT
DIDACTIC
Clasa :
a-XII-a
Obiectul :
Matematica - Algebra
Subiectul
lectiei : Inele - definitie, exemple
Tipul
lectiei : Lectie de dobandire
de noi cunostinte.
Conpetente
generale :
1. Folosirea terminologiei specifice matematicii in contexte variate de
aplicare.
2. Prelucrarea datelor de tip cantitativ, calitativ, structural sau
contextual, cuprinse in enunturi matematice.
3. Utilizarea algoritmilor si a conceptelor matematice in
rezolvarea de probleme.
4. Exprimarea si redactarea coerenta, in limbaj formal sau in
limbaj cotidian, a rezolvarii sau a strategiilor de rezolvare a unei
probleme.
5. Analiza de situatii - problema, in scopul descoperirii de
strategii pentru optimizarea solutiilor.
6. Generalizarea unor proprietati prin modificarea
contextului initial de definire a problemei sau prin generalizarea
algoritmilor.
Competente
specifice :
1. Identificarea proprietatilor operatiilor cu care este
inzestrata o multime.
2. Evidentierea asemanarilor si a deosebirilor
dintre proprietatile unor operatii definite pe multimi
diferite
3.1 Determinarea si verificarea proprietatilor
structurilor algebrice, inclusiv verificarea faptului ca o functie
data este morfism sau izomorfism.
4. Utilizarea proprietatilor operatiilor in calcule
specifice unei structuri algebrice.
5.1 Utilizarea structurilor algebrice in rezolvarea unor probleme de
aritmetica.
6.1 Transferarea, intre structuri izomorfe, a datelor initiale
si a rezultatelor, pe baza propriet
Strategia
didactica: activ-participativa.
Metode
si procedee didactice :conversatia euristica , exercitiul,
demonstratia, munca independenta.
Material
didactic utilizat : manual si culegere clasa a-XII-a , fise de lucru,
planse.
Tipuri
de actitati : frontala si individuala.
Procedee
de evaluare: analiza raspunsurilor, observarea sistematica a
atentiei ,verificarea cantitativa si calitativa a temei.
Scenariu
didactic:
1. Moment organizatoric: Verificarea prezentei elevilor si notarea
absentelor (daca sunt) in catalog. Asigurarea unei atmosfere
adecvate pentru buna
desfasurare a orei ;
2. Captarea atentiei: Verificarea temei elevilor prin sondaj
folosind dialogul profesor-elev ;elev-elev, prin confruntarea rezultatelor (in
cazul in care apar diferente se rezolva exercitiile la tabla ).
3. Informarea elevilor asupra
obiectivelor lectiei: Se anunta si se scrie pe tabla
titlul lectiei: Inele - definitie , exemple.
4. Prezentare de material nou
1. Definitie. Fie A o multime nevida si legile
de compozitie:
Tripletul 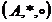 se numeste
inel daca sunt verificate axiomele
se numeste
inel daca sunt verificate axiomele
|
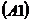
|
Axioma
grupului comutativ: Perechea 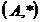 este grup
comutativ. este grup
comutativ.
|
|
|
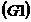 Axioma asociativitatii: Axioma asociativitatii:
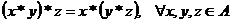
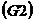 Axioma elementului neutru: Axioma elementului neutru:
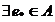 astfel
incat astfel
incat 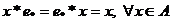
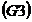 Axioma elementelor simetrizabile: Axioma elementelor simetrizabile:
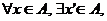 astfel incat astfel incat 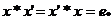
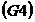 Axioma comutativitatii: Axioma comutativitatii:
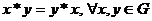
|
|
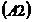
|
Axioma
monoidului: Perechea 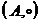 este monoid. este monoid.
|
|
|
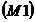 Axioma asociativitatii: Axioma asociativitatii:
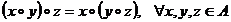
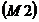 Axioma elementului neutru: Axioma elementului neutru:
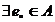 astfel incat astfel incat 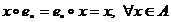
|
|
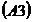
|
Axioma
distributivitatii:
|
|
|
 Legea " Legea " " este distributiva in raport cu legea "* ": " este distributiva in raport cu legea "* ":
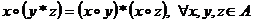
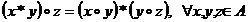
|
|
|
Inelul 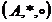 se
numeste inel comutativ daca legea de compozitie " se
numeste inel comutativ daca legea de compozitie " " este comutativa. " este comutativa.
|
|
|
|
|
|
|
|
|
|
Grupul 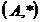 se numeste
grupul subiacent al inelului
se numeste
grupul subiacent al inelului 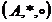 .
.
Prima operatie
a inelului se numeste adunare iar a doua operatie se numeste
inmultire.
Elementul
neutru al primei operatii se
numeste zeroul inelului 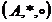 si se
noteaza
si se
noteaza 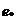 sau
sau 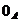 .
.
Simetricul
unui element 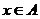 in grupul
subiacent
in grupul
subiacent 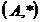 se numeste
opusul lui
se numeste
opusul lui 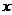 .
.
Elementul
neutru al celei de a doua oeratii
se numeste elementul unitate al inelului 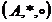 si se
noteaza
si se
noteaza 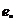 sau
sau 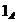 .
.
Elementele
simetrizabile ale monoidului 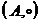 se numesc
elementele inversabile sau unitati ale inelului
se numesc
elementele inversabile sau unitati ale inelului 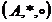 .
.
Multimea
unitatilor inelului 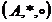 se noteaza
se noteaza 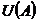 . Perechea
. Perechea 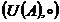 este un grup,
numit grupul unitatilor inelului
este un grup,
numit grupul unitatilor inelului 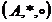 .
.
Exemple de
inele.
Din
proprietatile adunarii si inmultirii numerelor deducem
ca tripletele 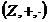 ,
, 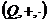 ,
, 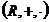 ,
, 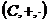 sunt inele
comutative.
sunt inele
comutative.
Avand in
vedere proprietatile adunarii si inmultirii
matricelor, rezulta ca tripletele 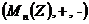 ,
, 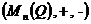 ,
, 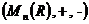 ,
, 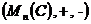 sunt inele
necomutative.
sunt inele
necomutative.
Elementul
nul in aceste inele este matricea nula 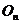 iar elementul
unitate este matricea unitate
iar elementul
unitate este matricea unitate 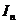 .
.
5.Consolidarea cunostintelor
si asigurarea feed-back-ului : Fiecare elev va primi cate o fisa
de lucru. Pe parcursul rezolvarii exercitiilor, profesorul intervine
cu intrebari ,adresate atat elevilor de la tabla cat si celor
din clasa, pentru a se clarifica demersul rezolvarii.
6.Tema pentru acasa : Se vor
propune spre rezolvare ca tema pentru acasa , exercitii din
fisa .
7.Aprecieri: se noteaza elevii care
s-au evidentiat in timpul orei.
Fisa
de lucru
Activitate
individuala.
Pe
multimea numerelor intregi se definesc legile de compozitie
a) Sa se studieze
daca 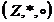 este inel
comutativ.
este inel
comutativ.
b) Sa
se determine grupul unitatilor inelului.
Exemple:
1) Inelul (Z,+, ) este
euclidian. Intr-adevar , in acest inel are loc teorema impartirii cu rest
pentru numere intregi , si anume:
a,bIZ , b q,rIZ a.i. a=bq+r . unde 0 r ¸| b|
.
Mai mult q si r sunt unice.
Considerind functia f: Z- N,
f(n)=| n |, rezulta clar ca inelul Z impreuna cu f este
euclidian (satisface conditiile 1 si 2). Mentionam ca teorema impartirii cu
rest la numere intregi o vom demonstra in paragraful 1 al capitolului III.
2) Orice corp este inel
euclidian. Intr-adevar, daca K este un corp, consideram functia f : K- N
definita prin f(a)=1, aIK ,a 0 . Aceasta functie satisface 1 si 2.
3) Inelul K[x] al polinoamelor
cu coeficienti intr-un corp K pentru care functia f :K[x] - N,
definita prin f(g)=grad(g), gIK[x] , g 0 , este un inel euclidian.
Intr-adevar, daca g,h IK[x], g 0 si g/h, atunci h=gg', cu g'IK[x],
deci grad(g)
grad(h), adica f(g) f(h). Deci conditia 1 este
indeplinita.
Sa verificam proprietatea 2. Fie f,gIK[x] cu g 0. Daca grad(g)=0, atunci f=g(g f),
deoarece g 0 din K, deci inversabil si afirmatia este
dovedita, adica este verificata proprietatea 2. Daca grad(g)>0, atunci vom
face o inductie dupa gradul lui f. Daca grad(f)<grad(g), in particular,
pentru grad(f)=0, din relatia f=g 0+f, rezulta 2.
Presupunem ca 2 afost verificata pent
434q1619e ru toate polinoamele f, cu grad(f)<n. Fie atunci f un polinom
de grad n, 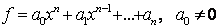 si g un polinom de gradul m,
si g un polinom de gradul m, 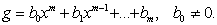 Putem presupune ca m n , conform celor demonstrate mai
sus. Atunci, polinomul
Putem presupune ca m n , conform celor demonstrate mai
sus. Atunci, polinomul 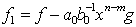 are gradul cel mult n-1, deoarece termenii de
gradul cel mai mare se reduc , deci grad(f1)<grad(f). Din ipoteza inductiva
rezulta, atunci ca exista q,rIK[x] a.i. f1=gq+r, unde r=0 sau
grad(r)<grad(g). Atunci avem:
are gradul cel mult n-1, deoarece termenii de
gradul cel mai mare se reduc , deci grad(f1)<grad(f). Din ipoteza inductiva
rezulta, atunci ca exista q,rIK[x] a.i. f1=gq+r, unde r=0 sau
grad(r)<grad(g). Atunci avem: 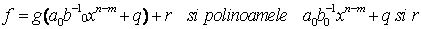 satisfac proprietatea 2. Polinoamele q si r IK[x] ,
numite citul si restul , astfel incit f=qg+r, r=0 sau grad(r)<grad(g); In cazul inelului K[x] sunt chiar
unice (ca si la Z , de altfel). Dar unicitatea acestora nu este necesara in
formula de impartire cu rest , in cazul inelului euclidian.
satisfac proprietatea 2. Polinoamele q si r IK[x] ,
numite citul si restul , astfel incit f=qg+r, r=0 sau grad(r)<grad(g); In cazul inelului K[x] sunt chiar
unice (ca si la Z , de altfel). Dar unicitatea acestora nu este necesara in
formula de impartire cu rest , in cazul inelului euclidian.
4) Inelul intregilor lui Gauss
este euclidian, in care functia din definitie este norma N. Definim pe Z[i]
functia f :Z[i] N, f(m+ni)=m +n (f(m+ni) este
patratul modulului numarului complex m+ni). Numarului complex z=a+bi, a,bIR, i se
asociaza in plan punctul M de coordonate (a,b). Numerele complexe din multimea
Z[i] sunt reprezentate in plan prin puncte ale caror coordonate sunt numere
intregi.
Reprezentindu-le , obtinem o retea in plan ca in figura 1. Consideram
z,z'IZ[i] , z' 0 si fie M punctul din plan asociat
numarului comlex z/z' . In retea exista un patrat ABCD in care se afla punctul
M. Fie A virful cel mai apropiat de M. Daca A(a,b) , atunci a,bIZ si A
este asociat numarului complex q=a+ib.
Pe de alta parte , cum latura patratului ABCD este unitate si cum A a
fost ales cel mai apropiat de M , obtinem ca distanta MA este mai mica decit
jumatate din diagonala patratului. Deci MA 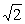 /2<1, dar MA este egal cu modulul numarului complex z/z'-q. Deci
avem: | z/z'-q|
/2<1, dar MA este egal cu modulul numarului complex z/z'-q. Deci
avem: | z/z'-q|
Avem,
atunci, |z-qz'|<|z'| si , notind r=z-qz', avem | r |<| z'| sau |
r |<| z'| si , deci, f(r)<f(z'). In concluzie, avem z=qz'+r, cu
f(r)<f(z') si, deci, Z[i] este inel euclidian. Din aceasta demonstratie
rezulta ca restul si citul impartirii nu sunt unic determinate.
 y
y





 B A
B A
M
 C D
C D

 x Fig.1.
x Fig.1.
Intr-adevar, daca M este centrul patratului ABCD, atunci putem alege
citul q al impartirii in egelitatea de mai sus , numarul complex q=a+ib, cu a,bIZ pentru
care (a,b) sa fie coordonatele oricaruia din virfurile patratului ABCD.
Sa exemplificam pe un
caz numeric ; consideram in Z[i] numerele
z=6i si z'=2+2i, pentru care z/z'=6i/(2+2i)=3/2+3i/2.
In figura 2 , punctul M , care este reprezentarea geometrica a
numarului comlex z/z'=3/2+3i/2, cade in centrul patrtului ABCD.
Deci putem alege citurile q1=1+i sau q2=2+i sau q3=2+2i sau q4=1+2i.
Avem egalitatile: z=z'q1+r1
unde r1=2i;
 z=z'q2+r1
unde r1=-2; y
z=z'q2+r1
unde r1=-2; y
z=z'q3+r1
unde r1=-2i;
z=z'q4+r1
unde r1=2.
In cele 4 cazuri , avem f(ri)<f(| z |), 1 i








 A(1,2) D(2,2) M(3/2,3/2) B(1,1) C(2,1)
A(1,2) D(2,2) M(3/2,3/2) B(1,1) C(2,1)

