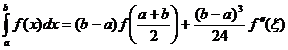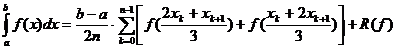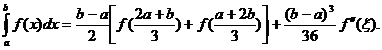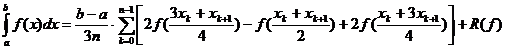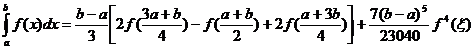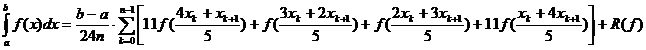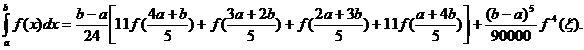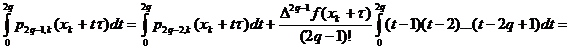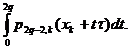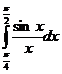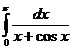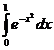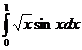Formulele
Newton-Cotes de tip deschis
Formulele
de integrare numerica deschise se obțin folosind polinoame de
interpolare pe noduri echidistante printre care nu se afla cel puțin
unul din capetele intervalului de integrare.
Daca h=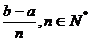 și x
și x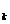 =a+kh,
=a+kh, 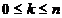 , atunci:
, atunci:
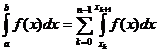 .
.
Pe fiecare
interval 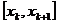 construim polinomul de
interpolare, de forma (12), al funcției f pe nodurile x
construim polinomul de
interpolare, de forma (12), al funcției f pe nodurile x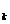 +i
+i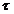 ,
, 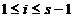 , cu
, cu 
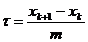 :
:
p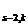 (x
(x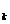 +t
+t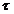 )=f(x
)=f(x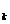 +
+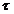 )+
)+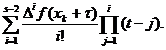
Pentru f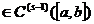 restul r
restul r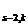 =f-p
=f-p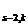 este:
este:
r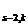 (x
(x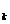 +t
+t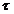
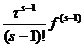 (C
(C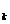 (t))
(t))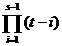 , (vezi formula (14)).
, (vezi formula (14)).
Folosind
un raționament asemanator celui din paragraful precedent pentru
obținerea formulelor (16), (18), obținem aici:
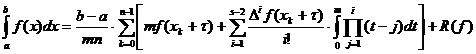
R(f)=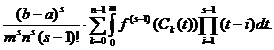
Cazuri particulare.
I. Pentru m=2, s=3 rezulta:
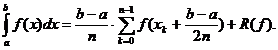
Deoarece 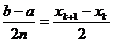 obținem formula:
obținem formula:
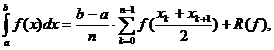 n
n ,
,
unde restul este:
R(f)=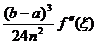
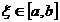
Pentru
n=1 rezulta:
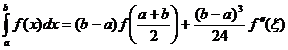
II. Pentru m=s=3 se obține
formula:
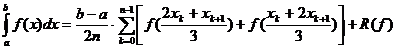
unde:
R(f)=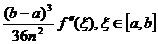
Daca n=1 atunci:
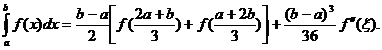
III. Pentru m=4, s=5 se obține formula:
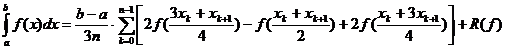
unde :
R(f)=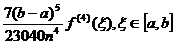
Pentru
n=1 avem:
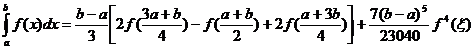
IV. Pentru m=s=5 rezulta formula:
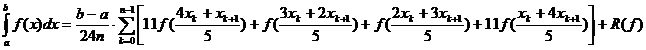 unde:
unde:
R(f)=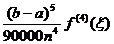
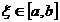
Pentru
n=1 avem:
Comentarii. 1 . In general, pentru m=2q vom lua s=2q+1, deoarece:
. In general, pentru m=2q vom lua s=2q+1, deoarece:
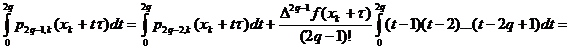
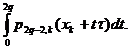
De aceea, și in acest caz, dintre
formulele Newton-Cotes deschise sunt preferate cele cu m par.
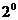 Comparand resturile din formulele
inchise și deschise, care folosesc același numar de noduri pe
fiecare subinterval
Comparand resturile din formulele
inchise și deschise, care folosesc același numar de noduri pe
fiecare subinterval 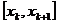 , vom constata ca pentru un numar de noduri de cel mult trei sunt
preferate cele de tip deschis (valoarea absoluta a restului este mai
mica). Pentru un numar de noduri in fiecare subinterval
, vom constata ca pentru un numar de noduri de cel mult trei sunt
preferate cele de tip deschis (valoarea absoluta a restului este mai
mica). Pentru un numar de noduri in fiecare subinterval 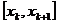 mai mare de patru, ordinul de
exactitate al celor inchise este mai mare.
mai mare de patru, ordinul de
exactitate al celor inchise este mai mare.
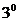 Modul de aplicare al acestor formule
este același cu cel folosit in paragraful precedent.
Modul de aplicare al acestor formule
este același cu cel folosit in paragraful precedent.
Exemple.
In tabelele
care urmeaza sunt trecute rezultatele obținute aplicand formula (37)
integralelor specificate in fiecare caz. Numarul 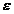 reprezinta diferența in
valoarea absoluta maxima admisa dintre doua
aproximații succesive.
reprezinta diferența in
valoarea absoluta maxima admisa dintre doua
aproximații succesive.

|
n
|
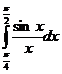
|
|
|
|
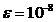
|
|
n
|
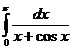
|
|
|
|
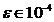
|
|
n
|
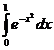
|
|
|
|
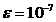
|
|
n
|
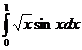
|
|
|
|
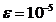
|


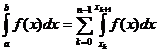 .
.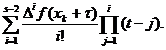
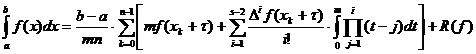
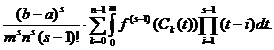
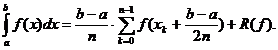
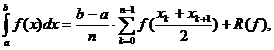 n
n